代数関数

数学において、代数関数（だいすうかんすう、英: algebraic function）は（多項式関数係数）多項式方程式の根として定義できる関数である。大抵の場合、代数関数は代数演算（英語版）（和、差、積、商、分数冪）のみでできる有限項の式に表すことができ、例えば

${\displaystyle f(x)=1/x,\;f(x)={\sqrt {x}},\;f(x)={\frac {\sqrt {1+x^{3}}}{x^{3/7}-{\sqrt {7}}\,x^{1/3}}}}$

などが典型的である。しかし、（エヴァリスト・ガロワとニールス・アーベルによって証明されたように）そのような有限表式に書けない代数関数もある。例えば、

${\displaystyle f(x)^{5}+f(x)^{4}+x=0}$

によって定義される関数がそのような例である。

代数関数を定義する多項式方程式の係数多項式として、有理数体 Q 上の多項式を考え、「Q 上代数的な関数」について述べることがかなり多い。そのような代数的関数を有理点において評価した値は代数的数を与える。

代数的でない関数は超越関数と呼ばれる。例えば、指数関数 ${\displaystyle \exp x}$、正接関数 ${\displaystyle \tan x}$、対数関数 ${\displaystyle \log x}$、ガンマ関数 ${\displaystyle \Gamma (x)}$ などが該当する。超越関数の合成が代数関数になることがある。例えば、${\displaystyle \cos(\arcsin x)={\sqrt {1-x^{2}}}}$ である。

定義

一変数代数関数

正確に言えば、一変数 x の次数 n の代数関数とは、ある多項式方程式

${\displaystyle a_{n}(x)y^{n}+a_{n-1}(x)y^{n-1}+\dotsb +a_{0}(x)=0}$

を満たす関数 y = f(x) である、ただし係数 a_i(x) は係数が適当な集合 S に属する x の多項式関数である。

n 次方程式は n 個の根を持つから、多項式方程式は陰伏的に、ただ 1 つの関数ではなく、n 個の関数（これらは分枝あるいは枝と呼ばれる）を定義する。例えば単位円の方程式 ${\displaystyle y^{2}+x^{2}=1\,}$ を考えよう。これは全体に渡る符号の違いのみを除けば y を決定するから、したがって 2 つの枝を持つ： ${\displaystyle y=\pm {\sqrt {1-x^{2}}}.\,}$

多変数代数関数

m 変数の代数関数は m + 1 変数の適当な多項式方程式

${\displaystyle p(y,x_{1},x_{2},\dots ,x_{m})=0}$

の解となる関数 y として同様に定義される。通常 p は既約多項式と仮定される。すると代数関数の存在は陰関数定理によって保証される。

形式的には、体 K 上の m 変数の代数関数は、有理関数体 K(x₁,...,x_m) の代数閉包の元である。

一変数の代数関数

導入と概観

代数関数のインフォーマルな定義は代数関数の性質について多くの手掛かりを与えてくれる。直感的な理解を得るために、代数関数を、通常の代数的演算（英語版）、すなわち和、積、商、n 乗根を取ることによって書くことのできる関数と見ることは、助けになるであろう。もちろん、これは簡略化し過ぎである。というのも、還元不能の場合 (casus irreducibilis)（英語版） によって（そしてより一般にガロワ理論の基本定理によって）、代数関数は冪根によって書けるとは限らないからである。

まず、任意の多項式関数 ${\displaystyle y=p(x)}$ が代数関数であることに注意する。これは単純に方程式

${\displaystyle y-p(x)=0}$

の解 y として書けることによる。より一般に、任意の有理関数 ${\displaystyle y={\frac {p(x)}{q(x)}}}$ は方程式

${\displaystyle q(x)y-p(x)=0}$

の解として代数関数になる。さらに、任意の多項式の n 乗根 ${\displaystyle y={\sqrt[{n}]{p(x)}}}$ は方程式

${\displaystyle y^{n}-p(x)=0}$

を解く代数関数である。驚くべきことに、代数関数の逆関数は代数関数である。各値の x に対して y が方程式

${\displaystyle a_{n}(x)y^{n}+\cdots +a_{0}(x)=0}$

の解となると仮定するならば、x は各値の y に対するこの方程式の解である。実際、x と y の役割を入れ替えて x に関して同類項をまとめれば

${\displaystyle b_{m}(y)x^{m}+b_{m-1}(y)x^{m-1}+\cdots +b_{0}(y)=0}$

と書きなおすことができるから、x を y の関数として書けば逆関数を得、これはまた代数関数である。

しかしながら、すべての関数が逆を持つわけではない。例えば、y = x² は horizontal line test を通過せず、単射でない。逆は代数"関数" ${\displaystyle x=\pm {\sqrt {y}}}$ である。これを理解する別の方法は、代数関数を定義する多項式方程式の枝全部の集合は代数曲線のグラフであるということである。

複素数の役割

代数的な観点から、複素数は極めて自然に代数関数の研究に入ってくる。まず、代数学の基本定理によって、複素数全体は代数閉体である。したがって多項式関係 p(y, x) = 0 は、y が複素数値を取ってよいとして、各点 x において y について少なくとも 1 つの解（そして一般に x についての p の次数を超えない個数の解）を持つことを保証される。したがって、代数関数の領域を処理する問題は安全に最小化することができる。

代数関数 y の 3 つの分枝のグラフ。ここに y³ − xy + 1 = 0 で、領域は 3/2^2/3 < x < 50.

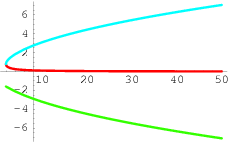
さらに、最終的には実の代数関数に興味があったとしても、複素数に頼らずに和、積、商、n 乗根を取ることによって関数を表す手段は存在しないかもしれない（casus irreducibilis 参照）。例えば、方程式

${\displaystyle y^{3}-xy+1=0\,}$

によって決定される代数関数を考えよう。三次方程式の解の公式（英語版）を用いて次を得る：

${\displaystyle y=-{\frac {2x}{\sqrt[{3}]{-108+12{\sqrt {81-12x^{3}}}}}}+{\frac {\sqrt[{3}]{-108+12{\sqrt {81-12x^{3}}}}}{6}}.}$

${\displaystyle x\leq {\frac {3}{\sqrt[{3}]{4}}}}$ に対して、平方根は実でありしたがって立方根は唯一の実根として問題なく定義される。一方、${\displaystyle x>{\frac {3}{\sqrt[{3}]{4}}}}$ に対しては、平方根は実でなく、実でない平方根のいずれかを選ばなければならない。そして立方根は 3 つの非実数の中から選ばなければならない。公式の 2 つの項において同じ選択がされれば、3 乗根の 3 つの選択は添付の画像のように 3 つの分枝を与える。

結果の関数は書かれているグラフの領域上実数値であるにもかかわらず実数のみを用いて n 乗根のことばで表すことは決してできないことを示すことができる。

より重要な理論的なレベルでは、複素数を用いることで複素解析の強力なテクニックを用いて代数関数を議論することができる。とくに、偏角の原理を用いて、任意の代数関数は実は少なくとも多価関数の意味で解析関数であることを示すことができる。

フォーマルに、p(x, y) を複素変数 x と y の複素多項式とする。x₀ ∈ C は y の多項式 p(x₀, y) が n 個の相異なる零点を持つようなものとする。代数関数が x₀ のある近傍で解析的であることを示そう。これらの零点のそれぞれを含む n 個の重ならない円板 Δ_i たちをとる。すると偏角の原理によって

${\displaystyle {\frac {1}{2\pi i}}\oint _{\partial \Delta _{i}}{\frac {p_{y}(x_{0},y)}{p(x_{0},y)}}\,dy=1.}$

連続性から、これは x₀ のある近傍内の任意の x に対しても成り立つ。とくに、p(x, y) は Δ_i においてただ 1 つの解を持ち、それは留数定理によって与えられる:

${\displaystyle f_{i}(x)={\frac {1}{2\pi i}}\oint _{\partial \Delta _{i}}y{\frac {p_{y}(x,y)}{p(x,y)}}\,dy}$

これは解析関数である。

一価性

上述の解析性の証明は x が p(x, y) の臨界点 (critical point) でない場合に n 個の相異なる関数要素 (function element) f_i(x) の系の表現を導出したことに注意しよう。臨界点とは相異なる零点の個数が p の次数よりも小さいような点のことであり、これは p の最高次の項が消えるところ、そしてその判別式が消えるところにおいてのみ現れる。したがってそのような点は高々有限個 c₁, ..., c_m しか存在しない。

臨界点の近くでの関数要素 f_i の性質を同じように解析することによって、モノドロミー被覆（英語版）は臨界点（と無限遠点でもよい）上分岐することを示すことができる。したがって f_i に伴う整関数は悪くとも臨界点上代数的な極と通常の代数的分岐を持つだけである。

臨界点から離れれば f_i たちは定義によって p の相異なる零点であるから

${\displaystyle p(x,y)=a_{n}(x)(y-f_{1}(x))(y-f_{2}(x))\cdots (y-f_{n}(x))}$

であることに注意しよう。モノドロミー群は因子を入れ替えることによって作用し、したがって p のガロワ群のモノドロミー表現 (monodromy representation) をなす。（普遍被覆空間上のモノドロミー作用は関連しているがリーマン面の理論における異なる概念である。）

歴史

代数関数に関係するアイデアは少なくともルネ・デカルトまでさかのぼる。代数関数の最初の議論はエドワード・ウェアリングの 1794 年の An Essay on the Principles of Human Knowledge にあるものだと思われる。そこで彼は次のように書いている。

“let a quantity denoting the ordinate, be an algebraic function of the abscissa x, by the common methods of division and extraction of roots, reduce it into an infinite series ascending or descending according to the dimensions of x, and then find the integral of each of the resulting terms.”

関連項目

• 解析関数
• 関数 (数学)
• 関数の種類の一覧（英語版）
• 初等関数
• 複素関数
• 多項式
• 超越関数
• 超関数
• 特殊関数
• 特殊関数とエポニム一覧（英語版）
• 有理関数
• 代数式

参考文献

• Ahlfors, Lars (1979). Complex Analysis. McGraw Hill
• van der Waerden, B.L. (1931). Modern Algebra, Volume II. Springer

外部リンク

• Definition of "Algebraic function" in the Encyclopedia of Math
• Weisstein, Eric W. "Algebraic Function". mathworld.wolfram.com (英語).
• Algebraic Function - PlanetMath.（英語）
• Definition of "Algebraic function" in David J. Darling's Internet Encyclopedia of Science