Remove ads
ファジィ論理（ファジィろんり、英: Fuzzy logic）は、1965年、カリフォルニア大学バークレー校のロトフィ・ザデーが生み出したファジィ集合から派生した[1][2]多値論理の一種で、真理値が0から1までの範囲の値をとり、古典論理のように「真」と「偽」という2つの値に限定されない[3]ことが特徴である。ファジィ論理は制御理論（ファジィ制御）から人工知能まで様々な分野に応用されている。
ファジィ論理と確率論理は数学的に似ており、どちらも0から1までの値を真理値とするが、概念的には解釈の面で異なる。ファジィ論理の真理値が「真の度合い」に対応しているのに対し、確率論理では「確からしさ」や「尤もらしさ」に対応している。このような違いがあるため、ファジィ論理と確率論理では同じ実世界の状況に異なるモデルを提供する。
真理値と確率が0から1の範囲の値をとるため、表面的には似ているように思われる。例えば、100mlのコップに30mlの水が入っているとする。これに対して「空」と「満杯」の2つの概念を考える。それぞれの意味は所定のファジィ集合、およびそれを定義付けるメンバシップ関数で表される。例えば、そのコップについて「空だ」が真である度合いは0.7、「満杯だ」が真である度合いは0.3と定義することも考えられる。「空だ」という概念は主観的であり、観察者や設計者によって感じ方は異なる。設計者によっては、50mlでも満杯だとするようにメンバシップ関数を設定するかもしれない。ファジィ論理ではあいまいな現象の数理モデルとして「真の度合い」を使うのに対し、確率論は未知のことに対しての数理モデルである。確率論的手法を使って同じことを達成するには、「満杯」か否かを表す二値変数をコップに入っている水の量という連続値によって決定するという形で定義することになる。
ファジィ論理の真理値の具体例
ファジィ論理は洗濯機や冷蔵庫のような家電機器の制御に使われる。例えば洗濯機では、洗濯物の量や洗剤の濃度を調べて、洗濯槽の回転などを調整する。
基本的な応用の特徴として、連続値をいくつかの区分に分ける点が挙げられる。例えば、アンチロック・ブレーキ・システムでは温度を測定するが、温度をいくつかの区分に分け、それぞれにメンバシップ関数を定義し、ブレーキを適切に制御する。各関数は同じ温度に0から1までの真理値を割り当てる。これらの真理値を使って、ブレーキをどう制御すべきかを決定する。
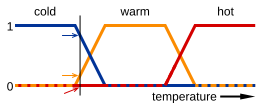
上図では、cold、warm、hot という関数で温度の値をマッピングしている。ある温度には各関数に対応した3つの真理値がある。上図で縦線で示している温度を見てみると、3つの真理値（0.8、0.2、0）が対応し、それらを解釈すると「かなり冷たい」（青い矢印）、「やや暖かい」（黄色の矢印）、「熱くない」（赤い矢印）ということになる。
言語学的変数
数学における変数は一般に数値を値とするが、ファジィ論理は非数値的な「言語学的変数」を使うことで規則や事実の表現が容易になるような分野にもよく応用される[4]。
ここでいう「非数値的」「言語学的」という意味は、例えば速度といったような変数のような「確定的な値を持つような変数」ではない、という意味であって、実際のところ（ソシュールやチョムスキーらによるような）言語学的な何かがあるわけではない。具体例として「年齢」に対し「若い」、あるいはその反対の「高齢だ」という値は、結局のところ、「20歳」という実際の年齢に対して、「若い」は 0.8 という高い値になり、「高齢だ」は 0.05 という低い値になる、といったように、最終的には実数（数値）になるのである。言語学的変数の最大の利点は、主たる単語に修飾語を添えることでその意味を修正できる点であると主張される。修飾語は特定の関数と対応付けることができる。例えば、ザデーはメンバシップ関数の平方をとることを提案している。
ファジィ論理の応用例
- ヴィークルの制御や群管理。オートマチックトランスミッション、アンチロック・ブレーキ・システム、クルーズコントロール。日本の鉄道車両では仙台市交通局1000系電車が初期の導入例として知られる。
- 空調
- CG合成ソフト(MASSIVEなど)
- カメラ
- デジタル画像処理（エッジ検出など）
- 炊飯器
- 食器洗い機
- エレベーター
- 洗濯機などの家電機器
- コンピュータゲームの人工知能
- 電子掲示板などで好ましくないテキストを排除するフィルタ
- リモートセンシングでのパターン認識
- マイクロコントローラやマイクロプロセッサ（Freescale 68HC12など）。
Remove ads
ファジィ集合論では、ファジィ集合に関するファジィ演算を定義している。これを利用する際の問題は、適切なファジィ演算がどれなのかわからない場合があることである。そのため、ファジィ論理ではIF/THEN規則やそれに類するもの（例えばファジィ関係行列）を使うのが一般的である。
規則は以下のような形式で表現される。
- IF 「変数」IS「集合」THEN 「アクション」を実行する。
例えば、ファンを使って温度を一定に保つ非常に単純な機器があるとしたら、次のような規則が考えられる。
- IF 温度 IS 「非常に寒い」 THEN ファンを止める。
- IF 温度 IS 「寒い」 THEN ファンを遅くする。
- IF 温度 IS 「普通」 THEN ファンを一定に保つ。
- IF 温度 IS 「暑い」 THEN ファンを速くする。
ELSE節がない点に注意されたい。全ての規則は同時に評価される。何故なら、温度は（程度の差はあっても）同時に「寒い」と「普通」の両方に属するといったことが考えられるからである。
ブール論理の論理演算 AND, OR, NOT に相当する演算がファジィ論理にもあり、例えば下記のように定義される。下記の定義はザデーのオリジナルの論文で定義されていたもので、ザデー演算子とも呼ばれる。ここで x と y はファジィ変数である。
- NOT x = (1 - truth(x))
- x AND y = minimum(truth(x), truth(y))
- x OR y = maximum(truth(x), truth(y))
他の演算として、より言語的な「ヘッジ（hedges）」がある。これは、数式で表される集合の意味（例えば「寒い」）を修飾する「非常に」とか「いくぶん」といった副詞に相当するものである。
プログラミング言語での応用として、Prologは規則群のデータベースに論理問い合わせを行う構造になっていて、ファジィ論理との相性が良い。このようなプログラミングを論理プログラミングという。
その他の例
身長を「高い」と「低い」に分けることを考える。古典集合論（古典論理）では、例えば次のように規則を定義する。
- 男の身長が1.8メートルなら、その人は背が高い。
- IF man IS true AND height >= 1.8 THEN is_tall IS true; is_short IS false
ファジィ規則は背が「高い」と「低い」を明確に区別しない。そのような区別は現実的ではない。そこで、以下のような規則を定義する。
- IF height <= medium male THEN is_short IS agree somewhat
- IF height >= medium male THEN is_tall IS agree somewhat
ファジィの場合、1.83メートルのような明確な身長の区分けはせず、次のようなファジィ値の割り当てをする。
- dwarf male = [0, 1.3] m
- short male = (1.3, 1.5]
- medium male = (1.5, 1.8]
- tall male = (1.8, 2.0]
- giant male > 2.0 m
従って、真理値も二値ではなく、以下のような5値にする。
- agree not = 0
- agree little = 1
- agree somewhat = 2
- agree a lot = 3
- agree fully = 4
クリスプ集合（二値）の場合、1.79メートルの身長の人は単に背が低いとされる。1.8メートルや2.25メートルの人は背が高いとされる。
なお上の記述では、性別を二値情報、すなわち既知で曖昧さのない情報とみなしている。対象の性別を外見などから判断する場合、もしくは間性の存在などを考慮する場合には、性別についてもファジィ値を導入し、規則の条件部を
IF male >= agree somewhat AND ...
のようにする必要がある。
Remove ads
数理論理学には、これまで説明してきたファジィ論理をモデルとして形式体系がいくつか存在する。その多くは、いわゆるt-normファジィ論理に属する。なお、各論理体系で使われる演算は前述のザデー演算子とは異なる場合がある。
命題ファジィ論理
主な命題ファジィ論理としては、以下のものがある。
- 基本命題ファジィ論理 BL は、論理積を連続な三角型ノルム(t-norm)で定義し、含意をt-normの残余として定義する公理化された論理である。そのモデルは BL-algebra と呼ばれる。三角型ノルムt(x,y)は以下の性質をもつ:
- 可換性:
- 結合性:
- 単調性:
- 単位元1:
- ウカシェヴィチ・ファジィ論理は、基本ファジィ論理の特殊ケースであり、論理積はウカシェヴィチt-norm()になっている。基本的な論理公理の他に二重否定の除去も公理とし（従って直観論理ではない）、そのモデルは MV-algebra と呼ばれる。
- ゲーデル・ファジィ論理は、基本ファジィ論理の特殊ケースであり、論理積はゲーデルt-norm()になっている。基本的な論理公理の他に論理積の冪等性も公理とし、そのモデルは G-algebra と呼ばれる。
- プロダクト・ファジィ論理は、基本ファジィ論理の特殊ケースであり、論理積はプロダクトt-norm()になっている。そのモデルは product algebra と呼ばれる。
- MTL（Monoidal t-norm logic）は、基本ファジィ論理を拡張したもの。
- Rational Ravelka logic は、多値論理を拡張したもの。ウカシェヴィチ・ファジィ論理の拡張でもある。
述語ファジィ論理
命題論理から一階述語論理が生成されるように、上述のファジィ論理に全称量化子と存在量化子を追加すると述語ファジィ論理となる。量化された論理式のファジィ真理値について、全称量化では下限、存在量化では上限を意味する。
ファジィ論理と決定可能性
「決定可能部分集合」や「帰納的可算部分集合」は古典数学と古典論理の基本である。すると当然ながら、ファジィ集合論にそれらを拡張するという問題が生じる。このような方向性の最初の提案は、E.S. Santos による「ファジィ・チューリングマシン」、「マルコフ正規ファジィアルゴリズム」、「ファジィ・プログラム」の提唱だった[5]。それに続いて L. Biacino と G. Gerla [6]がそれらの定義が適正でないことを示し、次のようなことを提案した。Ü は [0,1] の有理数の集合を意味する。
ファジィ集合 S のファジィ部分集合 s : S [0,1] が「帰納的可算」であるのは、帰納的写像 h : S×N Ü が存在する場合で、それはすなわち S の全ての x について関数 h(x,n) が n に対応して増加し、s(x) = lim h(x,n) となる場合である。s が「決定可能」であるのは、s とその補集合 –s が共に「帰納的可算」の場合である。Gerla 2006でL-部分集合の一般ケースでのこうした理論の拡張が示されている。提案されている定義はファジィ論理ともうまく整合している。実際、次の定理が成り立つ（ファジィ論理の推論機構が明らかな有効的特性を満たしているならば）。
- 定理
- どのような公理化可能なファジィ理論も帰納的可算である。一般に妥当な論理式のクリスプ集合が帰納的可算でないとしても、論理的に真である論理式のファジィ集合は帰納的可算である。さらに、公理化可能で完全な任意の理論は決定可能である。
ファジィ部分集合の帰納的可算性についての提案された観念が適正なものだとしても、ファジィ論理についてチャーチ＝チューリングのテーゼが成り立つかどうかは未解決の問題である。そのためには、ファジィ文法やファジィ・チューリングマシンのさらなる研究が必要である[7]。さらにその先にある未解決の問題として、ゲーデルの定理群のファジィ論理向けの拡張がある。
Remove ads
ファジィ関係が定義されれば、ファジィ関係データベースを開発することもできる。世界初のファジィ関係データベース FRDB は、Maria Zemankova が論文で発表した。その後 Buckles-Petry モデル、Prade-Testemale モデル、Umano-Fukami モデル、GEFREDモデルといったモデルも生み出されている。ファジィ・データベースという意味では、クエリのためのファジィ問い合わせ言語もいくつか定義されており、SQLf、FSQL などがある。これらはSQL文に、ファジィ的要素（ファジィ条件、ファジィ演算、ファジィ制約、ファジィ制限、ファジィしきい値、言語ラベルなど）を取り入れた構造を定義している。
ファジィ論理も確率も不確かさを別の方法で表現している。ファジィ論理も確率論も主観的信念を表現できるが、ファジィ集合論ではメンバシップの概念を使い、確率論ではベイズ確率の概念を使う。この区別は主に思想的なものだが、ファジィ論理に基づく確率測度は確率論の確率測度とは本質的に異なり、直接的に等価ではない。統計学者の多くはブルーノ・デ・フィネッティの業績を信じており、数学的不確かさを論じる理論は1つで十分であって、ファジィ論理は不要だと考えている。一方バート・コスコは、確率では一種類の不確かさしか表せないのだから、確率論がファジィ論理に包含されるとした。彼はまた、ファジィ集合論の概念からベイズの定理を導出できることを証明したと主張している。ファジィ論理を生み出したロトフィ・ザデーは、ファジィ論理は確率とは異なる性格を持つとし、確率を代替するものではないとした。彼は確率論の代替となる Possibility Theory も生み出している[8]。
Remove ads
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads