調和平均

数学において、調和平均（ちょうわへいきん、英: harmonic mean, subcontrary mean）とは、いくつかある広義の平均のうちの一つである。典型的には、率(割合・比率)の平均が望まれているような状況で調和平均が適切である。

正の実数について、調和平均は逆数の算術平均の逆数として定義される。例えば、3つの数 1, 2, 4 の調和平均は次のようになる：

${\displaystyle {\frac {3}{{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{4}}}}={\frac {1}{{\frac {1}{3}}({\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{4}})}}={\frac {12}{7}}.}$

定義

正の実数 x₁, x₂, …, x_n について、調和平均 H は

${\displaystyle H={\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}={\frac {n}{\sum \limits _{i=1}^{n}{\frac {1}{x_{i}}}}}={\frac {n\prod \limits _{j=1}^{n}x_{j}}{\sum \limits _{i=1}^{n}{\frac {\prod \limits _{j=1}^{n}x_{j}}{x_{i}}}}}}$

と定義される。これは逆数の算術平均の逆数であり、

${\displaystyle {\frac {n}{H}}=\textstyle \sum \limits _{i=1}^{n}\displaystyle {\frac {1}{x_{i}}}={\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}$

と書ける。

重み付き調和平均

重み（英語版）の集合 w₁, w₂, …, w_n が伴ったデータ集合 x₁, x₂, …, x_n について、重み付き調和平均 (weighted harmonic mean) を考えることができ、次で定義される：

${\displaystyle {\frac {\sum \limits _{i=1}^{n}w_{i}}{\sum \limits _{i=1}^{n}{\frac {w_{i}}{x_{i}}}}}}$

重み付き調和平均で重みがすべて 1 の特別な場合が、上で定義した（通常用いられる）調和平均である。重みがすべて等しい任意の集合に対する重み付き調和平均は、調和平均に等しい。

位置付け

調和平均は一般化平均（英語版）でパラメータを −1 とした特別な場合 (M₋₁) であり、また3つのピタゴラス平均の一つである。ピタゴラス平均の残る2つは算術平均 (M₁) と幾何平均 (M₀) である。

調和平均は、典型的には率や比に対する平均を考える場合に適切である。例えば速度の平均を計算することを考えると、乗り物がある距離を時速 60 km で走りそれから同じ距離を時速 40 km で走った場合、全体の走行時間と走行距離から求められる平均速度は調和平均の値である時速 48 km であって、算術平均によって求められる時速 50 km を平均とするのは適切ではない。もっとも、調和平均が適切な場合でもしばしば誤って算術平均が用いられる^[1]。

他の平均との関係

2数 a, b の3種のピタゴラス平均の幾何学的構成。H によって示されている紫色の線が調和平均を表す。A, G はそれぞれ算術平均、幾何平均を表す。また、Q は二乗平均平方根を表す。

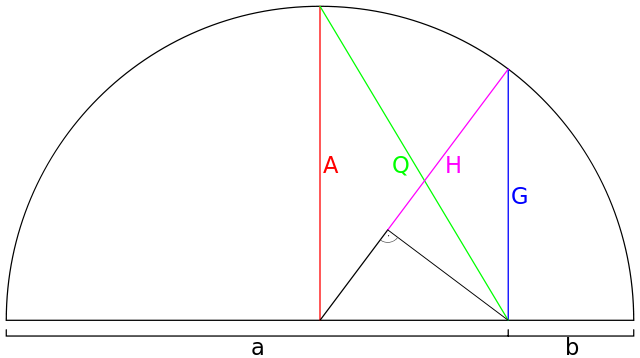
正の実数の集合に対して、調和平均を H, 算術平均を A, 幾何平均を G とすると、3つの平均の間には関係 H ≤ G ≤ A が成り立つ。平均を取る数の値がすべて等しいとき、かつそのときに限り、3つの平均は等しくなる。

また、2数 x₁, x₂ について考えると、調和平均は

${\displaystyle H={\frac {2x_{1}x_{2}}{x_{1}+x_{2}}}}$

と書ける。この場合算術平均は A = (x₁ + x₂)/2, 幾何平均は ${\displaystyle G={\sqrt {x_{1}x_{2}}}}$ であるから、

${\displaystyle H={\frac {G^{2}}{A}}}$

という関係が成り立つ。これは ${\displaystyle G={\sqrt {AH}}}$ とも書け、2つの数の幾何平均は算術平均と調和平均の幾何平均に等しいということである。

この関係は n（データ集合の大きさ）が3以上の場合に拡張することができ、一般の場合の関係は次のようになる：

${\displaystyle H(x_{1},\cdots ,x_{n})={\frac {(G(x_{1},\cdots ,x_{n}))^{n}}{A(x_{2}x_{3}\cdots x_{n},x_{1}x_{3}\cdots x_{n},\cdots ,x_{1}x_{2}\cdots x_{n-1})}}={\frac {(G(x_{1},\cdots ,x_{n}))^{n}}{A\left({\frac {\prod _{i=1}^{n}x_{i}}{x_{1}}},{\frac {\prod _{i=1}^{n}x_{i}}{x_{2}}},\cdots ,{\frac {\prod _{i=1}^{n}x_{i}}{x_{n}}}\right)}}.}$

この関係式は調和平均の定義式を変形した式

${\displaystyle H={\frac {n}{\sum \limits _{i=1}^{n}{\frac {1}{x_{i}}}}}={\frac {n\prod \limits _{j=1}^{n}x_{j}}{\sum \limits _{i=1}^{n}{\frac {\prod _{j=1}^{n}x_{j}}{x_{i}}}}}}$

から導かれる。

3つの数の平均では次の関係が成り立つ^[2]：

${\displaystyle {\frac {A^{3}}{G^{3}}}+{\frac {G^{3}}{H^{3}}}+1\leq {\frac {3}{4}}\left(1+{\frac {A}{H}}\right)^{2}}$

性質

• データに1つ以上の 0 があるとき、調和平均の定義式はそのままでは使えないが、 0 への極限を取ると、調和平均は 0 となる（x_i → 0 のとき H → 0）。また、データに負数があっても調和平均は計算することができる。ただし、正負が混在しているデータでは逆数の和が 0 になることがあり、この場合極限は発散する。
• 調和平均の値は、データ集合の中の最小の値に近付く傾向にある。このため、（算術平均に比べて）大きい外れ値の影響を和らげ小さい外れ値の影響を重くする傾向がある。
• あるデータ集合が異なるデータ集合を mean-preserving spread したものであれば（すなわち、データが算術平均を変えないまま分散が大きくなっていれば）調和平均はもとの集合のものより小さくなる^[3]。

例

物理学

物理学では、ある状況において、特に率や比を含む多くの状況において、調和平均は最も適切な平均を提供する。

例えば、乗り物がある距離を速度 x（例えば時速 60 km）で走りそれから同じ距離を速度 y（例えば時速 40 km）で走ると、平均速度は全距離を総走行時間を割ったものになるが、これは x と y の調和平均となる（時速 48 km）。調和平均が適切でない場合もあり、例としては、乗り物がある時間速度 x で走りそれから同じ時間速度 y で走る場合が考えられ、その平均速度は x と y の算術平均となる（同じ例では、時速 50 km）。3つ以上の異なる速度で走った場合でも同様となる。

異なる例として、2つの電気抵抗を接続することを考える。抵抗 x（例えば 60 Ω）と抵抗 y（例えば 40 Ω）とを並列に接続すると、その効果は x と y の調和平均 (48 Ω) に等しい同じ2つの抵抗を並列に接続した場合と同じである（合成抵抗の逆数が x の逆数と y の逆数との和に等しくなる）。また、この抵抗を直列に接続すると今度は x と y の算術平均 (50 Ω) に等しい抵抗を直列に接続したものと同じ効果となる（合成抵抗は x と y の和に等しい）。

このほかに調和平均を用いるのが適切な例としては、コンデンサを直列に接続する場合などが挙げられる。

なお、率や比を扱う場合でも重み付き平均を考えることが適切になることがあり、速度の例では複数の速度で異なる時間・異なる距離を走った場合が該当する。

数学

• 情報学分野においては、主に情報検索および機械学習に用いられるアルゴリズムやシステムを評価する際に、適合率と再現率の調和平均であるF値が用いられる。
• 代数学においては典型的な共同作業問題において調和平均が登場する。例えば、1つのプールから2本のパイプ A, B を用いて水を汲み出す問題が考えられる。このとき各々のパイプのみを用いた場合にはそれぞれ4時間、6時間を要するものとすると、2本のパイプを両方用いたときには (6 ⋅ 4)/(6 + 4), すなわち 2.4 時間を要するが、これは 6 と 4 の調和平均である 4.8 の半分である。
• 幾何学では調和平均が現れることがあり、以下のような例が挙げられる。
  • 任意の三角形において、内接円の半径は高さの調和平均の 1/3 である。
  • 正三角形 ABC の外接円の劣弧 BC 上の任意の点に対して、B と C からの距離をそれぞれ q と t として、PA と BC の交点が点 P から距離 y にあるとして、y は q と t の調和平均の 1/2 である^[4]。
  • 直角三角形において、脚を a, b, 直角に対する斜辺からの高さを h とすると、h² は a² と b² の調和平均の 1/2 である^[5][6]。
  • t と s (t > s) を斜辺 c の直角三角形の2つの内接四角形の辺とすると、s² は c² と t² の調和平均の 1/2 に等しい。
  • 台形の頂点を順に A, B, C, D として AB と CD が平行とする。E を対角線の交点とし、F を辺 DA 上にあるとし G を辺 BC 上にあるとし FEG は AB と CD に平行とする。すると FG は AB と DC の調和平均である。（これは相似な三角形を使って証明できる。）

  • 

    h は A と B の調和平均の 1/2 である。

    図のように、二つのはしごが通路の両端に立ててあり、高さ A および B の位置で脚とは反対側の壁に寄りかかっている場合を考える。このとき、はしごが交差する点の床からの高さ h は A と B の調和平均の 1/2 である。壁が斜めであっても、床からの各点の距離は壁との平行線を基準にすれば、A, B, h で変わらない。
  • 楕円において、semi-latus rectum（焦点から楕円への短軸に平行な直線に沿った距離）は焦点から楕円の最大と最小の距離の調和平均である。
• 三角関数において、タンジェントの二倍角の公式で、角 A について tan A = s/c と与えられていれば、tan 2A は、c, s の調和平均と、c − s の逆数の積である。数式で表現すれば

${\displaystyle \tan 2A={\frac {2cs}{c+s}}\cdot {\frac {1}{c-s}}}$

となる。例えば、

${\displaystyle \tan A={\frac {3}{7}}}$

であれば、最もよく知られた形の二倍角公式は

${\displaystyle \tan 2A={\frac {2\tan A}{1-\tan ^{2}A}}={\frac {2\cdot {\frac {3}{7}}}{1-({\frac {3}{7}})^{2}}}={\frac {21}{20}}}$

であるが、調和平均による公式を用いて

${\displaystyle \tan 2A={\frac {2\cdot 7\cdot 3}{7+3}}\cdot {\frac {1}{7-3}}={\frac {21}{20}}}$

とも書ける。

その他の例

• 水文学では、地層や土壌に対して平行な流れに対する透水係数の平均を考える際には算術平均を用いる一方、垂直な流れに対する透水係数の平均を考える際に調和平均が用いられる。この違いは、水文学における伝導性が抵抗性の逆数であることによって生じるものである。
• セイバーメトリクスでは選手の指標として、本塁打数と盗塁数の調和平均であるPower–speed numberが用いられる。
• 集団遺伝学においては、世代の個体数に急激な変動があった際の有効個体数（英語版）に及ぼす影響を計算するときに調和平均が用いられる。 これは、非常に個体数の少ない世代が実質的にボトルネックのようになることで、非常に少数の個体が遺伝子プールに不釣り合いに影響を及ぼし、結果として強い近親交配が起こりうることを考慮に入れるためである。
• 輸送においては速度を扱うため、物理学の場合と同様に調和平均や加重（重み付き）調和平均を用いる。
• 米国で自動車の燃費を表す際に主に使用される2つの単位 マイル毎ガロン および リットル毎 100 km の次元は互いに逆数の関係にある（前者は体積あたり距離で、後者は距離あたり体積）ので、広範な車の燃費の平均値を調べる際、一方の単位で算術平均を取ると、それは他方の単位の調和平均の関係になる。たとえば、リットル毎 100 km の単位で表された燃費の算術平均の値をマイル毎ガロンに変換すると、マイル毎ガロンの単位で表された燃費は調和平均の値になる。
• ファイナンス^{[要曖昧さ回避]}において調和平均は、株価収益率のような比率の平均を得るのに好ましい方法である。もしこれらの比率を算術平均すると（よくある間違い）、大きい値の方が小さい値よりも重みづけされる。一方で調和平均では、各値に等しい重みが与えられる^[7]。

脚注

[脚注の使い方]

1. Statistical Analysis, Ya-lun Chou, Holt International, 1969, ISBN 0030730953
2. Inequalities proposed in “Crux Mathematicorum”, . p. 74,#1834
3. Mitchell, Douglas W., "More on spreads and non-arithmetic means," The Mathematical Gazette 88, March 2004, 142-144.
4. Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, second edition, Dover Publ. Co., 1996, p.172.
5. Voles, Roger, "Integer solutions of a⁻² + b⁻² = d⁻²," Mathematical Gazette 83, July 1999, 269-271.
6. Richinick, Jennifer, "The upside-down Pythagorean Theorem," Mathematical Gazette 92, July 2008, 313-317.
7. "Fairness Opinions: Common Errors and Omissions", The Handbook of Business Valuation and Intellectual Property Analysis, McGraw Hill, 2004. ISBN 0071429670

関連項目

• 一般化平均（英語版）
• 重み付き平均（英語版）
• 調和数
• 割合

外部リンク

• 『調和平均』 - コトバンク
• 『調和平均にまつわる重要な公式まとめ』 - 高校数学の美しい物語
• Weisstein, Eric W. "Harmonic Mean". mathworld.wolfram.com (英語).
• Averages, Arithmetic and Harmonic Means at cut-the-knot