線型代数学 における計量ベクトル空間 （けいりょうベクトルくうかん、英 : metric vector space 内積 と呼ばれる付加的な構造 を備えたベクトル空間 であり、内積空間 （ないせきくうかん、英 : inner product space スカラー を対応付ける。内積によって、ベクトルの長さ や二つのベクトルの間の角度 などの直観的な幾何学的概念に対する厳密な導入が可能になる。また内積が零になることを以ってベクトルの間の直交性 に意味を持たせることもできる。内積空間は、内積として点乗積 （スカラー積）を備えたユークリッド空間 を任意の次元（無限次元でもよい）のベクトル空間に対して一般化するもので、特に無限次元のものは函数解析学 において研究される。
内積を用いたベクトルの成す角の定義の幾何学的解釈 内積はそれに付随するノルム を自然に導き、内積空間はノルム空間 の構造を持つ。内積に付随するノルムの定める距離に関して完備 となる空間はヒルベルト空間 と呼ばれ、必ずしも完備でない内積空間は（内積の導くノルムに関する完備化がヒルベルト空間となるから）前ヒルベルト空間 (pre-Hilbert space ) と呼ばれる。複素数体上の内積空間はしばしばユニタリ空間 (unitary spaces ) とも呼ばれる。
本項ではスカラー の体 F 実数 体 R 複素数 体 C
厳密に言えば、内積空間とは体 F ベクトル空間 V 内積 と呼ばれる写像
⟨
⋅
,
⋅
⟩
:
V
×
V
→
F
{\displaystyle \langle \cdot ,\cdot \rangle \colon V\times V\to F}
で以下の公理 を満足するものを備えたものを言う[1] [2]
共軛 対称性:
⟨
x
,
y
⟩
=
⟨
y
,
x
⟩
¯
.
{\displaystyle \langle x,y\rangle ={\overline {\langle y,x\rangle }}.}
第一引数に対する線型性:
⟨
a
x
+
y
,
z
⟩
=
a
⟨
x
,
z
⟩
+
⟨
y
,
z
⟩
.
{\displaystyle \langle ax+y,z\rangle =a\langle x,z\rangle +\langle y,z\rangle .}
正定値性 :
⟨
x
,
x
⟩
≥
0
,
[
⟨
x
,
x
⟩
=
0
⟹
x
=
0
]
{\displaystyle \langle x,x\rangle \geq 0,\quad [\langle x,x\rangle =0\implies x=0]}
F = R 対称性 に帰着される。
上記内積の定義において、係数体 を実数体 R C 順序体 を含む必要がある（従って、任意の順序体がそうであるように標数 が 0 でなければならない）ことである（ここから直ちに有限体は除外される）。また、係数体は区別された自己同型 (distinguished automorphism) のような付加構造を持たなければならない。そういう意味では、より一般に R C 代数的数 体）を考えれば十分だが、（R C 完備距離空間 にならない。これと対照的に、R C 完備 となり、従ってヒルベルト空間 になる。
計量ベクトル空間では様々な定理が成立する。
コーシー＝シュワルツの不等式 ：
⟨
x
,
y
⟩
2
≤
⟨
x
,
x
⟩
⋅
⟨
y
,
y
⟩
{\displaystyle \langle x,y\rangle ^{2}\leq \langle x,x\rangle \cdot \langle y,y\rangle }
様々なベクトル空間に様々な内積が定義できる。
最も単純な例として、実数 全体の成すベクトル空間に通常の乗法によって内積 ⟨ x , y ⟩ := xy
C n 正定値 エルミート行列 M
⟨
x
,
y
⟩
:=
y
†
M
x
=
x
†
M
y
¯
{\displaystyle \langle \mathbf {x} ,\mathbf {y} \rangle :=\mathbf {y} ^{\dagger }\mathbf {M} \mathbf {x} ={\overline {\mathbf {x} ^{\dagger }\mathbf {M} \mathbf {y} }}}
y † y 随伴行列 ）、エルミート形式 と呼ばれる。実係数の場合は、（正のスケール因子と拡大方向に直交する方向を持つ）二つのベクトルをそれぞれ異なる方向に拡大変換したものを点乗積することに相当する。これは直交変換の違いを除 けば、正の重みをもつ点乗積の重み付き和 （英語版 ） ヒルベルト空間 の項には、内積の導く距離が完備 となるような内積空間のさまざまな例がある。完備でないような内積を持つ内積空間には、例えば閉区間 [a , b ] C ([a , b ])
⟨
f
,
g
⟩
:=
∫
a
b
f
(
t
)
g
(
t
)
¯
d
t
{\displaystyle \langle f,g\rangle :=\int _{a}^{b}f(t){\overline {g(t)}}\,dt}
[−1, 1]
f
k
(
t
)
=
{
0
(
t
∈
[
−
1
,
0
]
)
1
(
t
∈
[
1
k
,
1
]
)
k
t
(
t
∈
(
0
,
1
k
)
{\displaystyle f_{k}(t)={\begin{cases}0&(t\in [-1,0])\\1&(t\in [{\tfrac {1}{k}},1])\\kt&(t\in (0,{\tfrac {1}{k}})\end{cases}}}
{fk }k を考えれば、この列は内積の導くノルムに関してコーシー列 を成すが、これは「連続」函数に収斂しないことを見ればよい。実確率変数 X , Y 期待値 ⟨ X , Y ⟩ := E (XY )⟨ X , X ⟩ = 0確率 に関して Pr(X = 0) = 1 X = 0殆ど確実 （英語版 ） 確率ベクトル （英語版 ）
実平方行列に対し、⟨ A , B ⟩ := tr(AB ⊤ )
⟨
A
,
B
⟩
¯
=
⟨
B
⊤
,
A
⊤
⟩
{\displaystyle {\overline {\langle A,B\rangle }}=\langle B^{\top },A^{\top }\rangle }
p ≠ 2
‖
x
‖
p
=
(
∑
i
=
1
∞
|
ξ
i
|
p
)
1
/
p
(
x
=
{
ξ
i
}
∈
ℓ
p
)
{\displaystyle \|x\|_{p}=\left(\sum _{i=1}^{\infty }|\xi _{i}|^{p}\right)^{1/p}\quad (x=\{\xi _{i}\}\in \ell ^{p})}
なるノルムをいれてノルム空間 を得ることはできるが、中線定理 （平行四辺形公式）を満たさないので内積空間にはならない（ノルムに付随する内積が存在するには中線定理が成り立たなければならない）[3] [4]
しかし内積空間ならば、内積から自然に定義され、中線定理を満足するノルム
‖
x
‖
=
⟨
x
,
x
⟩
{\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}}
を持つ。このノルムは内積の定義における正定値性公理によってきちんと定義される 。ノルムはベクトル x
コーシー＝シュワルツの不等式 V x , y
|
⟨
x
,
y
⟩
|
≤
‖
x
‖
⋅
‖
y
‖
{\displaystyle |\langle x,y\rangle |\leq \|x\|\cdot \|y\|}
x y 線型従属 であるとき、かつそのときに限り成立）。これは数学においてもっとも重要な不等式のうちの一つである。ロシア語の文献ではコーシー＝ブニャコフスキー＝シュワルツの不等式とも呼ぶ。重要性に鑑みて、簡潔な証明を記しておこう:
y = 0⟨ y , y ⟩
λ
=
⟨
y
,
y
⟩
−
1
⟨
x
,
y
⟩
{\displaystyle \lambda =\langle y,y\rangle ^{-1}\langle x,y\rangle }
0
≤
⟨
x
−
λ
y
,
x
−
λ
y
⟩
=
⟨
x
,
x
⟩
−
⟨
y
,
y
⟩
−
1
|
⟨
x
,
y
⟩
|
2
{\displaystyle 0\leq \langle x-\lambda y,x-\lambda y\rangle =\langle x,x\rangle -\langle y,y\rangle ^{-1}|\langle x,y\rangle |^{2}}
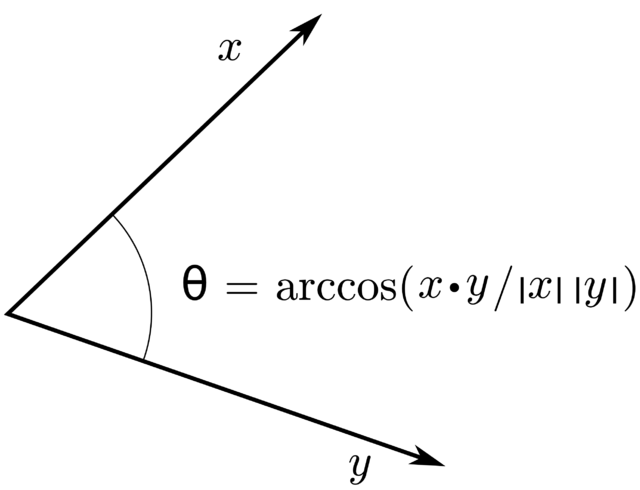
直交性 内積は角度や長さといった言葉で幾何学的に解釈することができるので、内積空間において幾何学的な用語法を用いる動機付けを与えるものとなる。実際、コーシー＝シュワルツの不等式の直接の帰結として、F = R x , y
angle
(
x
,
y
)
=
arccos
⟨
x
,
y
⟩
‖
x
‖
⋅
‖
y
‖
{\displaystyle \operatorname {angle} (x,y)=\arccos {\frac {\langle x,y\rangle }{\|x\|\cdot \|y\|}}}
[0, π] から選ぶものとする。これは二次元ユークリッド空間における場合の対応物になっている。F = C [0, π/2] は
angle
(
x
,
y
)
=
arccos
|
⟨
x
,
y
⟩
|
‖
x
‖
⋅
‖
y
‖
{\displaystyle \operatorname {angle} (x,y)=\arccos {\frac {|\langle x,y\rangle |}{\|x\|\cdot \|y\|}}}
V x , y 0 となることと定める。
斉次性 V x r ǁrx ǁ = |r | ǁx ǁ が成り立つ。三角不等式 V x , y ǁx + y ǁ ≤ ǁx ǁ + ǁy ǁ が成り立つ。斉次性と三角不等式は函数 ǁǁ が実際にノルムを成すことを示すものである。これにより V ノルム線型空間 となり、従ってまた距離空間 を成す。最も重要な内積空間は、この距離に関して完備距離空間 となるもので、それらはヒルベルト空間 と呼ばれる。任意の内積空間 V 稠密 な部分空間であり、このヒルベルト空間は V V
ピタゴラスの定理 V x , y ⟨x , y ⟩ = 0 を満たすならば ǁx ǁ2 + ǁy ǁ2 = ǁx + y ǁ2 が成り立つ。この等式の証明には、ノルムを定義に従って内積を用いて書いて、各成分に関する加法性に従って展開すれば十分である。「ピタゴラスの定理」という名称はこの結果を幾何学的に解釈したものが綜合幾何学 における同名の定理の類似対応物になっていることによる。無論、綜合幾何学におけるピタゴラスの定理の証明は、基礎に置かれた構造が乏しいために、より複雑なものとなることに注意すべきである。その意味において、綜合幾何学におけるピタゴラスの定理は、いま述べた内積空間におけるものよりも深い結果である。
ピタゴラスの定理に数学的帰納法 を適用することにより、x 1 , …, x n 直交系 、即ち相異なる任意の添字 j , k ⟨ x j x k ⟩ =0
∑
i
=
1
n
‖
x
i
‖
2
=
‖
∑
i
=
1
n
x
i
‖
2
{\displaystyle \sum _{i=1}^{n}\|x_{i}\|^{2}=\left\|\sum _{i=1}^{n}x_{i}\right\|^{2}}
となることが示せる。コーシー＝シュワルツの不等式から、⟨ ,⟩ : V × V → F 連続写像 となることも分かるから、ピタゴラスの定理を無限和にまで拡張することができる:
パーシヴァルの等式 V 完備 内積空間ならば、{x k } がどのに元も互いに直交する V
∑
i
=
1
∞
‖
x
i
‖
2
=
‖
∑
i
=
1
∞
x
i
‖
2
{\displaystyle \sum _{i=1}^{\infty }\|x_{i}\|^{2}=\left\|\sum _{i=1}^{\infty }x_{i}\right\|^{2}}
収斂 する限りにおいて成立する。空間の完備性は、部分和の列（これがコーシー列 となることは容易）が収斂することを保証するために必要である。
中線定理 V x , y ǁx + y ǁ2 + ǁx − y ǁ2 = 2ǁx ǁ2 + 2ǁy ǁ2 が成り立つ。実は中線定理はノルム空間において、そのノルムを導く内積が存在するための必要かつ十分な条件であり、これを満足するとき対応する内積は偏極恒等式
‖
x
+
y
‖
2
=
‖
x
‖
2
+
‖
y
‖
2
+
2
ℜ
⟨
x
,
y
⟩
{\displaystyle \|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}+2\Re \langle x,y\rangle }
によって与えられる（これは余弦定理 の一つの形である）。
V n 基底 はちょうど n グラム–シュミットの正規直交化法 を用いれば、任意の基底を正規直交基底に取り換えてから話を進めて良い。即ち、基底は各ベクトルが単位ノルムを持ち互いに直交するものとする。式で書けば、基底 {e 1 , …, e n } が正規直交であるとは、i ≠ j ⟨ e i e j ⟩ = 0i ⟨ e i e i ⟩ = ǁe i
この正規直交基底の定義は、以下のように無限次元内積空間に対して一般化することができる。V E = {e α ∈ V }α ∈ A V （位相的）基底 であるとは、E V V 稠密 となるときに言う。基底 E V α , β ∈ A α ≠ β ⟨ e α e β ⟩ = 0⟨ e α e α ⟩ = ǁe α
グラム-シュミットの方法の無限次元版を用いれば
定理 任意の可分 な内積空間 V が示される。また、ハウスドルフの極大原理 （英語版 ） 完備内積空間 において線型部分空間への直交射影が定義可能 であるという事実を用いれば、
定理 任意の完備内積空間 V も示せる。これら二つの定理は「任意の内積空間が正規直交基底を持ち得るか」という問いに答えるもので、これには否定的な結論が下される。これは非自明な結果であり、以下のような証明が知られている:
さらに見る
証明[5]
内積空間の次元とは、与えられた正規直交系を含む極大正規直交系の濃度であったことを思い出そう（ツォルンの補題により、そのような極大系は少なくとも一つ存在し、またそのような極大系はどの二つも同じ濃度を持つのであった）。一つの正規直交基底は極大正規直交系であるが、逆は必ずしも成り立たないことは既知である。G H G H H G H K ℵ 0 K = ℓ2 (N )E K |E | = ℵ 0 である。基底 E K ハメル基底（代数基底） E ∪ F E ∩ F = ∅ K 連続体濃度 c |F | = c でなければならない。
L c L = ℓ2 (R )L B φ : F → B T : K → L Tf = φ (f )f ∈ F Te = 0e ∈ E
H = K ⊕ L G = {(k , Tk ) : k ∈ K T G G H G H e ∈ E (e , 0) ∈ G ゆえ、K ⊕ 0 ⊂ G
次に、b ∈ B f ∈ F ⊂ K b = Tf (f , b ) ∈ G ⊂ G である。同様に (f , 0) ∈ G ゆえ、(0,b ) ∈ G もわかる。従って 0 ⊕ L ⊂ G であり、G H G H
最後に {(e ,0) : e ∈ E } が G
0
=
⟨
(
e
,
0
)
,
(
k
,
T
k
)
⟩
=
⟨
e
,
k
⟩
+
⟨
0
,
T
k
⟩
=
⟨
e
,
k
⟩
{\displaystyle 0=\langle (e,0),(k,Tk)\rangle =\langle e,k\rangle +\langle 0,Tk\rangle =\langle e,k\rangle }
が任意の e ∈ E k = 0(k , Tk ) = (0,0) は G G |E | = ℵ 0 となるが、一方 H c
閉じる
パーシヴァルの等式 から直ちに次が従う。
定理 可分内積空間 V e k k
x
↦
{
⟨
e
k
,
x
⟩
}
k
∈
N
{\displaystyle x\mapsto \{\langle e_{k},x\rangle \}_{k\in \mathbb {N} }}
V → ℓ 2 この定理はフーリエ級数 の抽象版であり、任意の正規直交基底がフーリエ級数における三角多項式 の成す直交系の役割を果たす。上記の添字集合は任意の可算集合としてよい（また実は、ヒルベルト空間 の項にあるように、そうして得られる空間は全て、適当な集合上で定義された ℓ 2
定理 V C[− π ,π ] ならば、整数全体の成す集合で添字付けられた連続函数の双無限列
e
k
(
t
)
=
e
i
k
t
2
π
{\displaystyle e_{k}(t)={\frac {e^{ikt}}{\sqrt {2\pi }}}}
L 2 C[− π ,π ] の正規直交基底であり、写像
f
↦
{
1
2
π
∫
−
π
π
f
(
t
)
e
−
i
k
t
d
t
}
k
∈
Z
{\displaystyle f\mapsto \left\{{\frac {1}{\sqrt {2\pi }}}\int _{-\pi }^{\pi }f(t)e^{-ikt}\,dt\right\}_{k\in \mathbb {Z} }}
点列 {ek }k k ≠ j
∫
−
π
π
e
−
i
(
j
−
k
)
t
d
t
=
0
{\displaystyle \int _{-\pi }^{\pi }e^{-i(j-k)t}\,dt=0}
から直ちにわかる。正規性は列の作り方による（即ち、列の各係数はノルムが 1 となるように選ばれたものである）。
最後に、この列が内積の定めるノルムに関して稠密な（代数的）線型包 を持つことは、このとき [− π ,π ] 上の連続な周期函数が一様ノルムに関して成すノルム空間においてこの列が稠密な線型包を持つことから従う。これは、三角多項式の一様稠密性に関するヴァイエルシュトラスの定理の内容である。
内積空間 V W A : V → W
連続線型写像 A x V {ǁAx ǁ } が有界。対称線型作用素: V x , y ⟨ Ax , y ⟩ = ⟨ x , Ay ⟩
等長作用素 V x , y ⟨ Ax , Ay ⟩ = ⟨ x , y ⟩ V x ǁAx ǁ = ǁx ǁ が成り立つ。任意の等長作用素は単射 であり、また等長作用素は内積空間の間の準同型 、特に実内積空間の間の準同型は直交作用素 である（直交行列 と比較せよ）。等長同型 : A 全射 （従って全単射 ）。等長同型はユニタリ作用素とも呼ばれる（ユニタリ行列 と比較せよ）。内積空間論の観点からは、互いに等長同型な二つの空間は区別を要しない。スペクトル定理 は有限次元内積空間上の対称作用素、ユニタリ作用素、あるいは一般に正規作用素 に対する標準形を与えるものである。スペクトル定理の一般化はヒルベルト空間上の連続正規作用素に対しても成り立つ。
Halmos, P.R (1982). A Hilbert Space Problem Book . Graduate Texts in Mathematics. Springer. ISBN 978-0387906850 
...
![{\displaystyle \langle x,x\rangle \geq 0,\quad [\langle x,x\rangle =0\implies x=0]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3ded98456caa1fe8b5e0040f201d9ac375b1dee6)
![{\displaystyle f_{k}(t)={\begin{cases}0&(t\in [-1,0])\\1&(t\in [{\tfrac {1}{k}},1])\\kt&(t\in (0,{\tfrac {1}{k}})\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b62b2e6556a15f3f2e47a1e077441a17d6ecd64c)
