Geometria sferica

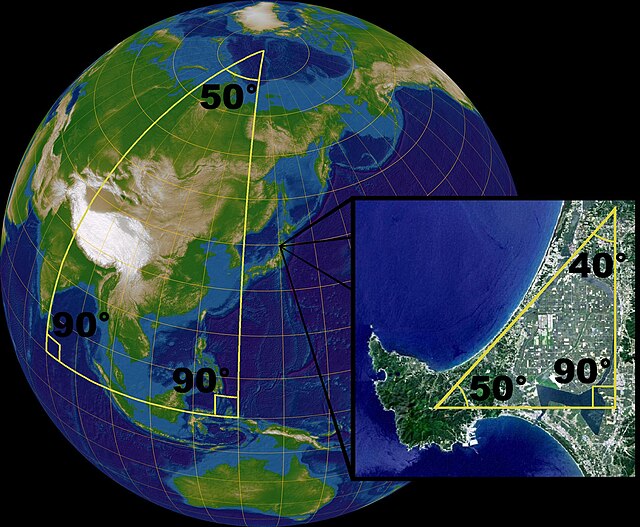
La geometria sferica è una geometria non euclidea ideata dal matematico Bernhard Riemann. La geometria sferica possiede una immediata interpretazione nella geometria euclidea. Infatti il suo modello si presenta come "descritto" dalla geometria della superficie di una sfera. Ha applicazioni pratiche nella navigazione e nell'astronomia.

Su una sfera, la somma degli angoli interni di un triangolo non è uguale a 180°. La sfera non è uno spazio euclideo, ma localmente le leggi della geometria euclidea forniscono buone approssimazioni.

La geometria sferica nasce dalla negazione del V postulato di Euclide, o equivalentemente dal IV.1 postulato di Hilbert. Tuttavia, affinché sia una teoria assiomatica coerente, è necessario modificare anche gli assiomi di incidenza e di ordinamento della geometria euclidea (nel caso della geometria ellittica solo quello di ordinamento)^[1]. Essa è caratterizzata dall'assenza di rette parallele.

Di seguito presentiamo prima il corpo assiomatico della geometria sferica piana e successivamente ne analizzeremo un suo modello. Per una comprensione più intuitiva si può, volendo, leggere prima della trattazione assiomatica il seguente paragrafo: Modello di geometria sferica.

Corpo assiomatico

Con riferimento alla classificazione assiomatica proposta da Hilbert per la geometria euclidea, riportiamo di seguito quella relativa alla geometria sferica piana.

I concetti primitivi sono il punto, le coppie di punti detti punti antipodali, la retta, e il piano. Ci sono anche due relazioni binarie ed una relazione quaternaria primitive:

• Contiene: un punto può essere contenuto in una retta o in un piano, ed una retta può essere contenuta in un piano;
• Separa: la coppia di punti AB separa la coppia di punti CD, in simboli: S(AB|CD) (relazione quaternaria);
• Congruenza, indicata con il simbolo "≡": angoli e segmenti possono essere congruenti.

Il segmento fra due punti A e B è definito come la porzione di retta compresa tra i punti A e B (inclusi A e B).

I - Assiomi di appartenenza

1. L'insieme dei punti del piano è suddiviso in coppie di punti, tali che ogni punto del piano appartiene ad una e una sola coppia e i punti di ciascuna coppia sono distinti. Per due punti che appartengono a coppie distinte, passa una ed una sola retta mentre per i due punti di una stessa coppia passano più rette.
2. Su ogni retta vi sono almeno tre punti.
3. Non tutti i punti appartengono alla stessa retta.

II - Assiomi di ordinamento

1. Se S (AB | CD), allora A, B, C, D sono quattro punti distinti appartenenti alla stessa retta.
2. Se S (AB | CD), allora: S (BA | CD); S (AB | DC); S (BA | DC); S (CD | AB); S (CD | BA); S (DC | AB); S (DC | BA).
3. Se A, B, C sono tre punti di una retta, allora esiste almeno un punto D tale che S (AB | CD).
4. Se A, B, C, D sono quattro punti distinti appartenenti alla stessa retta, allora esiste una coppia di punti che separa la coppia costituita dagli altri due; vale cioè almeno una delle seguenti relazioni: S (AB | CD), S (AC | BD), S (AD | BC).
5. Se S (AB | CD) e S (AC | BE), allora S (AB | DE).
6. Una retta che, passante per un vertice, entra in un triangolo, incontra il lato opposto.

III - Assiomi di congruenza

1. Se A, B sono due punti di una retta ed inoltre A' è un punto sulla stessa retta ovvero su un'altra a', si può sempre trovare un punto B', da una data parte della retta a' rispetto ad A', tale che il segmento AB sia congruente, ovvero uguale, al segmento A'B' ; in simboli: AB ≡ A'B' .
2. Se un segmento A'B' ed un segmento A”B” sono congruenti ad uno stesso segmento AB, A'B' ≡ AB e A”B” ≡ AB , allora anche il segmento A'B' è congruente al segmento A”B”.
3. Siano AB e BC due segmenti senza punti in comune (questo vuol dire che i punti A e C sono opposti rispetto a B) su una retta a ed A'B' e B'C' due segmenti sulla stessa retta o su un'altra a', sempre senza punti in comune. Allora se è AB ≡ A'B' e BC ≡ B'C' , è pure AC ≡ A'C'.
4. Siano dati un angolo α(h,k) in un piano α ed una retta a' in un piano α', come pure un determinato lato di a' in α'. Si indichi con h' una semiretta della retta a' che abbia origine in O'. C'è allora nel piano una ed una sola semiretta k' tale che l'angolo α(h,k) è congruente, ovvero uguale, all'angolo α(h',k') ed allo stesso tempo tutti i punti interni all'angolo α(h',k') che stanno dalla parte di a'.
5. Se per due triangoli ABC ed A'B'C' valgono le congruenze AB ≡ A'B', AC ≡ A'C', αABC ≡ αA'B'C', Allora è sempre valida la congruenza: αABC ≡ αA'B'C'.

IV - Assioma di Riemann

1. Due rette qualsiasi di un piano hanno sempre almeno un punto in comune.

V - Assioma di continuità (o di Dedekind)

1. Se i punti di un segmento AB sono divisi in due classi non vuote in modo che:
   a) tutti i punti di AB siano in una o nell'altra classe (e in una sola);
   b) i punti A e B appartengono a classi diverse (che chiameremo rispettivamente I e II classe);
   c) tutti i punti della I classe precedono quelli della II;
   allora esiste nel segmento AB un punto C (che può appartenere sia alla I che alla II classe) tale che tutti i punti del segmento AB che precedono C appartengono alla I classe, e tutti quelli che seguono C appartengono alla II classe. C si dice punto di separazione tra le due classi.

Modello di geometria sferica

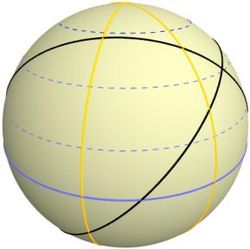
Come già accennato precedentemente un modello di geometria sferica è quello costruito su una sfera come preciseremo di seguito. Nella geometria piana i concetti base sono il punto e la retta. Su una sfera, i punti sono definiti nel senso usuale. Le rette sono definite come cerchi massimi. Pertanto, nella geometria sferica gli angoli sono definiti tra cerchi massimi, e ne deriva una trigonometria nel piano sferico che differisce dalla trigonometria euclidea nel piano (ad esempio, la somma degli angoli interni di un triangolo è maggiore di un angolo piatto). Invece la trigonometria sferica nello spazio sferico (ma anche in quello ellittico), se si adottano opportune convenzioni sulla misura dei lati e degli angoli dei triangoli sferici, coincide con la trigonometria sferica euclidea ed iperbolica. Cioè la trigonometria sferica appartiene al corpo della geometria assoluta.
La distanza tra due punti della sfera è il segmento minimo che li unisce, geodetica.

Numero di triangoli che si formano dall'intersezione di tre rette.

Uno degli angoli individuato da due rette incidenti.

piano	insieme dei punti di una superficie sferica dello spazio euclideo
punto	punto della superficie della sfera
retta	circonferenza massima della superficie sferica (circonferenza di intersezione della superficie sferica con un piano passante per il centro della sfera)
segmento	parte di una retta delimitato da due punti della retta stessa
appartenenza	usuale appartenenza in senso euclideo
punti antipodali	punti diametralmente opposti della superficie sferica
congruenza tra segmenti	congruenza tra archi di circonferenza massima in geometria euclidea (definita mediante la congruenza delle corde o mediante i movimenti della sfera)
angolo tra due rette	angolo diedro tra i due piani che tagliano la sfera secondo le due rette, oppure angolo che coincide con l'angolo delle due rette euclidee tangenti alla sfera nel punto di intersezione delle due rette sferiche e giacenti nei piani da esse individuati
congruenza tra angoli	congruenza tra angoli in senso euclideo

In base a tale interpretazione (modello) tutti gli assiomi e le proprietà della geometria sferica risultano essere proposizioni in geometria euclidea. infatti, ad esempio, per due punti antipodali passano infinite rette.

Le rette sono i cerchi massimi (linee continue viola, nere, gialle). In figura le circonferenze tratteggiate in grigio non sono né rette né segmenti, ma curve.

Cubo sferico.

Teoremi

• La circonferenza
  La circonferenza è definita come il luogo dei punti equidistanti da un punto dato detto centro. Si dimostra che una circonferenza può anche essere definita come il luogo dei punti equidistanti da una retta data.
• Area di un Triangolo
  Dato un triangolo sferico costruito su una sfera di raggio R di angoli ${\displaystyle \alpha ,\beta ,\gamma }$, l'area A del triangolo è:
  ${\displaystyle A=R^{2}(\alpha +\beta +\gamma -\pi )}$^[2].
• Somma degli angoli interni di un triangolo
  Dalla relazione precedente subito discende che la somma degli angoli interni di un triangolo è sempre maggiore di ${\displaystyle \pi }$ e minore di 3${\displaystyle \pi }$:
  ${\displaystyle \alpha +\beta +\gamma =\pi +A/R^{2}}$.
• Criteri di congruenza tra triangoli
  Sono uguali due triangoli sferici che abbiano ordinatamente uguali:

1. due lati e l'angolo compreso;
2. due angoli e il lato comune
3. i tre lati;
4. i tre angoli.

• Teorema di Pitagora
  Se ABC è un triangolo sferico retto in A e con ipotenusa a, e con b e c le lunghezze dei suoi lati, allora il coseno dell'ipotenusa è uguale al prodotto dei coseni dei cateti: ${\displaystyle \cos(a/k)=\cos(b/k)\cos(c/k)}$^[3] Facendo lo sviluppo in serie al secondo ordine delle funzioni trigonometriche, si ottiene l'espressione universalmente nota del Teorema di Pitagora in geometria euclidea: ${\displaystyle a^{2}=b^{2}+c^{2}}$
• Area di un poligono sferico
  L'area di un poligono sferico di n lati è:
  ${\displaystyle A=R^{2}(\alpha _{1}+\alpha _{2}+...+\alpha _{n}-(n-2)\pi )}$.
  La sua dimostrazione si basa sulla possibilità di scomporre un poligono sferico in triangoli.
• Formula di eulero
  Dato un poliedro sferico convesso con V vertici, S spigoli ed F facce, vale:
  V-S+F=2.
• Tutte le perpendicolari ad una retta concorrono in due punti, punti antipodali.
• Due punti antipodali dividono la retta in due parti congruenti.
• Due punti antipodali dividono in due parti congruenti tutte le rette che passano per essi.
• Tutte le rette sono congruenti.
• Dati quattro punti distinti A, B, C, D di una stessa retta, vale al più una delle seguenti relazioni: S(AB|CD), S(AC|BD), S(AD|BC).
• In un triangolo rettangolo l'angolo opposto ad uno dei due lati dell'angolo retto è acuto, ottuso o retto a seconda che tale lato è minore, maggiore o congruente all'altro lato dell'angolo retto.

Triangolo sferico

Varietà sferiche

Oltre alla sfera bidimensionale, altri spazi hanno una geometria sferica: questi spazi vengono denominati varietà sferiche. La geometria sferica è data formalmente da una struttura di varietà riemanniana con curvatura sezionale ovunque pari a 1.

I modelli base di varietà sferiche sono le sfere ${\displaystyle S^{n}}$ di dimensione arbitraria (ad esempio la sfera tridimensionale ${\displaystyle S^{3}}$). Tutte le altre varietà sferiche hanno la struttura locale di una sfera, ma possono avere una diversa topologia globale: tra questi ci sono gli spazi proiettivi, ottenuti identificando i punti antipodali di una sfera, che non sono orientabili in dimensione ${\displaystyle n}$ pari. In dimensione ${\displaystyle n=3}$ ci sono anche gli spazi lenticolari.

Note

1. Per saperne di più sulla genesi della geometria sferica si veda qui
2. ${\displaystyle (\alpha +\beta +\gamma -\pi )}$ è detto eccesso angolare.
3. k è un parametro dimensionale che dipende dalle unità di misura scelto per indicare le misure dei lati del triangolo.

Bibliografia

• Le Geometrie non Euclidee e i fondamenti della geometria di E. Agazzi, D. Palladino – Edizioni Scientifiche e Tecniche Mondadori.

Voci correlate

• Trigonometria sferica
• Eversione della sfera
• Geometria euclidea
• Geometria non euclidea
• V postulato di Euclide
• Assiomi di Hilbert
• Geometria ellittica
• Geometria iperbolica
• Geometria proiettiva

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su geometria sferica

Collegamenti esterni

• (EN) spherical geometry, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Geometria sferica, su MathWorld, Wolfram Research.
• (en) La geometria sulla sfera
• La geometria sulla sfera, su users.libero.it.
• Geometrie non euclidee, su progettomatematica.dm.unibo.it.

Controllo di autorità	Thesaurus BNCF 71579 · GND (DE) 4182228-6 · NDL (EN, JA) 01212460

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica