Teoria della coalescenza

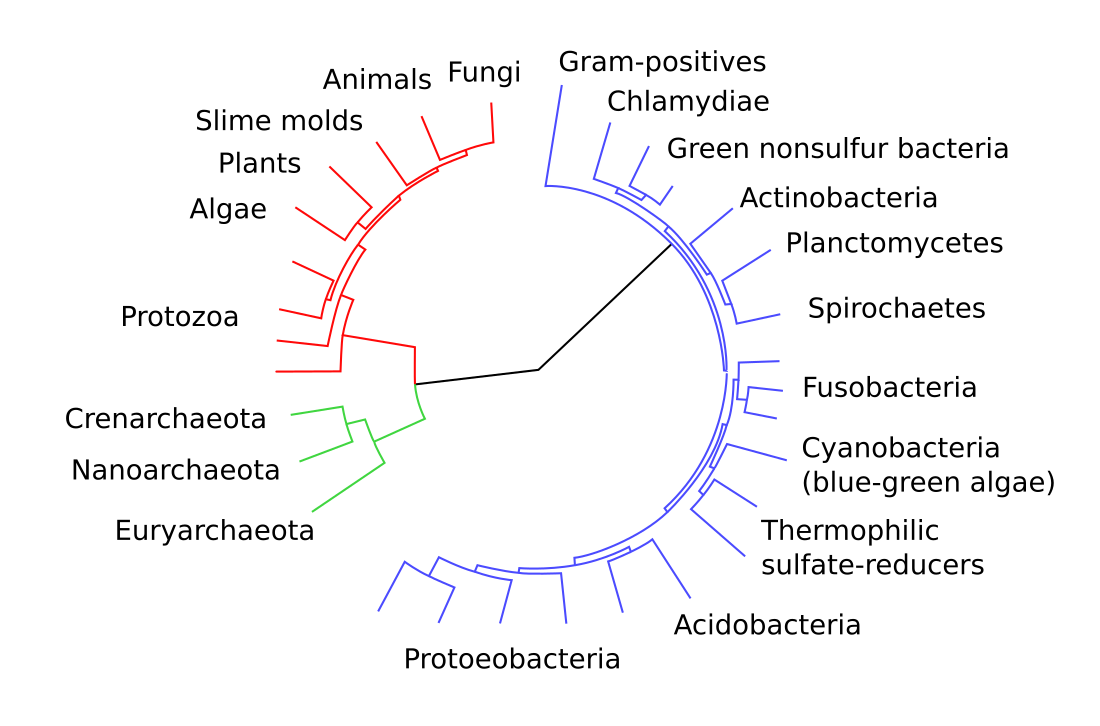
In genetica, la teoria coalescente è un modello matematico della genetica delle popolazioni. Originariamente sviluppato nei primi anni ottanta da John Kingman^[1], viene impiegato nel tentativo di rintracciare tutti gli alleli di un gene comune a tutti i membri di una popolazione derivanti da un unico esemplare ancestrale, conosciuto come il più recente antenato comune (MRCA - Most Recent Common Ancestor), a volte denominato anche il coancestor, per sottolineare il rapporto coalescente^[2]. Le relazioni di ereditarietà tra gli alleli sono in genere rappresentate come una genealogia genetica, simile nella forma a un albero filogenetico. Questa genealogia genica è nota anche come coalescenza.

I modelli coalescenti vengono costruiti a ritroso, basandosi sulle mappe e sugli alberi filogenetici. La teoria coalescente semplificata non contempla i casi di ricombinazione, azione della selezione naturale, esclude il flusso genico ed i cambiamenti strutturali della popolazione, mentre i modelli statistici più complessi consentono ai ricercatori di includere nelle indagini di coalescenza anche i casi di ricombinazione, selezione, e praticamente qualsiasi modello evolutivo o demografico presente all'interno dell'analisi genetica delle popolazioni.

Principio di coalescenza

Dati due organismi appartenenti a due linee (rette) distinte aploidi che differiscono in un singolo nucleotide, tracciando l'ascendenza di questi due individui (andando a ritroso nel tempo) ci sarà un momento in cui le due linee convergono; il punto di incontro delle rette è l'MRCA.

Storia

La Teoria della coalescenza è un'estensione del concetto di popolazione genetica dell'evoluzione neutrale ed è un'approssimazione del modello Fisher-Wright (o di Wright-Fisher) modello per popolazioni di grandi dimensioni. Nel corso degli anni '80 del XX secolo, diversi autori indipendentemente l'uno dall'altro, svilupparono questo modello, ma la formalizzazione definitiva viene attribuita a Kingman^[3][4][5][6].

Contributi importanti allo sviluppo della teoria coalescente sono stati forniti da Peter Donnelly, Robert Griffiths, Richard Hudson R e Simon Tavare. Ciò ha comportato variazioni incorporando la possibilità di aumenti nella dimensione della popolazione, nel calcolo di ricombinazione e selezione. Nel 1999 Jim Pitman e Serik Sagitov, indipendentemente, introdussero processi coalescenti con collisioni multiple di lignaggi ancestrali. Agli studi di Martin Möhle, Serik Sagitov e Jason Schweinsberg si deve la scoperta della possibilità di fusioni multiple simultanee di lignaggi ancestrali^[7][8].

Calcolo della variabile tempo

Un'analisi utile basata sulla teoria coalescente è un'analisi matematica mirata a prevedere la quantità di tempo trascorso tra l'introduzione di una mutazione e la risultante di un particolare allele o distribuzione genetica in una popolazione. Questo periodo di tempo è uguale al tempo di comparsa del più recente antenato comune.

La probabilità che due linee si fondano nella generazione immediatamente precedente è proporzionale alla probabilità che le stesse condividano un genitore comune.

In una popolazione diploide, con una effettiva dimensione costante della popolazione N_e, le copie di ogni locus, considerando che ci sono 2 "potenziali genitori" nella generazione precedente, saranno pari a 2N_e. Qualsiasi caratteristica di una popolazione reale che si scosta da quelle di una popolazione ideale determinerà una differenza tra dimensione effettiva costante N_e e dimensione censita reale N_c. In generale le popolazioni reali non seguono le assunzioni definite per quelle ideali per cui spesso si osservano delle deviazioni che portano a^[9]:

${\displaystyle {2N_{e}}<{2N_{c}}}$

La probabilità che i due alleli hanno di condividere un genitore è uguale a 1/(2N_e) e di conseguenza, la probabilità di non coalescenza sarà invece pari a 1-1/(2N_e).

Ad ogni successiva generazione precedente, la probabilità di coalescenza è distribuita geometricamente - cioè, è data dalla probabilità di noncoalescenze al t-1 di generazioni precedenti, moltiplicata per la probabilità di coalescenza alla generazione di interesse:

${\displaystyle P_{c}(t)=\left(1-{\frac {1}{2N_{e}}}\right)^{t-1}\left({\frac {1}{2N_{e}}}\right).}$

Per valori sufficientemente grandi di N_e, questa distribuzione è ben approssimata dalla distribuzione continua esponenziale:

${\displaystyle P_{c}(t)={\frac {1}{2N_{e}}}e^{-{\frac {t-1}{2N_{e}}}}.}$

La distribuzione standard esponenziale ha sia il valore atteso che la deviazione standard pari a 2N_e, quindi, anche se il tempo previsto per coalescenza è 2N_e, i tempi di coalescenza reali hanno una vasta gamma di variazione. Si noti che il tempo di coalescenza è il numero di generazioni precedenti dove la coalescenza ha avuto luogo.

Per ricavare il tempo cronologico è possibile eseguire una stima moltiplicando il valore di 2N_e con il tempo medio tra le generazioni dell'organismo indagato.

Calcolo dell'eterozigosi media

L'eterozigosi media, rappresentata con il simbolo ${\displaystyle {\bar {H}}}$, è la quantità di variazione genomica attesa dall'azione della deriva genetica.

L'eterozigosi media viene calcolata come la probabilità di una mutazione, in una determinata generazione, divisa per la probabilità di ogni "evento" in quella generazione. La probabilità che l'evento sia una mutazione è la probabilità di una mutazione in una delle due linee: ${\displaystyle 2\mu }$. Così l'eterozigosi media è uguale a:

${\displaystyle {\bar {H}}={\frac {2\mu }{2\mu +{\frac {1}{2N_{e}}}}};}$

${\displaystyle {\bar {H}}={\frac {4N_{e}\mu }{1+4N_{e}\mu }};}$

${\displaystyle {\bar {H}}={\frac {\theta }{1+\theta }}.}$

Per ${\displaystyle 4N_{e}\mu \gg 1}$ la grande maggioranza delle coppie di alleli hanno almeno una differenza nella sequenza nucleotidica.

Software e simulatori

• TreesimJ ^{[collegamento interrotto]}, su staff.washington.edu.
• BEAST, su beast.bio.ed.ac.uk.
• CoaSim, su daimi.au.dk. URL consultato il 21 marzo 2012 (archiviato dall'url originale il 5 febbraio 2012).
• GeneRecon, su daimi.au.dk. URL consultato il 21 marzo 2012 (archiviato dall'url originale il 5 febbraio 2012).
• genetree, su stats.ox.ac.uk. URL consultato il 21 marzo 2012 (archiviato dall'url originale il 5 febbraio 2012).

Note

1. Rousset F. and Leblois R. (2007) Likelihood and Approximate Likelihood Analyses of Genetic Structure in a Linear Habitat: Performance and Robustness to Model Mis-Specification Molecular Biology and Evolution 24:2730–2745
2. Harding, Rosalind, M. 1998. New phylogenies: an introductory look at the coalescent. pp. 15–22, in Harvey, P. H., Brown, A. J. L., Smith, J. M., Nee, S. New uses for new phylogenies. Oxford University Press (ISBN 0198549849)
3. Kingman, J.F.C. (1982) On the Genealogy of Large Populations. Journal of Applied Probability 19A:27–43 JSTOR copy
4. Hudson RR (1983a) Testing the constant-rate neutral allele model with protein sequence data. Evolution 37: 203–207 JSTOR copy
5. Hudson RR (1983b) Properties of a neutral allele model with intragenic recombination. Theoretical Population Biology 23:183–201.
6. Tajima, F. (1983) Evolutionary Relationship of DNA Sequences in finite populations. Genetics 105:437–460
7. Möhle, M., Sagitov, S. (2001) A classification of coalescent processes for haploid exchangeable population models The Annals of Probability 29:1547–1562
8. Schweinsberg, J. (2000) Coalescents with simultaneous multiple collisions Electronic Journal of Probability 5:1–50
9. Riccioni Giulia (2008) Cambiamenti temporali nella genetica del tonno rosso (Thunnus thynnus) del Mediterraneo; Università degli studi di Ferrara: DOTTORATO DI RICERCA IN BIOLOGIA EVOLUZIONISTICA E AMBIENTALE http://eprints.unife.it/145/1/Riccioni_Giulia09.pdf Archiviato il 17 aprile 2012 in Internet Archive.

Bibliografia

Articoli

• Arenas, M. and Posada, D. (2007) Recodon: Coalescent simulation of coding DNA sequences with recombination, migration and demography. BMC Bioinformatics 8: 458
• Arenas, M. and Posada, D. (2010) Coalescent simulation of intracodon recombination. Genetics 184(2): 429–437
• Browning, S.R. (2006) Multilocus association mapping using variable-length markov chains. American Journal of Human Genetics 78:903–913
• Degnan, JH and LA Salter. 2005. Gene tree distributions under the coalescent process. Evolution 59(1): 24-37. pdf from coaltree.net/
• Donnelly, P., Tavaré, S. (1995) Coalescents and genealogical structure under neutrality. Annual Review of Genetics 29:401–421
• Hellenthal, G., Stephens M. (2006) msHOT: modifying Hudson's ms simulator to incorporate crossover and gene conversion hotspots Bioinformatics AOP
• Hudson RR (1983a) Testing the constant-rate neutral allele model with protein sequence data. Evolution 37: 203–207 JSTOR copy^{[collegamento interrotto]}
• Hudson RR (1983b) Properties of a neutral allele model with intragenic recombination. Theoretical Population Biology 23:183–201.
• Hudson RR (1991) Gene genealogies and the coalescent process. Oxford Surveys in Evolutionary Biology 7: 1–44
• Hudson RR (2002) Generating samples under a Wright–Fisher neutral model. Bioinformatics 18:337–338
• Hein, J. , Schierup, M., Wiuf C. (2004) Gene Genealogies, Variation and Evolution: A Primer in Coalescent Theory Oxford University Press ISBN 978-0198529965
• Kaplan, N.L., Darden, T., Hudson, R.R. (1988) The coalescent process in models with selection. Genetics 120:819–829
• Kingman, J.F.C. (1982) On the Genealogy of Large Populations. Journal of Applied Probability 19A:27–43 JSTOR copy^{[collegamento interrotto]}
• Kingman, J.F.C. (2000) Origins of the coalescent 1974–1982. Genetics 156:1461–1463
• Liang L., Zöllner S., Abecasis G.R. (2007) GENOME: a rapid coalescent-based whole genome simulator. Bioinformatics 23: 1565–1567
• Mailund, T., Schierup, M.H., Pedersen, C.N.S., Mechlenborg, P.J.M., Madsen, J.N., Schauser, L. (2005) CoaSim: A Flexible Environment for Simulating Genetic Data under Coalescent Models BMC Bioinformatics 6:252
• Möhle, M., Sagitov, S. (2001) A classification of coalescent processes for haploid exchangeable population models The Annals of Probability 29:1547–1562
• Morris, A. P., Whittaker, J. C., Balding, D. J. (2002) Fine-scale mapping of disease loci via shattered coalescent modeling of genealogies American Journal of Human Genetics 70:686–707
• Neuhauser, C., Krone, S.M. (1997) The genealogy of samples in models with selection Genetics 145 519–534
• Pitman, J. (1999) Coalescents with multiple collisions The Annals of Probability 27:1870–1902
• Harding, Rosalind, M. 1998. New phylogenies: an introductory look at the coalescent. pp. 15–22, in Harvey, P. H., Brown, A. J. L., Smith, J. M., Nee, S. New uses for new phylogenies. Oxford University Press (ISBN 0198549849)
• Rosenberg, N.A., Nordborg, M. (2002) Genealogical Trees, Coalescent Theory and the Analysis of Genetic Polymorphisms. Nature Reviews Genetics 3:380–390
• Sagitov, S. (1999) The general coalescent with asynchronous mergers of ancestral lines Journal of Applied Probability 36:1116–1125
• Schweinsberg, J. (2000) Coalescents with simultaneous multiple collisions Electronic Journal of Probability 5:1–50
• Slatkin, M. (2001) Simulating genealogies of selected alleles in populations of variable size Genetic Research 145:519–534
• Tajima, F. (1983) Evolutionary Relationship of DNA Sequences in finite populations. Genetics 105:437–460
• Zöllner S. and Pritchard J.K. (2005) Coalescent-Based Association Mapping and Fine Mapping of Complex Trait Loci Genetics 169:1071–1092
• Rousset F. and Leblois R. (2007) Likelihood and Approximate Likelihood Analyses of Genetic Structure in a Linear Habitat: Performance and Robustness to Model Mis-Specification Molecular Biology and Evolution 24:2730–2745
• Leblois R., Estoup A. and Rousset F. (2009) IBDSim: a computer program to simulate genotypic data under isolation by distance Molecular Ecology Resources 9:107-109

Libri

• Hein, J; Schierup, M. H., and Wiuf, C. Gene Genealogies, Variation and Evolution – A Primer in Coalescent Theory. Oxford University Press, 2005. ISBN 0-19-852996-1.
• Nordborg, M. (2001) Introduction to Coalescent Theory
• Chapter 7 in Balding, D., Bishop, M., Cannings, C., editors, Handbook of Statistical Genetics. Wiley ISBN 978-0471860945
• Wakeley J. (2006) An Introduction to Coalescent Theory Roberts & Co ISBN 0-9747077-5-9 Accompanying website with sample chapters
• Rice SH. (2004). Evolutionary Theory: Mathematical and Conceptual Foundations. Sinauer Associates: Sunderland, MA. See esp. ch. 3 for detailed derivations.
• Berestycki N. "Recent progress in coalescent theory" 2009 ENSAIOS Matematicos vol.16
• Bertoin J. "Random Fragmentation and Coagulation Processes"., 2006. Cambridge Studies in Advanced Mathematics, 102. Cambridge University Press, Cambridge, 2006. ISBN 978-0-521-86728-3;
• Pitman J. "Combinatorial stochastic processes" Springer (2003)

Voci correlate

• Orologio molecolare
• Teoria neutrale dell'evoluzione
• Evoluzione
• Evoluzione umana
• Genetica delle popolazioni

Portale Biologia

Portale Matematica