Rivestimento (topologia)
Da Wikipedia, l'enciclopedia libera
Da Wikipedia, l'enciclopedia libera
Il rivestimento è una nozione centrale della topologia, importante per lo studio degli spazi topologici e delle funzioni continue fra questi. La nozione di rivestimento è strettamente collegata a quella di gruppo fondamentale.
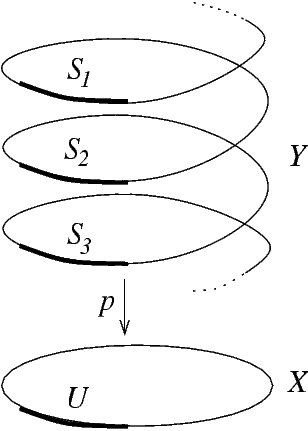
Un rivestimento è una funzione continua e suriettiva p : Y → X fra spazi topologici con la proprietà che ogni punto x in X ha un intorno aperto U la cui controimmagine in Y è unione di aperti disgiunti, tali che restringendo la p su ciascuno di questi si ottiene un omeomorfismo su U. Un tale aperto U è detto uniformemente rivestito.
Si dice anche che lo spazio Y riveste X tramite la mappa p. Generalmente per semplicità si chiede anche che X e Y siano entrambi connessi per archi, ed è quanto supposto in questa trattazione.
La controimmagine di un punto x è la fibra su x. La cardinalità della fibra non dipende dal punto x, ed è il numero di fogli o grado del rivestimento: può essere finito o infinito.
Consideriamo la circonferenza unitaria S1 in R2. Allora la funzione p : R → S1 data da
è un rivestimento con un numero infinito di fogli.
Denotiamo con C* il piano complesso senza l'origine 0. La mappa p : C* → C* data da
è un rivestimento a n fogli per ogni numero naturale positivo n.
Un rivestimento è un omeomorfismo locale. Non è vero il viceversa in generale: ad esempio, in un omeomorfismo locale la cardinalità della fibra su x può cambiare al variare di x.
Una definizione alternativa di rivestimento è la seguente: p: Y → X è un rivestimento se
Un rivestimento p: Y → X induce una funzione iniettiva sui gruppi fondamentali p*: π1(Y,y) → π1(X,x), per ogni x e y tali che x = p(y).
Il numero di fogli di un rivestimento è pari all'indice del sottogruppo p*(π1(Y,y)) dentro π1(X,x).
Se X è uno spazio topologico localmente semplicemente connesso (e tutti gli spazi topologici "buoni" soddisfano questa proprietà), per ogni sottogruppo H di π1(X,x) esistono uno spazio Y ed un rivestimento p:Y → X tali che l'immagine di p*: π1(Y,y) → π1(X,x) sia proprio H. Tale rivestimento è unico a meno di isomorfismi (definiti opportunamente).
Un rivestimento induce degli isomorfismi sui gruppi di omotopia superiori al primo. Se ne deduce quindi ad esempio che
per ogni n > 1, poiché R è contrattile.
Ogni struttura locale di X è ereditata tramite p dallo spazio Y che lo riveste:
Se Y è compatto, allora il rivestimento ha grado finito. Questo perché la controimmagine di un punto di X è un insieme discreto in Y, ed un insieme discreto e chiuso in un compatto è finito.
Più in generale, se X è compatto, allora Y è compatto se e solo se il rivestimento ha grado finito.
Il grado d di un rivestimento p: Y → X e la caratteristica di Eulero dei due spazi topologici sono collegati dalla relazione seguente:
Nella trattazione che segue, si suppone per semplicità che gli spazi cui si fa riferimento siano connessi per archi e localmente semplicemente connessi: queste due proprietà molto naturali sono soddisfatte da tutti gli spazi più studiati in topologia. Uno spazio che non le soddisfa contiene almeno un punto con degli intorni molto complicati, come ad esempio l'oggetto mostrato qui a destra.
Un rivestimento p:Y → X in cui Y è semplicemente connesso è detto un rivestimento universale di X. Le proprietà elencate precedentemente implicano che uno spazio topologico X ha un unico rivestimento universale (a meno di isomorfismi definiti opportunamente), e che il numero di fogli di p è pari alla cardinalità di π1(X,x).
L'esempio R → S1 descritto sopra è un rivestimento universale. L'altro esempio C* → C* invece non lo è, perché C* non è semplicemente connesso.
La mappa p: R2 → S1 x S1 data da
è un rivestimento con infiniti fogli sul toro, che è omeomorfo al prodotto S1 x S1.
La mappa p: Sn → Pn(R) data da
dalla sfera unitaria in Rn+1 allo spazio proiettivo reale, entrambi di dimensioni n, è un rivestimento con due fogli. Per n>1 la sfera è semplicemente connessa, e quindi è il rivestimento universale dello spazio proiettivo.
Ogni varietà non orientabile V è rivestita da una varietà orientabile, tramite un rivestimento doppio (cioè di grado 2). La varietà orientabile ha quindi caratteristica di Eulero doppia di quella di V.
In particolare, ogni superficie nello spazio avente una sola faccia (unilatera) è rivestita da una superficie con due facce (bilatera). Ad esempio, il nastro di Möbius è rivestito da un anello.
Molte superfici non orientabili non sono visualizzabili dentro lo spazio, mentre il loro rivestimento orientabile lo è: ad esempio la bottiglia di Klein è rivestita dal toro, ed Il piano proiettivo reale, per quanto appena visto, è rivestito dalla sfera.
Wikizionario contiene il lemma di dizionario «rivestimento»Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
