Reticolo di Bravais

In geometria e in cristallografia, un reticolo cristallino (o "reticolo di Bravais", dal francese Auguste Bravais che per primo lo descrisse nel 1848^[1]) è un insieme infinito di punti discreti aventi disposizione geometrica sempre uguale in tutto lo spazio. I punti del reticolo sono costituiti da una "base" (racchiusa all'interno di una cella unitaria), cioè da un insieme di uno o più entità molecolari (atomi, molecole o ioni), per cui la struttura atomica dei cristalli è definita dal reticolo e dalla base del reticolo.^[2]

I cinque reticoli cristallini in due dimensioni: obliquo, rettangolare, rettangolare centrato, esagonale e quadrato

La teoria dei gruppi permette di definire il numero di reticoli di Bravais possibili per ogni dimensione dello spazio.

Definizione

Si ponga l'origine degli assi cartesiani su un qualsiasi punto del reticolo, ogni punto è individuato da un vettore. Un reticolo di Bravais è generato da operazioni di traslazione nello spazio di un insieme di vettori, detti vettori primitivi. I vettori primitivi sono linearmente indipendenti e la loro scelta non è univoca.

La definizione generale di reticolo di Bravais ${\displaystyle \mathbf {R} }$ in ${\displaystyle d}$ dimensioni è:

${\displaystyle \mathbf {R} =\sum _{i=1}^{d}n_{i}\mathbf {a} _{i}}$

dove ${\displaystyle n_{i}}$sono numeri interi e ${\displaystyle \mathbf {a} _{i}}$ i vettori primitivi del reticolo.

Il reticolo in una dimensione è unico e definito dall'equazione:

${\displaystyle \mathbf {R} =n_{1}\mathbf {a} _{1}}$

In due dimensioni il reticolo viene definito dall'equazione:

${\displaystyle \mathbf {R} =n_{1}\mathbf {a} _{1}+n_{2}\mathbf {a} _{2}}$

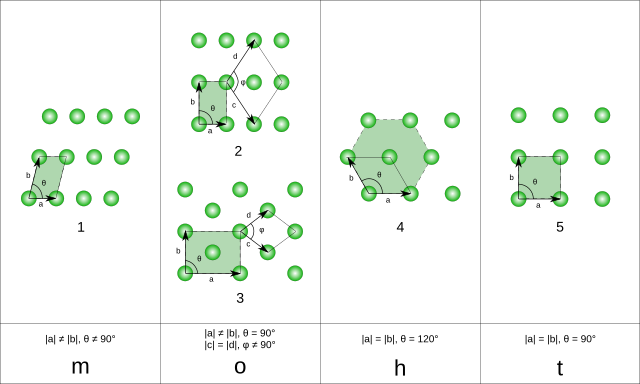
con ${\displaystyle \mathbf {a} _{1}}$ e ${\displaystyle \mathbf {a} _{2}}$, i vettori primitivi, che non sono paralleli. In due dimensioni esistono cinque reticoli di Bravais: obliquo, rettangolare, rettangolare centrato, esagonale e quadrato. In realtà vi sono quattro sistemi cristallini, in quanto il rettangolare e il rettangolare centrato appartengono allo stesso sistema cristallino.

Il reticolo in tre dimensioni viene definito dall'equazione:

${\displaystyle \mathbf {R} =n_{1}\mathbf {a} _{1}+n_{2}\mathbf {a} _{2}+n_{3}\mathbf {a} _{3}}$

con ${\displaystyle \mathbf {a} _{1}}$, ${\displaystyle \mathbf {a} _{2}}$ e ${\displaystyle \mathbf {a} _{3}}$ i vettori primitivi, che non sono complanari.

Cella primitiva

Lo stesso argomento in dettaglio: Cella primitiva.

Si definisce cella primitiva unitaria di un reticolo un volume di spazio che, traslato attraverso tutti i vettori di un reticolo di Bravais, riempie completamente il reticolo senza sovrapposizioni e senza lasciare spazi vuoti. Una cella primitiva contiene un solo punto del reticolo, e ha stessa simmetria del reticolo.

Nel caso tridimensionale, conoscendo il volume, è possibile determinare la densità del solido:

${\displaystyle n={\frac {m}{V}}}$

Dove ${\displaystyle m}$ è la massa della base e ${\displaystyle V\ }$ è il volume della cella unitaria. Da un punto di vista geometrico si dimostra che, detti ${\displaystyle \mathbf {a} _{1}}$, ${\displaystyle \mathbf {a} _{2}}$, ${\displaystyle \mathbf {a} _{3}}$ i vettori primitivi, il volume della cella unitaria risulta:

${\displaystyle V=\mathbf {a} _{1}\cdot \mathbf {a} _{2}\times \mathbf {a} _{3}}$

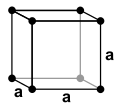
Nel caso tridimensionale per un reticolo ${\displaystyle sc}$ la scelta più banale è quella di un cubo di lato ${\displaystyle a}$.

Tutto lo spazio di un reticolo può essere riempito con celle convenzionali senza sovrapposizioni quando viene traslato attraverso un sottoinsieme dei vettori del reticolo di Bravais.

Costruzione della cella di Wigner-Seitz per un reticolo di Bravais esagonale (bididimensionale)

Cella primitiva di Wigner-Seitz

Lo stesso argomento in dettaglio: Cella di Wigner-Seitz.

La cella di Wigner-Seitz attorno a un punto di un reticolo di Bravais è la cella primitiva che gode di tutte le proprietà di simmetria della struttura.

Reticolo reciproco

Lo stesso argomento in dettaglio: Reticolo reciproco.

Consideriamo un set di punti ${\displaystyle \mathbf {R} }$ che costituiscono un reticolo di Bravais e un'onda piana, definita da ${\displaystyle e^{i\mathbf {k} \cdot \mathbf {r} }}$. Tale onda, per alcuni valori di ${\displaystyle \mathbf {k} }$, ha la periodicità del reticolo di Bravais. L'insieme dei vettori d'onda ${\displaystyle \mathbf {K} }$ che descrive onde piane con la periodicità di un dato reticolo di Bravais si chiama reticolo reciproco. Tale condizione da un punto di vista algebrico corrisponde a scrivere:

${\displaystyle e^{i\mathbf {K} \cdot (\mathbf {r} +\mathbf {R} )}=e^{i\mathbf {K} \cdot \mathbf {r} }}$

Dovendo tale relazione valere per qualsiasi ${\displaystyle \mathbf {r} }$ segue che l'insieme dei vettori del reticolo reciproco soddisfa la relazione:

${\displaystyle e^{i\mathbf {K} \cdot \mathbf {R} }=1}$

per tutti i punti ${\displaystyle \mathbf {R} }$ del reticolo di Bravais.

Classificazione

I reticoli di Bravais si classificano in base alla forma della cella convenzionale, dove ciascuna forma corrisponde a uno dei sette sistemi cristallini, e alla presenza o meno di punti del reticolo al centro del corpo o delle facce di questa.

I sette sistemi cristallini sono:

• cubico;
• tetragonale;
• ortorombico;
• monoclino;
• triclino;
• esagonale;
• romboedrico (o trigonale).

e la centratura del reticolo può essere:

• primitiva (${\displaystyle P}$): nessun punto oltre ai vertici della cella;
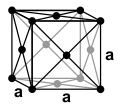
• a corpo centrato (${\displaystyle I}$): un punto al centro della cella;
• a facce centrate (${\displaystyle F}$): un punto al centro di ogni faccia;
• con una faccia centrata (${\displaystyle A}$, ${\displaystyle B}$ o ${\displaystyle C}$): un punto al centro delle due facce in una sola direzione.

Non tutte le combinazioni sistema cristallino-centratura danno però luogo a differenti tipi di reticolo, in quanto alcune di queste sono equivalenti: ad esempio, un reticolo monoclino I è equivalente a un reticolo monoclino C cambiando la scelta dei vettori di base.

In tre dimensioni vi sono 14 tipi di reticolo di Bravais,^[1] riportati di seguito. Per quanto riguarda la sigla con cui vengono identificati si usa normalmente la notazione che deriva dall'inglese.

Reticolo di Bravais	Sistema cristallino	Cella convenzionale	${\displaystyle V_{C}/V_{P}}$[N 1]	Generatori	Caratteristiche	Sigla
Cubico P (semplice)	Cubico ${\displaystyle a=b=c}$ ${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$		1	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}=c}$	Il lato della cella è pari al doppio del raggio atomico dell'elemento considerato; si può pensare che gli atomi siano rappresentati da sferette rigide e che la cella elementare sia formata da sferette a contatto lungo gli spigoli del cubo. Il rapporto tra lo spazio occupato dalle sferette e il volume della cella dà il fattore di impaccamento di 0,52.	sc
Cubico I (a corpo centrato)			2	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}={\frac {(a+b+c)}{2}}}$	la struttura cubica a corpo centrato contiene un atomo all'interno della struttura cubica. Le sferette sono a contatto solo lungo le diagonali della cella cubica. Il fattore di impaccamento è 0,68.	bcc
Cubico F (a facce centrate)			4	${\displaystyle \mathbf {a} _{1}={\frac {(a+b)}{2}}}$ ${\displaystyle \mathbf {a} _{2}={\frac {(a+c)}{2}}}$ ${\displaystyle \mathbf {a} _{3}={\frac {(b+c)}{2}}}$	La struttura cubica a facce centrate è costituita da celle elementari che contengono su ogni faccia della struttura cubica un atomo. Il parametro reticolare si allarga ancora rispetto alle precedenti. Il fattore di impaccamento è 0,74.	fcc
Tetragonale P (semplice)	Tetragonale ${\displaystyle a=b}$ ${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$		1	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}=c}$		st
Tetragonale I (a corpo centrato)			2	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}={\frac {(a+b+c)}{2}}}$		bct
Ortorombico P (semplice)	Ortorombico ${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$		1	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}=c}$		so
Ortorombico I (a corpo centrato)			2	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}={\frac {(a+b+c)}{2}}}$		orc
Ortorombico F (a facce centrate)			4	${\displaystyle \mathbf {a} _{1}={\frac {(a+b)}{2}}}$ ${\displaystyle \mathbf {a} _{2}={\frac {(a+c)}{2}}}$ ${\displaystyle \mathbf {a} _{3}={\frac {(b+c)}{2}}}$		orc
Ortorombico C (a base centrata)			2	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}={\frac {(a+b)}{2}}}$ ${\displaystyle \mathbf {a} _{3}=c}$		orc
Monoclino P (semplice)	Monoclino ${\displaystyle \alpha =\gamma =90^{\circ }}$		1	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}=c}$		mcl
Monoclino C (a base centrata)			2	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}={\frac {(a+b)}{2}}}$ ${\displaystyle \mathbf {a} _{3}=c}$		mcl
Triclino	Triclino ${\displaystyle a\neq b\neq c}$		1	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}=c}$
Esagonale	Esagonale ${\displaystyle a=b}$ ${\displaystyle \alpha =\beta =90^{\circ },\gamma =120^{\circ }}$		3	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}=c}$	Le facce superiore e inferiore della cella esagonale hanno un atomo al centro. Su un piano intermedio tra queste due facce sono situati tre atomi disposti a triangolo. Le tre sferette del piano intermedio sono a contatto con quelle delle facce superiore e inferiore. Il fattore di impaccamento è 0,74.	hex
Romboedrico (o trigonale)	Romboedrico (o trigonale)[N 2] ${\displaystyle a=b=c}$		1	${\displaystyle \mathbf {a} _{1}=a}$ ${\displaystyle \mathbf {a} _{2}=b}$ ${\displaystyle \mathbf {a} _{3}=c}$		hex

Numero di coordinazione

Si chiamano primi vicini i punti del reticolo più vicini a un dato punto del reticolo stesso. A causa della natura periodica del reticolo di Bravais ogni punto ha lo stesso numero di primi vicini. Si chiama numero di coordinazione il numero di primi vicini, tale grandezza è una proprietà fondamentale del reticolo. In tabella sono dati i numeri di coordinazione dei tre reticoli cubici assieme ad altre proprietà di tale reticoli.

Reticolo	N. coordinazione	Distanza primi vicini	Elementi per cella conv.
sc	6	${\displaystyle a}$	1
bcc	8	${\displaystyle a{\sqrt {3}}/2}$	2
fcc	12	${\displaystyle a/{\sqrt {2}}}$	4

Esempi di struttura cristallina

Nella tabella sono riportati i tipi di struttura cristallina per gli elementi metallici più importanti. La distanza interatomica si riferisce alla distanza fra due atomi dello stesso elemento misurata con l'aiuto della diffrazione a raggi X.

Metallo	Struttura	Distanza interatomica (nm)	Raggio atomico (nm)
Argento	fcc	0,2888	0,1444
Alluminio	fcc	0,2862	0,1431
Oro	fcc	0,2882	0,1441
Berillio	hex	0,228	0,114
Cadmio	hex	0,296	0,158
Cobalto	hex	0,250	0,125
Cromo	bcc	0,2498	0,1249
Rame	fcc	0,2556	0,1278
Ferro\alpha	bcc	0,2482	0,1241
Ferro\gamma	fcc	0,2540	0,1270
Potassio	bcc	0,4624	0,2312
Litio	bcc	0,3038	0,1519
Magnesio	hex	0,322	0,161
Molibdeno	bcc	0,2725	0,1362
Sodio	bcc	0,3174	0,1857
Nichel	fcc	0,2491	0,1246
Piombo	fcc	0,3499	0,1750
Platino	fcc	0,2775	0,1386
Titanio \alfa	hex	0,293	0,164
Titanio \beta	bcc	0,285	0,142
Vanadio	bcc	0,2362	0,1316
Wolframio (tungsteno)	bcc	0,2734	0,1367
Zinco	hex	0,278	0,139
Zirconio	hex	0,324	0,162