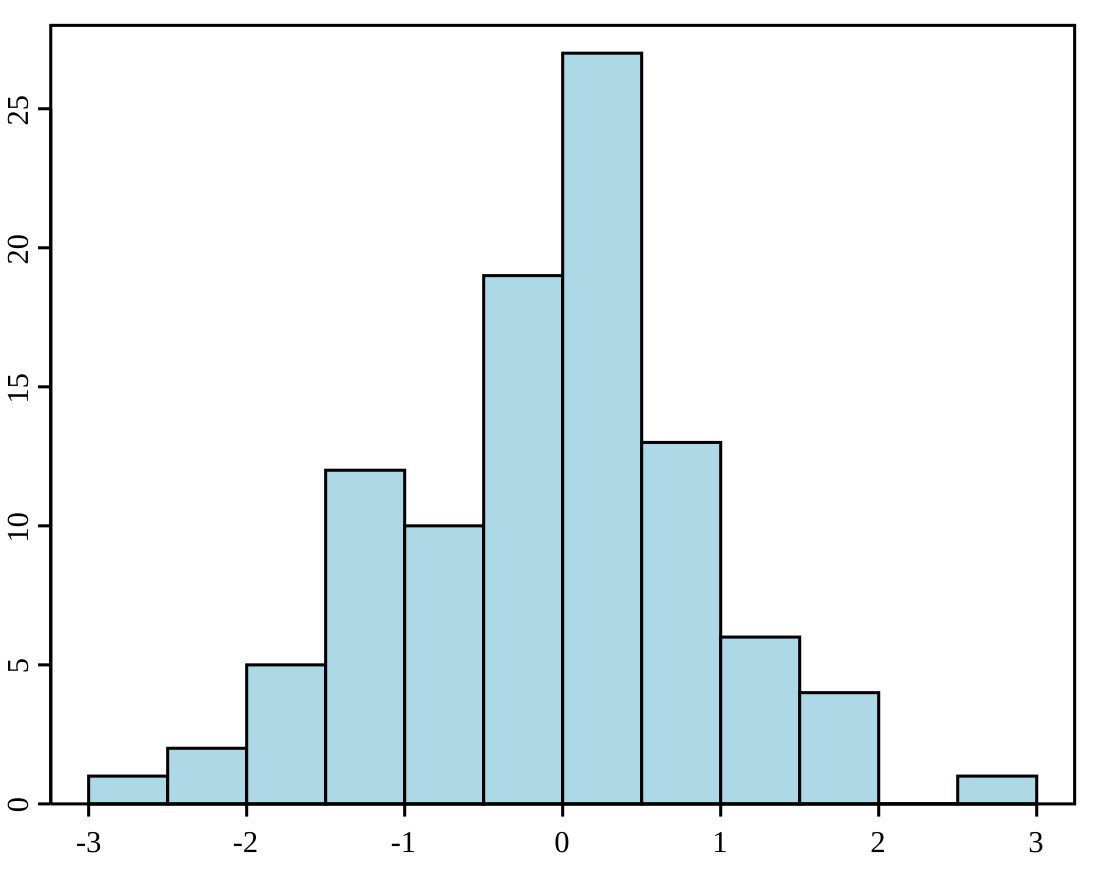
Istogramma
Da Wikipedia, l'enciclopedia libera
L'istogramma è la rappresentazione grafica (diagramma) di una distribuzione in classi di un carattere continuo.

Descrizione dell'istogramma
Riepilogo
Prospettiva
L'istogramma è costituito da rettangoli adiacenti, le cui basi sono allineate su un asse orientato e dotato di unità di misura (l'asse ha l'unità di misura del carattere e può essere inteso come l'asse delle ascisse). L'adiacenza dei rettangoli dà conto della continuità del carattere. Ogni rettangolo ha base di lunghezza pari all'ampiezza della corrispondente classe; l'altezza invece è calcolata come densità di frequenza, ossia è pari al rapporto fra la frequenza (assoluta) associata alla classe e l'ampiezza della classe.[1]
L'area della superficie di ogni rettangolo coincide con la frequenza associata alla classe cui il rettangolo si riferisce e per tale caratteristica gli istogrammi rappresentano un tipo di areogramma. La somma delle aree dei rettangoli è uguale alla somma delle frequenze dei valori appartenenti alle varie classi.
Volendo si può scegliere di rappresentare nell'istogramma le frequenze relative (anziché le semplici frequenze assolute) delle varie classi.
Dividendo le frequenze relative di un istogramma per l'ampiezza di ciascuna classe si attuerà un processo di normalizzazione dell'istogramma ottenendo così un istogramma di densità, la cui somma delle aree delle ampiezze di ciascuna classe rappresentata sarà uguale ad 1.
Nell'ipotesi che la numerosità dei valori osservati tenda a infinito, e contemporaneamente l'ampiezza delle classi tenda a zero, l'istogramma converge, a sua volta, a una stima (seppur distorta) della legge di probabilità che regola l'esperimento casuale da cui si osserva il carattere.
Gli istogrammi non devono essere confusi con i grafici a colonne: questi ultimi infatti, a differenza dei primi, hanno altezza proporzionale alla frequenza e sono costituiti da rettangoli separati tra loro.
Gli istogrammi vengono spesso utilizzati nella fotografia digitale e nel fotoritocco per analizzare la luminosità di un'immagine.
Note
Voci correlate
Altri progetti
Collegamenti esterni
Wikiwand - on
Seamless Wikipedia browsing. On steroids.