Equazioni di Fridman

Le equazioni di Fridmann sono un insieme di equazioni in cosmologia fisica che governano l'espansione dello spazio in modelli omogenei e isotropi dell'universo nel contesto della relatività generale. Sono state derivate per la prima volta da Aleksandr Fridman nel 1922 dall'equazione di campo di Einstein della gravità nella metrica di Friedmann-Lemaître-Robertson-Walker e un fluido perfetto con una data densità di massa ${\displaystyle \rho }$ e pressione ${\displaystyle p}$.^[1] Le equazioni per la curvatura spaziale negativa sono ricavate da Fridman nel 1924.^[2]

Aleksandr Fridman

Assunzioni

Per ricavare le equazioni di Fridmann bisogna assumere che l'universo sia spazialmente omogeneo e isotropo (cioè assumere il principio cosmologico); empiricamente, questo è ragionevole su scale maggiori di ~100 Mpc. Il principio cosmologico implica che la metrica dell'universo debba essere della forma

${\displaystyle ds^{2}=a(t)^{2}\,ds_{3}^{2}-c^{2}\,dt^{2}}$

dove ${\displaystyle ds_{3}^{2}}$ è una metrica tridimensionale che deve essere o (a) spazio piatto, (b) una sfera di curvatura costante positiva oppure (c) uno spazio iperbolico con curvatura costante negativa. Questa è la metrica di Friedmann–Lemaître–Robertson–Walker (FLRW). Il parametro ${\displaystyle k}$ discusso sotto, a seconda del tipo di spazio, assume i valori della curvatura gaussiana corrispondente, rispettivamente 0, 1, −1. È questo fatto che permette di dare un senso al "fattore di scala" ${\displaystyle a(t)}$.

Le equazioni di Einstein ora mettono in relazione l'evoluzione di questo fattore di scala con la pressione e l'energia della materia dell'universo. Dalla metrica FLRW si possono calcolare i simboli di Christoffel e quindi il tensore di Ricci. Da questi, con il tensore energia-impulso per un fluido perfetto, si ottengono dalle equazioni di campo di Einstein le equazioni descritte di seguito.

Equazioni

Ci sono due equazioni di Friedmann indipendenti per modellizzare un universo omogeneo e isotropo. La prima è:

${\displaystyle {\frac {{\dot {a}}^{2}+kc^{2}}{a^{2}}}={\frac {8\pi G\rho +\Lambda c^{2}}{3}}}$

che si ricava dalla componente 00 dell'equazione di campo di Einstein. La seconda è:

${\displaystyle {\frac {\ddot {a}}{a}}=-{\frac {4\pi G}{3}}\left(\rho +{\frac {3p}{c^{2}}}\right)+{\frac {\Lambda c^{2}}{3}}}$

che si ricava dalla prima insieme alla traccia dell'equazione di campo (la dimensione delle due equazioni è tempo⁻²).

In queste equazioni ${\displaystyle a}$ è il fattore di scala, G, Λ, e c sono costanti universali (G è la costante di gravitazione universale, Λ è la costante cosmologica (dimensioni lunghezza⁻²) e c è la velocità della luce nel vuoto). ρ e p sono rispettivamente la densità di massa volumetrica (non la densità di energia) e la pressione. k è costante fissata una certa soluzione, ma varia a seconda della soluzione.

Nelle equazioni precedenti, ${\displaystyle a}$, ρ, e p sono funzioni del tempo. ${\displaystyle {\tfrac {k}{a^{2}}}}$ è la curvatura spaziale in un certo istante temporale dell'universo; è pari a un sesto dello scalare di Ricci spaziale dato che nel modello spaziotemporale di Friedmann

${\displaystyle R={\frac {6}{c^{2}a^{2}}}({\ddot {a}}a+{\dot {a}}^{2}+kc^{2})}$

Il rapporto ${\displaystyle H\equiv {\tfrac {\dot {a}}{a}}}$ è detto parametro di Hubble.

Si nota che nelle equazioni di Friedmann, ${\displaystyle a(t)}$ non dipende dal sistema di coordinate scelto a istante fissato. Ci sono due scelte comuni per ${\displaystyle a}$ e ${\displaystyle k}$ che descrivono la stessa fisica:

• k = +1, 0 o −1 a seconda che la forma dell'universo sia rispettivamente una 3-sfera chiusa, piatta (cioè lo spazio euclideo) o un 3-iperboloide aperto.^[3] Se k = +1, allora ${\displaystyle a}$ è il raggio di curvatura dell'universo, Se k = 0, allora ${\displaystyle a}$ può essere fissato a un numero positivo a un particolare tempo. Se k = −1, allora si può dire (approssimativamente) che ${\displaystyle i}$·${\displaystyle a}$ è il raggio di curvatura dell'universo.
• ${\displaystyle a}$ è il fattore di scala che si pone a 1 al tempo presente. ${\displaystyle k}$ è la curvatura spaziale quando ${\displaystyle a=1}$ (cioè al tempo presente). Se la forma dell'universo è ipersferica e ${\displaystyle R_{t}}$ è il raggio di curvatura (${\displaystyle R_{0}}$ al tempo presente), allora ${\displaystyle a=R_{t}/R_{0}}$. Se ${\displaystyle k}$ è positivo, allora l'universo è ipersferico. Se ${\displaystyle k}$ è zero, allora l'universo è piatto. Se ${\displaystyle k}$ è negativo, allora l'universo è iperbolico.

Usando la prima equazione, si può riscrivere la seconda equazione come

${\displaystyle {\dot {\rho }}=-3H\left(\rho +{\frac {p}{c^{2}}}\right),}$

che elimina ${\displaystyle \Lambda }$ e esprime la conservazione della massa-energia ${\displaystyle T^{\alpha \beta }{}_{;\beta }\,=0}$.

Queste equazioni sono a volte semplificate sostituendo

${\displaystyle \rho \rightarrow \rho -{\frac {\Lambda c^{2}}{8\pi G}}}$

${\displaystyle p\rightarrow p+{\frac {\Lambda c^{4}}{8\pi G}}}$

per dare:

${\displaystyle H^{2}=\left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}}$

${\displaystyle {\dot {H}}+H^{2}={\frac {\ddot {a}}{a}}=-{\frac {4\pi G}{3}}\left(\rho +{\frac {3p}{c^{2}}}\right).}$

La forma semplificata della seconda equazione è invariante sotto questa trasformazione.

Il parametro di Hubble può cambiare nel tempo se altre parti dell'equazione sono dipendenti dal tempo (in particolare la densità di massa, l'energia del vuoto o la curvatura spaziale). Calcolare il parametro di Hubble al tempo attuale dà la costante di Hubble che è la costante di proporzionalità della legge di Hubble. Applicata a un fluido con una data equazione di stato, le equazioni di Friedmann danno l'evoluzione temporale e la geometria dell'universo in funzione della densità del fluido.

Alcuni cosmologi chiamano la seconda di queste due equazioni l'equazione di Friedmann sull'accelerazione e riservano il termine equazione di Friedmann solo per la prima equazione.

Parametro densità

Il parametro densità ${\displaystyle \Omega }$ è definito come il rapporto della densità reale (o osservata) ${\displaystyle \rho }$ con la densità critica ${\displaystyle \rho _{c}}$ dell'universo di Friedmann. La relazione tra la densità reale e la densità critica determina la generale geometria dell'universo; dove sono uguali, la geometria dell'universo è piatta (euclidea). In modelli primitivi, che non includeva il termine della costante cosmologica, la densità critica era inizialmente definita come il punto spartiacque tra un universo in espansione e uno in contrazione.

Attualmente, si stima che la densità critica sia approssimativamente di 5 atomi (idrogeno monatomico) per metro cubo, mentre si crede che la densità media della materia ordinaria (barionica) nell'universo sia circa di 0,2–0,25 atomi per metro cubo.^[4][5]

La stimata distribuzione relativa delle componenti della densità di energia dell'universo. L'energia oscura domina l'energia totale (74%) mentre la materia oscura (22%) costituisce la maggior parte della massa. Della rimanente materia barionica (4%), solo un decimo è compatto. A febbraio 2015, il team di ricerca europeo dietro alla sonda Planck Surveyor pubblicò nuovi dati precisando questi valori a 4.9% per la materia ordinaria, 25.9% per la materia oscura e il 69.1% per l'energia oscura.

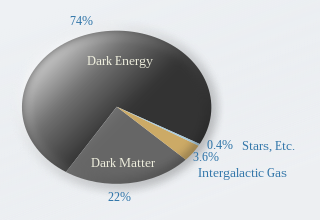
Una densità molto maggiore viene dall'ignota materia oscura; sia la materia ordinaria sia quella oscura contribuisce in favore della contrazione dell'universo. Tuttavia, la parte più grande viene dalla cosiddetta energia oscura, che tiene conto del termine della costante cosmologica. Sebbene la densità totale è uguale alla densità critica (più precisamente, a meno di errore di misurazione), l'energia oscura non porta alla contrazione dell'universo ma piuttosto potrebbe accelerare la sua espansione. Quindi, l'universo potrebbe espandersi per sempre.

Si può trovare un'espressione per la densità critica assumendo nulla la costante cosmologica Λ (come vale per tutti gli universi di Friedmann) e ponendo la curvatura spaziale normalizzata, k, pari a zero. Quando le sostituzioni sono applicate alla prima delle equazioni di Friedmann si ottiene:

${\displaystyle \rho _{c}={\frac {3H^{2}}{8\pi G}}=1.8788\times 10^{-26}h^{2}{\rm {kg}}\,{\rm {m}}^{-3}=2.7754\times 10^{11}h^{2}M_{\odot }\,{\rm {Mpc}}^{-3},}$

(dove h = H_o/(100 km/s/Mpc). For H_o = 67.4 km/s/Mpc, cioè h = 0.674, ρ_c = 8.5 × 10⁻²⁷ kg/m³)

Il parametro densità (utile per paragonare modelli cosmologici diversi) è quindi definito come:

${\displaystyle \Omega \equiv {\frac {\rho }{\rho _{c}}}={\frac {8\pi G\rho }{3H^{2}}}.}$

La prima equazione di Friedmann è spesso vista in termini dei valori attuali dei parametri di densità, cioè^[6]

${\displaystyle {\frac {H^{2}}{H_{0}^{2}}}=\Omega _{0,R}a^{-4}+\Omega _{0,M}a^{-3}+\Omega _{0,k}a^{-2}+\Omega _{0,\Lambda }.}$

Qui ${\displaystyle \Omega _{0,R}}$ è la densità di radiazione attuale (ossia quando ${\displaystyle a=1}$), ${\displaystyle \Omega _{0,M}}$ è la densità di materia (oscura più barionica) attuale, ${\displaystyle \Omega _{0,k}=1-\Omega _{0}}$ è la "densità di curvatura spaziale" attuale, e ${\displaystyle \Omega _{0,\Lambda }}$ è la costante cosmologica o l'attuale densità del vuoto.

Soluzioni utili

Le equazioni di Friedmann possono essere risolte esattamente in presenza di un fluido perfetto con l'equazione di stato

${\displaystyle p=w\rho c^{2},}$

dove ${\displaystyle p}$ è la pressione, ${\displaystyle \rho }$ è la densità di massa del fluido nel sistema di riferimento comovente e ${\displaystyle w}$ è una certa costante.

Nel caso spazialmente piatto (k = 0), la soluzione per il fattore di scala è

${\displaystyle a(t)=a_{0}\,t^{\frac {2}{3(w+1)}}}$

dove ${\displaystyle a_{0}}$ è una certa costante di integrazione da fissare con la scelta delle condizioni iniziali. Questa famiglia di soluzioni etichettate da ${\displaystyle w}$ è estremamente importante per la cosmologia. Ad esempio, ${\displaystyle w=0}$ descrive un universo dominato dalla materia, in cui la pressione è trascurabile rispetto alla densità di massa. Dalla soluzione generica si vede facilmente che in un universo dominato dalla materia il fattore di scala ha un andamento come

${\displaystyle a(t)\propto t^{2/3}}$

Un altro esempio importante è il caso di un universo dominato dalla radiazione, cioè quando ${\displaystyle w=1/3}$. Questo porta a

${\displaystyle a(t)\propto t^{1/2}}$

Si noti che questa soluzione non è valida per un universo dominato dalla costante cosmologica, che corrisponde a ${\displaystyle w=-1}$. In questo caso la densità di energia è costante e il fattore di scala cresce esponenzialmente.

Miscele

Se la materia è un misto di due o più fluidi non interagenti, ciascuno con la sua equazione di stato, allora

${\displaystyle {\dot {\rho }}_{f}=-3H\left(\rho _{f}+{\frac {p_{f}}{c^{2}}}\right)\,}$

vale separatamente per ogni fluido f. In ogni caso,

${\displaystyle {\dot {\rho }}_{f}=-3H\left(\rho _{f}+w_{f}\rho _{f}\right)\,}$

dalla quale si ottiene

${\displaystyle {\rho }_{f}\propto a^{-3(1+w_{f})}\,.}$

Ad esempio, si può formare una combinazione lineare di tali termini

${\displaystyle \rho =Aa^{-3}+Ba^{-4}+Ca^{0}\,}$

dove: A è la densità della "polvere" (materia ordinaria, w = 0) quando ${\displaystyle a=1}$; B è la densità della radiazione (w = 1/3) quando ${\displaystyle a=1}$; C è la densità della "energia oscura" (w = −1). Si sostituisce ciò in

${\displaystyle \left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}\,}$

e si risolve per ${\displaystyle a}$ in funzione del tempo.

Equazione di Friedmann riscalata

Si ponga ${\displaystyle {\tilde {a}}={\frac {a}{a_{0}}},\;\rho _{c}={\frac {3H_{0}^{2}}{8\pi G}},\;\Omega ={\frac {\rho }{\rho _{c}}},\;t={\frac {\tilde {t}}{H_{0}}},\;\Omega _{c}=-{\frac {kc^{2}}{H_{0}^{2}a_{0}^{2}}}\;}$, dove ${\displaystyle a_{0}}$ e ${\displaystyle H_{0}}$ sono rispettivamente il fattore di scala e il parametro di Hubble nel presente. Allora si ha

${\displaystyle {\frac {1}{2}}\left({\frac {d{\tilde {a}}}{d{\tilde {t}}}}\right)^{2}+U_{\text{eff}}({\tilde {a}})={\frac {1}{2}}\Omega _{c}}$

dove ${\displaystyle U_{\text{eff}}({\tilde {a}})={\frac {-\Omega {\tilde {a}}^{2}}{2}}\;}$. Per ogni forma del potenziale efficace ${\displaystyle U_{\text{eff}}({\tilde {a}})\;}$, c'è un'equazione di stato ${\displaystyle p=p(\rho )}$ che lo produrrà.

Note

1. (DE) A. Friedman, Über die Krümmung des Raumes, in Z. Phys., vol. 10, n. 1, 1922, pp. 377–386, Bibcode:1922ZPhy...10..377F, DOI:10.1007/BF01332580. (Traduzione inglese: A Friedman, On the Curvature of Space, in General Relativity and Gravitation, vol. 31, n. 12, 1999, pp. 1991–2000, Bibcode:1999GReGr..31.1991F, DOI:10.1023/A:1026751225741.). Il manoscritto russo originale è preservato nell'archivio di Ehrenfest.
2. (DE) A Friedmann, Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes, in Z. Phys., vol. 21, n. 1, 1924, pp. 326–332, Bibcode:1924ZPhy...21..326F, DOI:10.1007/BF01328280. (Traduzione inglese: A Friedmann, On the Possibility of a World with Constant Negative Curvature of Space, in General Relativity and Gravitation, vol. 31, n. 12, 1999, pp. 2001–2008, Bibcode:1999GReGr..31.2001F, DOI:10.1023/A:1026755309811.)
3. Ray A d'Inverno, Introducing Einstein's Relativity, ISBN 0-19-859686-3.
4. Rees, M., Just Six Numbers, (2000) Orion Books, Londra, p. 81, p. 82^{[non chiaro]}
5. What is the Universe Made Of?, su map.gsfc.nasa.gov.
   

   «The actual density of atoms is equivalent to roughly 1 proton per 4 cubic meters.»
6. Robert J. Nemiroff e Patla, Bijunath, Adventures in Friedmann cosmology: A detailed expansion of the cosmological Friedmann equations, in American Journal of Physics, vol. 76, p. 265, Bibcode:2008AmJPh..76..265N, DOI:10.1119/1.2830536, arXiv:astro-ph/0703739.

Bibliografia

• Dierck-Ekkehard Liebscher, Expansion, in Cosmology, Berlin, Springer, 2005, pp. 53–77, ISBN 3-540-23261-3.

Voci correlate

• Matematica della relatività generale

Portale Astronomia

Portale Fisica