Equazione di Korteweg-de Vries

In fisica matematica, l'equazione di Korteweg-de Vries (abbreviata in KdV) è un'equazione differenziale alle derivate parziali nonlineare utilizzata per modellare, tra le altre cose, le onde marine. Il sistema da essa descritto è integrabile.

Introdotta inizialmente da Joseph Boussinesq nel 1877^[1], fu poi riscoperta da Diderik Korteweg e Gustav de Vries nel 1895.^[2][3]

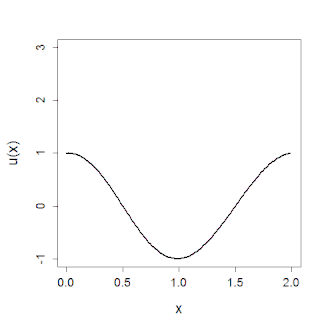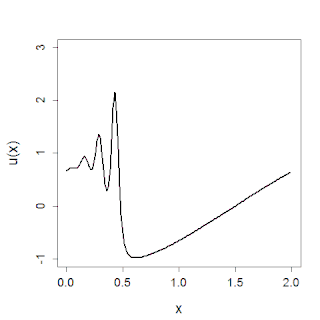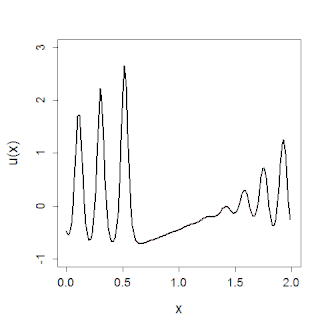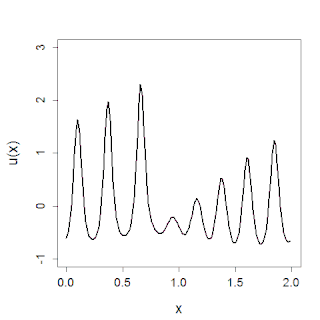
Lo studio dell'equazione si è notevolmente sviluppato dopo che Norman Zabusky e Martin D. Kruskal (1965) scoprirono, attraverso un algoritmo di integrazione numerica dell'equazione, la scomposizione delle soluzioni in solitoni. L'equazione ha trovato un gran numero di applicazioni alla fisica e ad altre scienze: dalle onde marine ai periodi di piena dei fiumi, fino alle onde sonore nei plasmi e nei cristalli. Può essere inoltre ottenuta nel limite continuo del problema di Fermi-Pasta-Ulam-Tsingou.

Soluzione di onda cnoidale per l'equazione di Korteweg–de Vries, in termini del quadrato della funzione ellittica di Jacobi ${\displaystyle \mathrm {cn} }$ con parametro ${\displaystyle m=0.9}$.

Soluzione numerica dell'equazione KdV ${\displaystyle u_{t}+uu_{x}+\delta ^{2}u_{xxx}=0}$ (${\displaystyle \delta =0.022}$) con condizione iniziale ${\displaystyle u(x,0)=\cos(\pi x)}$. Il calcolo è stato effettuato con il metodo di Zabusky-Kruskal.^[4] L'onda cosinusoidale iniziale evolve in un pacchetto di onde solitoniche.

Definizione

La KdV è un'equazione nonlineare e dispersiva per una funzione ${\displaystyle \phi }$ a due variabili (spaziale e temporale):^[5]

${\displaystyle \partial _{t}\phi +\partial _{x}^{3}\phi +6\,\phi \,\partial _{x}\phi =0\,}$

In cui ${\displaystyle \partial _{x}}$ e ${\displaystyle \partial _{t}}$ indicano le derivate parziali rispetto a ${\displaystyle x}$ e a ${\displaystyle t}$.

La costante ${\displaystyle 6}$ posta di fronte all'ultimo termine è presente per ragioni storiche, ma può essere semplicemente eliminata riscalando le variabili.

L'equazione KdV può essere ricavata a partire da quella di Boussinesq, imponendo un verso preciso nella propagazione dell'onda.

Solitoni

Soluzioni in cui un'onda di forma data ${\displaystyle f(X)}$ mantiene la propria geometria spostandosi con velocità di fase ${\displaystyle c}$ sono dette solitoni. Tali soluzioni si scrivono nella forma

${\displaystyle \phi (x,t)=f(x-ct-a)=f(X)}$

Sostituendo nella KdV si ottiene l'equazione differenziale ordinaria

${\displaystyle -c{\frac {df}{dX}}+{\frac {d^{3}f}{dX^{3}}}+6f{\frac {df}{dX}}=0}$

o, integrando rispetto a ${\displaystyle X}$,

${\displaystyle -cf+{\frac {d^{2}f}{dX^{2}}}+3f^{2}=A}$

dove ${\displaystyle A}$ è una costante d'integrazione. Interpretando la variabile ${\displaystyle X}$ come un parametro temporale, la funzione ${\displaystyle f}$ soddisfa l'Equazione del moto di Newton per una particella di massa unitaria in presenza di un potenziale cubico.

${\displaystyle V(f)=-(f^{3}+{\frac {1}{2}}cf^{2}+Af)}$

Se i parametri vengono impostati in modo tale che il potenziale ${\displaystyle V(f)}$ ha massimo locale per ${\displaystyle f=0}$ esiste una soluzione in cui ${\displaystyle f(X)}$ partendo da ${\displaystyle X=-\inf }$, scorre verso il minimo locale, poi riprende dall'altro lato, raggiungendo lo stesso valore, quindi torna indietro al massimo locale al tempo ${\displaystyle X=\inf }$. In altre parole, ${\displaystyle f(X)\to 0}$ per ${\displaystyle X\to \infty }$. Questa è la forma caratteristica del solitone^[6]

Si può dimostrare che la soluzione vale

${\displaystyle \phi (x,t)={\frac {1}{2}}\,c\,\mathrm {sech} ^{2}\left[{{\sqrt {c}} \over 2}(x-c\,t-a)\right]}$

dove ${\displaystyle \mathrm {sech} (x)}$ è la secante iperbolica e ${\displaystyle a}$ è una costante arbitraria.^[7] Questo è un solitone che si propaga verso destra.

Integrali del moto

La KdV ha un numero infinito di integrali primi^[8], costanti nel tempo. Essi si scrivono

${\displaystyle \int _{-\infty }^{+\infty }P_{2n-1}(\phi ,\,\partial _{x}\phi ,\,\partial _{x}^{2}\phi ,\,\ldots )\,{\text{d}}x\,}$

dove i polinomi ${\displaystyle P_{n}}$ sono definiti ricorsivamente

${\displaystyle {\begin{aligned}P_{1}&=\phi ,\\P_{n}&=-{\frac {dP_{n-1}}{dx}}+\sum _{i=1}^{n-2}\,P_{i}\,P_{n-1-i}\quad {\text{ per }}n\geq 2.\end{aligned}}}$

I primi integrali del moto sono dunque:

• la massa ${\displaystyle \int \phi \,{\text{d}}x,}$
• la quantità di moto ${\displaystyle \int \phi ^{2}\,{\text{d}}x,}$
• l'energia ${\displaystyle \int {\frac {1}{3}}\phi ^{3}-\left(\partial _{x}\phi \right)^{2}\,{\text{d}}x.}$

Solo i polinomi di indice dispari (${\displaystyle P_{2n+1}}$) corrispondono a integrali non-banali (diversi da zero)^[9].

Coppie di Lax

L'equazione KdV

${\displaystyle \partial _{t}\phi =6\,\phi \,\partial _{x}\phi -\partial _{x}^{3}\phi }$

può essere riformulata in termini dell'equazione di Lax

${\displaystyle L_{t}=[L,A]\equiv LA-AL\,}$

in cui L è un operatore di Sturm–Liouville:

${\displaystyle {\begin{aligned}L&=-\partial _{x}^{2}+\phi ,\\A&=4\partial _{x}^{3}-3\left[2\phi \,\partial _{x}+(\partial _{x}\phi )\right]\end{aligned}}}$

e questo vale per ognuno degli infiniti integrali dell'equazione KdV^[10].

Principio di minima azione

L'equazione KdV

${\displaystyle \partial _{t}\phi -6\phi \,\partial _{x}\phi +\partial _{x}^{3}\phi =0,\,}$

è l'equazione di Eulero–Lagrange derivata dalla densità di Lagrangiana, ${\displaystyle {\mathcal {L}}\,}$

${\displaystyle {\mathcal {L}}={\frac {1}{2}}\partial _{x}\psi \,\partial _{t}\psi +\left(\partial _{x}\psi \right)^{3}-{\frac {1}{2}}\left(\partial _{x}^{2}\psi \right)^{2}\,}$

in cui ${\displaystyle \phi }$ è definita come

${\displaystyle \phi ={\frac {\partial \psi }{\partial x}}=\partial _{x}\psi .\,}$

Dimostrazione

Poiché la lagrangiana contiene le derivate seconde, l'equazione di Eulero-Lagrange per il campo si scrive

${\displaystyle \partial _{\mu \mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu \mu }\psi )}}\right)-\partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)+{\frac {\partial {\mathcal {L}}}{\partial \psi }}=0}$

dove ${\displaystyle \partial }$ è una derivata rispetto alla componente ${\displaystyle \mu }$.

Scrivendo per esteso la precedente equazione si ottiene

${\displaystyle \partial _{tt}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{tt}\psi )}}\right)+\partial _{xx}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{xx}\psi )}}\right)-\partial _{t}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{t}\psi )}}\right)-\partial _{x}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{x}\psi )}}\right)+{\frac {\partial {\mathcal {L}}}{\partial \psi }}=0}$

e, sostituendo l'espressione della lagrangiana in ciascun termine della relazione,

${\displaystyle \partial _{tt}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{tt}\psi )}}\right)=0\,}$

${\displaystyle \partial _{xx}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{xx}\psi )}}\right)=\partial _{xx}\left(-\partial _{xx}\psi \right)\,}$

${\displaystyle \partial _{t}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{t}\psi )}}\right)=\partial _{t}\left({\frac {1}{2}}\partial _{x}\psi \right)\,}$

${\displaystyle \partial _{x}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{x}\psi )}}\right)=\partial _{x}\left({\frac {1}{2}}\partial _{t}\psi +3(\partial _{x}\psi )^{2}\right)\,}$

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial \psi }}=0\,}$

Ora, ricordando che si è definito ${\displaystyle \phi =\partial _{x}\psi \,}$,

${\displaystyle \partial _{xx}\left(-\partial _{xx}\psi \right)=-\partial _{xxx}\phi \,}$

${\displaystyle \partial _{t}\left({\frac {1}{2}}\partial _{x}\psi \right)={\frac {1}{2}}\partial _{t}\phi \,}$

${\displaystyle \partial _{x}\left({\frac {1}{2}}\partial _{t}\psi +3(\partial _{x}\psi )^{2}\right)={\frac {1}{2}}\partial _{t}\phi +3\partial _{x}(\phi )^{2}={\frac {1}{2}}\partial _{t}\phi +6\phi \partial _{x}\phi \,}$

Sostituendo nuovamente nell'equazione di Eulero-Lagrange si ottiene

${\displaystyle \left(-\partial _{xxx}\phi \right)-\left({\frac {1}{2}}\partial _{t}\phi \right)-\left({\frac {1}{2}}\partial _{t}\phi +6\phi \partial _{x}\phi \right)=0,\,}$

che corrisponde esattamente alla KdV

${\displaystyle \partial _{t}\phi +6\phi \,\partial _{x}\phi +\partial _{x}^{3}\phi =0}$

Asintoti

Si può mostrare che ogni soluzione liscia che decada abbastanza velocemente si divide sempre in una sopvrapposizione finita di solitoni che si muovono verso destra più una parte dispersiva che decade velocemente che si muove verso sinistra. Questo fenomeno è stato osservato per la prima volta da Zabuski e Kruskal nel 1965^[11][12].

Note

1. Boussinesq.
2. Korteweg-de Vries.
3. O. Darrigol, Worlds of Flow: A History of Hydrodynamics from the Bernoullis to Prandtl, Oxford University Press, 2005, p. 84, ISBN 978-0-19-856843-8.
4. N.J. Zabusky and M. D. Kruskal, Phy. Rev. Lett., 15, 240 (1965)
5. Cfr. Alan C. Newell, Solitons in mathematics and physics, SIAM, 1985, ISBN 0-89871-196-7., p. 6. e Lax (1968), senza il fattore 6.
6. Vladimir Igorevič Arnold, Metodi matematici della meccanica classica, Roma, Editori Riuniti University Press, 2010, p. 471.
7. Alexander F. Vakakis, Normal Modes and Localization in Nonlinear Systems, Springer, 31 gennaio 2002, pp. 105–108, ISBN 978-0-7923-7010-9. URL consultato il 27 ottobre 2012.
8. Miura-Gardner-Kruskal.
9. Dingemans, p. 733.
10. Lax.
11. Zabusky-Kruskal.
12. Grunert-Teschl.

Bibliografia

• J. Boussinesq, Essai sur la theorie des eaux courantes, collana Memoires presentes par divers savants ` l’Acad. des Sci. Inst. Nat. France, XXIII, 1877, pp. 1–680.
• E.M. de Jager, On the origin of the Korteweg–de Vries equation, 2006. arΧiv:math.HO/0202661
• M.W. Dingemans, Water wave propagation over uneven bottoms, collana Advanced Series on Ocean Engineering, vol. 13, World Scientific, Singapore, 1997, ISBN 981-02-0427-2., 2 Parts, 967 pages
• P. G. Drazin, Solitons, collana London Mathematical Society Lecture Note Series, vol. 85, Cambridge, Cambridge University Press, 1983, pp. viii+136, ISBN 0-521-27422-2.
• Katrin Grunert e Gerald Teschl, Long-Time Asymptotics for the Korteweg-de Vries Equation via Nonlinear Steepest Descent, in Math. Phys. Anal. Geom., vol. 12, n. 3, 2009, pp. 287–324, Bibcode:2009MPAG...12..287G, DOI:10.1007/s11040-009-9062-2, arXiv:0807.5041.
• Thomas Kappeler e Jürgen Pöschel, KdV & KAM, collana Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 45, Berlin, New York, Springer-Verlag, 2003, ISBN 978-3-540-02234-3.
• D. J. Korteweg e G. de Vries, On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationary Waves, in Philosophical Magazine, vol. 39, n. 240, 1895, pp. 422–443, DOI:10.1080/14786449508620739.
• P. Lax, Integrals of nonlinear equations of evolution and solitary waves, in Comm. Pure Applied Math., vol. 21, n. 5, 1968, pp. 467–490, DOI:10.1002/cpa.3160210503.
• John W. Miles, The Korteweg–De Vries equation: A historical essay, in Journal of Fluid Mechanics, vol. 106, 1981, pp. 131–147, Bibcode:1981JFM...106..131M, DOI:10.1017/S0022112081001559.
• Robert M. Miura, Clifford S. Gardner e Martin D. Kruskal, Korteweg–de Vries equation and generalizations. II. Existence of conservation laws and constants of motion, in J. Mathematical Phys., vol. 9, n. 8, 1968, pp. 1204–1209, Bibcode:1968JMP.....9.1204M, DOI:10.1063/1.1664701.
• N. J. Zabusky e M. D. Kruskal, Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States, in Phys. Rev. Lett., vol. 15, n. 6, 1965, pp. 240–243, Bibcode:1965PhRvL..15..240Z, DOI:10.1103/PhysRevLett.15.240.

Voci correlate

• Onda marina
• Solitone
• Onda cnoidale
• Numero di Ursell
• Approssimazione di Boussinesq (onde marine)
• Problema di Fermi-Pasta-Ulam-Tsingou

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su equazione di Korteweg-de Vries

Collegamenti esterni

• (EN) Eric W. Weisstein, Equazione di Korteweg-de Vries, su MathWorld, Wolfram Research.
• (EN) Equazione di Korteweg-de Vries, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• Korteweg–de Vries equation da EqWorld: The World of Mathematical Equations.
• Korteweg–de Vries equation Archiviato il 3 marzo 2016 in Internet Archive. da NEQwiki, the nonlinear equations encyclopedia.
• Cylindrical Korteweg–de Vries equation da EqWorld: The World of Mathematical Equations.
• Modified Korteweg–de Vries equation da EqWorld: The World of Mathematical Equations.
• Modified Korteweg–de Vries equation Archiviato il 3 marzo 2016 in Internet Archive. da NEQwiki, the nonlinear equations encyclopedia.
• Derivation sulla KdV in un canale stretto
• Tre solitoni nella KdV
• Tre solitoni instabili nella KdVThree –
• Discussione di aspetti matematici della KdV Dispersive PDE Wiki.
• Solitons from the Korteweg–de Vries Equation S. M. Blinder, The Wolfram Demonstrations Project.
• Solitons & Nonlinear Wave Equations, su lie.math.brocku.ca. URL consultato il 3 novembre 2015 (archiviato dall'url originale il 2 dicembre 2008).

Portale Fisica

Portale Matematica