Loading AI tools
proiezione equivalente Da Wikipedia, l'enciclopedia libera
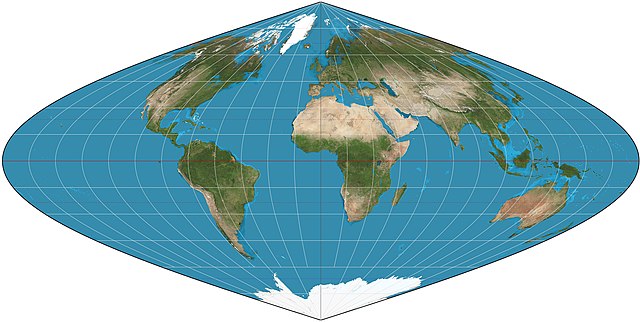
La proiezione sinusoidale o di Sanson–Flamsteed è una proiezione equivalente (cioè in cui il modulo di deformazione superficiale è unitario e le aree si conservano), la quale rappresenta porzioni di territorio compresi tra due paralleli e due meridiani tramite particolari quadrilateri: le trasformate dei paralleli sono delle rette mentre le trasformate dei meridiani sono degli elementi curvilinei.


Jean Cossin della scuola cartografica di Dieppe fu uno dei primi cartografi ad usare questa tecnica, in una carta del 1570. Fu successivamente ripresa da Nicolas Sanson e John Flamsteed. La proiezione sinusoidale, spesso detta di Sanson-Flamsteed, fu adottata per la prima edizione della Carta d'Italia alla scala 1:100.000 (1875) e l'Istituto Geografico Militare ha continuato ad utilizzarla fino al 1948, quando le fu preferita la proiezione di Gauss-Boaga[1].
La proiezione è definita da:
dove è la latitudine, è la longitudine, e è il meridiano centrale.[2]
La scala nord-sud è la stessa in ogni luogo rispetto al meridiano centrale, e quella est-ovest è similare in tutta la mappa; di conseguenza, sulla mappa, come nella realtà, la lunghezza di ogni parallelo è proporzionale al coseno della latitudine, così la forma della mappa di tutta la terra è l'area tra due curve coseniche simmetriche ruotate. La vera distanza tra due punti sullo stesso meridiano corrisponde alla distanza sulla carta tra le due linee parallele, che è minore della distanza tra i due punti sulla mappa. Non si hanno distorsioni sul meridiano centrale o equatore.

Proiezioni simili che avvolgono la parte est e ovest della proiezione sinusoidale attorno al polo nord sono le Werner e le intermedie Bonne e Bottomley.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.