La compressione indica nella meccanica uno degli sforzi elementari monoassiali normali alla superficie di riferimento al quale può essere sottoposto un corpo (insieme alla trazione, la flessione, il taglio e la torsione); si misura in MPa.

Descrizione
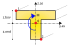
In una generica sezione di una trave soggetta a compressione semplice la tensione media si calcola con la relazione , in cui:
- Fn è la forza normale (N) parallela e negativa in modulo rispetto alla direzione esterna della superficie corpo a cui è applicata.
- A è l'area della sezione trasversale della trave (m2).
Il principio di resistenza a rottura per compressione fu illustrato da Galileo Galilei nel trattato Due nuove scienze del 1638 (giornata 1 - paragrafi iniziali). Dopo le sperimentazioni del Seicento e Settecento, la teoria tecnica e le formule della resistenza a compressione furono definite dall'ingegnere francese Claude-Louis Navier nel trattato Resumè des lecons del 1826 (Libro I - capitolo I compression) e perfezionate da De Saint-Venant nella seconda metà dell'Ottocento.
Le formule ricavate per il calcolo della sollecitazione a trazione si applicano identicamente a corpi compressi, purché questi non siano lunghi in confronto alle dimensioni della sezione trasversale (elementi tozzi). Se un solido cilindrico rettilineo molto lungo (elemento snello) è soggetto a una forza di compressione gradatamente crescente, raggiunto un certo valore del carico, detto carico critico Euleriano, esso s'inflette indefinitamente nel piano di minor rigidezza.
In questo caso il carico di collasso dipende anche dagli effetti geometrici del secondo ordine o non linearità geometrica (instabilità dell'equilibrio). Nella realtà è raro che si possa realizzare la compressione perfettamente centrata. Infatti gli errori esecutivi sono fattori che producono come risultato la presenza di un'eccentricità del carico e quindi la presenza di una sollecitazione di flessione che va a sommarsi allo sforzo normale. Si ha così la cosiddetta pressoflessione.
Voci correlate
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.