Բազմություն

Բազմություն, իրարից տարբեր օբյեկտների որոշակի հավաքածու, որն իր հերթին դիտարկվում է որպես օբյեկտ։ Բազմության մեջ օբյեկտների դասավորությունը նշանակություն չունի։ Բազմությունները կարող են նշվել ձևավոր փակագծերում՝ թվարկելով բազմության տարրերը։ Օրինակ՝ 2, 4, և 6 տարբեր օբյեկտներ են, երբ դրանք դիտարկվում են առանձին-առանձին, երբ դրանք դիտարկվում են որպես համախմբություն կամ հավաքածու, ապա այն երեք տարրերից բաղկացած պարզ բազմություն է {2, 4, 6}, որը կարող է ներկայացվել նաև {2, 6, 4}, {4, 2, 6}, {4, 6, 2}, {6, 2, 4} կամ {6, 4, 2}^[1] տեսքով։ Բազմությունները կարող են նաև նշանակվել լատինատառ մեծատառերով՝ ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$.^[2][3]

Բազմանկյունների բազմություն Էյլերի դիագրամի վրա

Բազմությունները մաթեմատիկայի ամենաֆունդամենտալ հասկացություններից են^[4]։ Զարգանալով 19-րդ դարի վերջում^[5], բազմությունների տեսությունը այժմ մաթեմատիկայի անբաժան մասն է։ Մաթեմատիկական կրթության մեջ, տարրական թեմաները այնպիսիք, ինչպիսին Վեն դիագրամներն են, ուսուցանվում են դպրոցական տարիքում, մինչդեռ ավելի բարձրակարգ հասկացությունները ուսուցանվում են որպես համալսարանական աստիճանի մաս։

Ծագումնաբանություն

Գերմաներեն Menge բառը, որ հայերենով թարգմանվում «բազմություն» կամ հավաքածու, հորինել է Բեռնարդ Բոլցանոն և հիշատակել իր Անվերջության պարադոքս աշխատության մեջ^[6][7][8]։

Սահմանում

Հատված Գեորգ Կանտորի բնօրինակ սահմանման՝ թարգմանությամբ: «Menge» գերմաներեն բառը «set»-ը այստեղ թարգմանվում է «հավաքածու» բառով

Բազմությունը, դա մեր ընկալման (Anschauung) և մեր մտքի մի շարք որոշակի, օբյեկտների խումբ է, որոնք կոչվում են հավաքածուի տարրեր։ ^[9][10] Օբյեկտները, որ միանալով բազմություն են կազմում (նաև հայտնի որպես բազմության տարրեր կամ անդամներ)^[11], կարող են լինել ամեն ինչ՝ թվեր, մարդիկ, այբուբենի տառեր, այլ բազմություններ և այլն^[12]։ Բազմությունների տեսության հիմնադիրնեից մեկը՝ Գեորգ Կանտորը իր Beiträge zur Begründung der transfiniten Mengenlehre սկզբում բազմության հետևյալ սահմանումն է տվել^[13]։

Բազմությունները սովորաբար նշանակվում են մեծատառերով^[2][12][14]։ A և B բազմությունները հավասար են այն և միայն այն ժամանակ, երբ ճշգրիտ միևնույն տարրերից են կազմված^[15]։

Տեխնիկական պատճառներից ելնելով, Կանտորի սահմանումը չեղարկվեց որպես ոչ ադեկվատ, այսօր, առավել ճշգրտություն պահանջող կոնտեքստում օգտագործվում է բազմությունների աքսիոմատիկ տեսությունը, որտեղ բազմության գաղափարըն ընդունվում է որպես պարզագույն հասկացություն, իսկ դրա հատկությունները սահմանվում են որպես աքսիոմների հավաքածու^[16]։ Ամենահիմնական հատկություններն են՝ բազմությունն ունի տարրեր և երկու բամություն համարժեք են, այն և միայն այն դեպքում, երբ մեկի յուրաքանչյուր տարր նաև երկրորդի տարր է^[17]։

Բազմության նշում

Բազմության անդամների նկարագրման երկու տարածված եղանակ գոյություն ունի․ Ռոսթերի նշանակում և բազմության կառուցման նշանակում^[18][19]։ Սրանք համապատասխանաբար բազմությունների նկարագրման քստենսիոն և ինտենսիոն սահմանումների օրինակներ են^[20]։

Ռոսթերի նշանակում

Ռոսթերի նշանակումը (կամ թվարկումով նշանակումը) դա բազմության յուրաքանչյուր անդամի թվարկման մեթոդ է^[18][21][22]։ Ավելի ստույգ, ռոսթեր նշանակման մեջ (ընդարձակ և բովանդակային նկարագրման օրինակ)^[20], բազմությունը ներկայացվում է ձևավոր փակագծերում անդամների թվարկմամբ․

A = {4, 2, 1, 3}

B = {կապույտ, սպիտակ, կարմիր}։

Մեծաթիվ տարրերով բազմությունների համար, անդամների թվարկումը կարելի է կրճատել^[23][24]։ Օրինակ, առաջին հազար դրական թվերի բազմությունը կարելի է ներկայացնել այսպես․

{1, 2, 3, ..., 1000},

որտեղ («...») - ը ցույց է տալիս, որ ցուցակը շարունակվում է ըստ ցուցադրված օրինաչափության^[23]։

Ռոսթերի նշանակման մեջ, անդամի կրկնություննը բազմությունը չի փոխում, օրինակ {11, 6, 6} և {11, 6} բազմությունները նույնն են^[25]։} Ավելին, բազմության տարրերի թվարկման կարգը կարևոր չէ (ի տարբերություն հաջորդականության կամ կորտեժ, ուստի {6, 11} միևնույն հավաքածուն է^[3][25]։

Բազմություն կառուցողի ներկայացում

Այս ներկայացման մեջ բազմությունը որոշվում էորպես ընտրություն ավելի մեծ բազմությունից, որ սահմանվում է անդամները ներառող պայմանով^[26][27]։ Օրինակ, F բազմությունը կարող է նկարագրվել հետևյալ կերպ․

${\displaystyle F=\{n\mid n{\text{ դրական ամբողջ թիվ է, և }}0\leq n\leq 19\}.}$

Այս ներկայացման մեջ, ուղղահայաց գիծը («|») նշանակում է «այնպիսին ինչպես», և նկարագրությունը կարող է մեկնաբանվել որպես «F-ը n այն բոլոր դրական ամբողջ թվերի բազմությունն է, որոնք ընկած են 0 ից 19 միջակայքում, ներառյալ 19-ը»։ Երբեմն ուղղահայաց գծի փոխարեն օգտագործվում է վերջակետի («:») նշանը^[28]։

Բազմություն կառուցողի գրառումը բովանդակային սահմանման օրինակ է^[20]։

Բազմության ներկայացման այլ եղանակներ

Բազմության ներկայացման այլ եղանակը սեմանտիկ նկարագրության կիրառումն է․^[29]

A -ն բազմություն է, որի անդամները առաջին չորս դրական ամբողջ թվերն են։

B -ն Ֆրանսիայի դրոշի գույների բազմությունն է։

Սա բովանդակային նկարագրության այլ օրինակ է^[20]։

Անդամակցություն

Հիմնական հոդված՝ Տարր (մաթեմատիկա)

Եթե B-ն բազմություն է և x-ը B-ի օբյեկտներից մեկն է, դա գրառվում է այսպես x ∈ B և կարդացվում՝ "x-ը B-ի տարր է", ինչպես "x-ը պատկանում է B-ին", կամ "x-ը B-ի մեջ է"^[17]։ Եթե y-ը B-ի անդամ չէ, ապա դա գրառվում է այսպես y ∉ B, կարդացվում «y-ը B-ի տարր չի», կամ «y -ը B-ում չէ»^[2][30][31]։

Օրինակ, A = {1, 2, 3, 4}, B = {կապույտ, սպիտակ, կարմիր}, և F = {n | n դրական ամբողջ թիվ է, և 0 ≤ n ≤ 19},

4 ∈ A և 12 ∈ F; և

20 ∉ F կանաչը ∉ B.

Ենթաբազմություններ

Եթե A-ի յուրաքանչյուր տարր առկա է նաև B-ում, ապա A-ն B-ի ենթաբազմություն է, գրառվում է A ⊆ B (արտասանվում է՝ A -ն պարունակվում է B-ում)^[32]։ Սրան համարժեք գրառում է՝ B ⊇ A (արտանսանվում է՝ B -ն A-ի բազմություն է, B ներառում է իր մեջ A-ն, կամ B -ն պարունակում է իր մեջ A-ն^[2][33]։ ⊆ նշանով բազմությունների հարաբերությունը կոչվում է ներառում կամ պարունակություն։ Երկու բազմություն հավասար են, եթե նրանք մեկը մյուսին պարունակում են․ A ⊆ B և B ⊆ A համարժեք է A = B^[26]։

Եթե A-ն B-ի ենթաբազմություն է, սակայն հավասար չէ B-ին, ապա A-ն կոչվում է B-ի իսկական ենթաբազմություն, գրառվում է A ⊊ B, կամ պարզապես A ⊂ B^[32] , կամ B ⊋ A (B-ն A-ի իսկական բազմություն է, B ⊃ A)^[2]։

A ⊂ B և B ⊃ A արտահայտությունները տարբեր հեղինակների կողմից տարբեր կերպ են օգտագործվում, որոշ հեղինակներ դրանք օգտագործում են նկատի ունենալով նույնը ինչ որ A ⊆ B^[30][34] (համապատասխանաբար B ⊇ A), մինչդեռ մյուսներն օգտագործում են դրանք `նույն իմաստով, ինչ A ⊊ B^[32] (respectively B ⊋ A)։

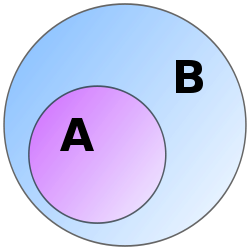
A-ն B-ի ենթաբազմությունն է

Օրինակներ։

• Բոլոր մարդկանց բազմությունը բոլոր կաթնասունների բազմության իսկական ենթաբազմությունն է։
• {1, 3} ⊆ {1, 2, 3, 4}։
• {1, 2, 3, 4} ⊆ {1, 2, 3, 4}։

Կա եզակի բազմություն՝ առանց անդամների^[35], կոչվում է դատարկ բազմություն (կամ զրո բազմություն), որը նշանակվում է ∅ սիմվոլով կամ {}^[2]։ Դատարկ բազմությունը յուրաքանչյուր բազմության ենթաբազմություն է^[36], և յուրաքանչյուր բազմություն ինքն իր ենթաբազմությունն է^[34]։

• ∅ ⊆ A։
• A ⊆ A։

Բաժիններ

S բազմության բաժինը նրա ոչ դատարկ ենթաբազմությունն է, այնպիսին, որ S-ի յուրաքանչյուր x տարր այդ ենթաբազմություններից ճիշտ մեկի տարր է։ Այսինքն, այդ ենթաբազմությունների ցանկացած զույգ չեն հատվում (այն իմաստով, որ բաժինների ցանկացած երկուսը ընդհանուր տարր չունեն, և բաժանման բոլոր ենթաբազմությունների գումարը S-ն է^[37][38]։

Հզոր բազմություններ

S բազմության բոլոր ենթաբազմությունների բազմությունը կոչվում է հզոր բազմություն^[26]։ Հզոր բազմությունը պարունակում է S-ը և դատարկ բազմությունը, քանի որ դրանք S-ի ենթաբազմություններ են։ Օրինակ՝ {1, 2, 3} բազմության հզոր բազմությունը հետևյալ {{1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, ∅} բազմությունն է։ S բազմության հզոր բազմությունը նշանակվում է P(S)^{[2][3][26][39]}։

n վերջավոր տարրերով բազմության հզոր բազմությունը ունի 2ⁿ տարրեր^[40]։ Օրինակ՝ {1, 2, 3} բազմությունն ունի երեք տարր և վերևում ներկայացված հզոր բազմությունն ունի 2³ = 8 տարր։

Անվերջ (հաշվելի, թե՝ անհաշվելի ) բազմության հզոր բազմությունն անհաշվելի է։ Ավելին, բազմության հզոր բազմությունը միշտ խիստ «մեծ» է սկզբնական բազմությունից, այն իմաստով, որ հնարավոր չէ S-ի յուրաքանչյուր տարր P (S) ճշգրիտ մեկ տարրի հետ զուգակցել^[41]։

Բազմության հզորություն

Հիմնական հոդված՝ Բազմության հզորություն

Դատարկ բազմության հզորությունը հավասար է զրոյի^[42]։

Որոշ բազմությունների հզորությունն անվերջ է։ Օրինակ, N բնական թվերի բազմությունն անվերջ է^[26]։ Որոշ անվերջ հզորություններ ավելի մեծ են մյուսներից։ Օրինակ, իրական թվերի բազմությունն ունի ավելի մեծ հզորություն, քան բնական թվերինը^[43]։ Այնուամենայնիվ կարելի է ցույց տալ, որ ուղիղ գծի հզորությունը (ուղղի կետերի քանակը) նույնն է ինչ որ այդ ուղղի ցանկացած հատվածի, ամբողջ հարթության և նույնիսկ ցանկացած վերջավոր Էվկլիդյան տարածության^[44]։

Հատուկ բազմություններ

ℕ բնական թվերը ℤ ամբողջ թվերի մաս են կազմում, որոնք էլ ℚ ռացիոնալ թվերի մաս են կազմում, սրանք էլ ℝ իրական թվերի, որոնք և ℂ կոմպլեքս թվերի մաաս են կազմում։

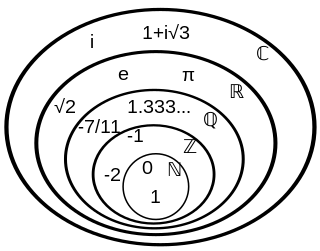
Մի շարք բազմություններ, կամ բազմությունների տեսակներ, որոնք մաթեմատիկական մեծ կարևորություն ունեն և այնպիսի հաճախականությամբ են հիշատակվում, որ իրենց իդենտիֆիկացմանհամար ձեռք են բերել հատուկ անուններ և նշանակումներ։Այդպիսի բազմություններից է դատարկ բազմությունը՝{ } կամ ∅.^[2][36] Ճիշտ մեկ x տարրով բազմությունը միավոր բազմություն է, կամ սինգլթոն {x}^[15], այն տարբերվում է x-ից^[45]։

Այս բազմություններից շատերը ներկայացվում են թավատառ (P) կամ կիսաթավատառ (ℙ)^[46]։ These include^[2]:

• P կամ ℙ-ով է նշանակվում պարզ թվերի բազմությունը․ P = {2, 3, 5, 7, 11, 13, 17, ...}.^[47]
• N կամ ℕ-ով է նշանակվում բնական թվերի բազմությունը․ N = {0, 1, 2, 3, ...} (sometimes defined excluding 0).^[46]
• Z կամ ℤ-ով է նշանակվում ամբողջ թվերի բազմությունը (դրական, բացասական և զրո)։ Z = {..., −2, −1, 0, 1, 2, ...}.^[46]
• Q կամ ℚ-ով է նշանակվում ռացիոնալ թվերի բազմությունը (բոլոր կանոնավոր և անկանոն կոտորակների բազմությունը)․ Q = {a/b | a, b ∈ Z, b ≠ 0}. Օրինակ, 1/4 ∈ Q և 11/6 ∈ Q. Բոլոր ամբողջ թվերը այս բազմության մեջ են, քանի որ յուրաքանչյուր a թիվ կարելի է ներկայացնել կոտորակի տեսքով՝ a/1 (Z ⊊ Q)^[46]։
• R կամ ℝ-ով է նշանակվում բոլոր իրական թվերի բազմությունը։ Այս բազմությունը ներառում է բոլոր ռացիոնալ և իռացիոնալ թվերը (այսինքն հանրահաշվական թվերը չեն կարող ներկայացվել կոտորակի տեսքով, ինչպես √2, ինչպես նաև տրանսցենդենտ թվերը, ինչպիսին են π, e)^[46]։
• C or ℂ-ով է նշանակվում բոլոր կոմպլեքս թվերի բազմությունը․ C = {a + bi | a, b ∈ R}. Օրինակ, 1 + 2i ∈ C.^[46]
• H կամ ℍ-ով է նշանակվում բոլոր քվատերնոների բազմությունը․ H = {a + bi + cj + dk | a, b, c, d ∈ R}. Օրինակ, 1 + i + 2j − k ∈ H^[48]։

Վերոնշյալ բոլոր բազմություններն անվերջ են և յուրաքանչյուրը իր ստորևի իսկական ենթաբազմություն է։ Պարզ թվերը Թվերի տեսությունից և հարակից ոլորտներից դուրս ավելի հազվադեպ են օգտագործվում։

Դրական կամ բացասական բազմությունները երբեմն նշվում են վերատառ համապատասխանաբար դրական և բացասական նշաններով։ Օրինակ, ℚ⁺ ներկայացնում է դրական ռացիոնալ թվերի բազմությունը։

Հիմնական գործողություններ

Գոյություն ունեն մի քանի հիմնարար գործողություններ տված բազմություններից նոր բազմություններ կառուցելու համար։

Միավորումներ

A և B-ի միավորումը նշանակվում է A ∪ B

Հիմնական հոդված՝ Միավորում (Բազմությունների տեսություն)

Երկու բազմություն կարելի գումարել միմյանց։ A և B-ն կարելի է միավորումը՝ A ∪ B^[2], այն բազմություն է, որի անդամները բոլոր այն օբյեկտներն են, որ կամ A-ի կամ B-ի անդամներ են։

Օրինակներ։

• {1, 2} ∪ {1, 2} = {1, 2}.
• {1, 2} ∪ {2, 3} = {1, 2, 3}.
• {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}

Միավորման մի քանի հիմնական հատկություններ․

• A ∪ B = B ∪ A.
• A ∪ (B ∪ C) = (A ∪ B) ∪ C.
• A ⊆ (A ∪ B).
• A ∪ A = A.
• A ∪ ∅ = A.
• A ⊆ B այն և միայն այն դեպքում, երբ A ∪ B = B.

Հատում

Հիմնական հոդված՝ Հատում (Բազմությունների տեսություն)

Նոր բազմություն կարելի է կառուցել նաև տարրերից, որոնք ընդհանուր են երկու բազմությունների համար։ A և B բազմությունների հատումը նշանակվում է A ∩ B,^[2] և իրենից ներկայացնում է այն օբյեկտները, որոնք միաժամանակ A և B բազմությունների անդամ են։ Եթե A ∩ B = ∅, ապա A և B բազմությունները չեն հատվում։

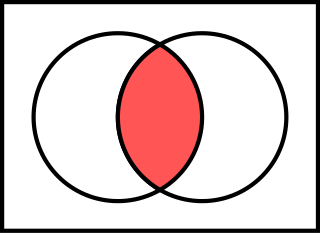
A and B բազմությունների հատումը նշանակվում է A ∩ B.

Օրինակներ։

• {1, 2} ∩ {1, 2} = {1, 2}.
• {1, 2} ∩ {2, 3} = {2}.
• {1, 2} ∩ {3, 4} = ∅.

Հատումների մի քանի հիմնական հատկություններ

• A ∩ B = B ∩ A.
• A ∩ (B ∩ C) = (A ∩ B) ∩ C.
• A ∩ B ⊆ A.
• A ∩ A = A.
• A ∩ ∅ = ∅.
• A ⊆ B այն և միայն այն դեպքում, երբ A ∩ B = A.

Լրացումներ

Հիմնական հոդված՝ Լրացում (Բազմությունների տեսություն)

Երկու բազմություններ կարող են նաև մեկը մյուսից "հանել"։ The relative complement of B-ի հարաբերական լրացումը A-ում (նաև անվանվում է A և B-ի բազմությունների տարբերություն), գրառվում է A \ B (կամ A − B)^[2], դա is the set of all elements that are members of A,-ի բոլոր այն տարրերի բազմությունն է, որոնք B-ի անդամ չեն։ Թույլատրելի է նաև բազմությունից հանել անդամներ, որոնք տվյալ բազմության անդամ չեն, այնպես որ կանաչ տարրը հանել {1, 2, 3}բազմությունից, այս կերպ վարվելը չի ազդի բազմության տարրերի վրա։ Որոշակի պայմաններում քննարկվող բոլոր բազմությունները ենթադրվում են որպես U մաթեմատիկական տարածության ենթաբազմություններ. Այդ դեպքում U \ A-ը կոչվում է A-ի բացարձակ լրացում կամ պարզապես լրացումև նշանակվում որպես A′ կամ A^c[2]․

• A′ = U \ A

Օրինակներ։

• {1, 2} \ {1, 2} = ∅.
• {1, 2, 3, 4} \ {1, 3} = {2, 4}.
• Եթե U-ն ամբողջ թվերի բազմությունն է, E-ն զույգ թվերի և O-ի, ապա կենտ թվերի բազմությունը կլինի U \ E = E′ = O.

Լրացման մի քանի հիմնական հատկություններն են՝

• A \ B ≠ B \ A, երբ A ≠ B։
• A ∪ A′ = U.
• A ∩ A′ = ∅.
• (A′)′ = A.
• ∅ \ A = ∅.
• A \ ∅ = A.
• A \ A = ∅.
• A \ U = ∅.
• A \ A′ = A և A′ \ A = A′.
• U′ = ∅ և ∅′ = U.
• A \ B = A ∩ B′.
• Եթե A ⊆ B, ապա A \ B = ∅.

A, B բազմությունների համար սահմանված լրացման ընդլայնումը սիմետրիկ տարբերությունն է և գրառվում է․

${\displaystyle A\,\Delta \,B=(A\setminus B)\cup (B\setminus A).}$

Օրինակ, {7, 8, 9, 10} և {9, 10, 11, 12} բազմությունների սիմետրիկ տարբերությունը {7, 8, 11, 12} բազմությունն է։

Դեկարտյան արտադրյալ

Նոր բազմություն կարելի է կառուցել միավորելով մի բազմության յուրաքանչյուր տարր, միավորելով մեկ այլ բազմության յուրաքանչյուր տարրի հետ։ Երկու A և B բազմությունների Դեկարտյան արտադրյալ A × B նշանակմամբ^[2], դա բոլոր (a, b) կարգավորված զույգերի բազմությունն է, այնպես որ a A-ի անդամ է և b-ն B-ի անդամ է։

Օրինակներ․

• {1, 2} × {կարմիր, սպիտակ, կանաչ} = {(1, կարմիր), (1, սպիտակ), (1, կանաչ), (2, կարմիր), (2, սպիտակ), (2, կանաչ)}։
• {1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.
• {a, b, c} × {d, e, f} = {(a, d), (a, e), (a, f), (b, d), (b, e), (b, f), (c, d), (c, e), (c, f)}.

Դեկարտյան արտադրյալի որոշ հիմնական հատկություններ՝

• A × ∅ = ∅.
• A × (B ∪ C) = (A × B) ∪ (A × C).
• (A ∪ B) × C = (A × C) ∪ (B × C).

Թող A և B-ն վերջավոր բազմություններ են, ապա դեկարտյան արտադրյալի հզորությունը հավասար է այդ բազմությունների հզորությունների արտադրյալը․

• | A × B | = | B × A | = | A | × | B |.

Կիրառություններ

Բազմությունների տեսությունը դիտարկվում է որպես հիմք, որից բոլոր մաթեմատիկայի մոլոր ճյուղերը կարելի է դուրս բերել։ Օրինակ՝ աբստրակտ հանրահաշվի հանրահաշվական կառուցվածքները, ինչպիսիք են խմբերը, դաշտերը, օղակները բազմություններ են մեկ կամ մի քանի գործողություններ կատարելու ժամանակ։

Բազմությունների տեսության գլխավոր կիրառություններից մեկը հարաբերությունների կառուցումն է։ A տիրույթի հարաբերությունը B համատիրույթի հետ A × B' դեկարտյան արտադրյալի ենթաբազմություն է։

Առընչություններ բազմությունների միջև

Էյլերի դիագրամ ${\displaystyle A\subset B}$համար

${\displaystyle A}$ և ${\displaystyle B}$ երկու բազմությունները կարող են միմյանց հետ տարբեր առընչություն ունենալ

• ${\displaystyle A}$ ընդգրկում ${\displaystyle B}$, եթե ${\displaystyle A}$-ի յուրաքանչյուր անդամը պատկանում է նաև ${\displaystyle B}$ բազմությանը։

  ${\displaystyle A\subseteq B\Leftrightarrow \forall a\in A\colon a\in B}$

• ${\displaystyle A}$ ընդգրկում է ${\displaystyle B}$, եթե ${\displaystyle B}$ պատկանում է ${\displaystyle A}$:

  ${\displaystyle A\supseteq B\Leftrightarrow B\subseteq A}$

• ${\displaystyle A}$ հավասար է ${\displaystyle B}$, եթե ${\displaystyle A}$ և ${\displaystyle B}$ ընդգրկում են մեկը մյուսին։

  ${\displaystyle A=B\Leftrightarrow (A\subseteq B)\land (B\subseteq A)}$

  • Ցանկացած բազմության համար ${\displaystyle A=A}$
  • Եթե ${\displaystyle A=B}$, ապա ${\displaystyle B=A}$
  • Եթե ${\displaystyle A=B}$, ${\displaystyle B=C}$, ապա ${\displaystyle A=C}$.
• ${\displaystyle A}$ խստորեն պատկանում է ${\displaystyle B}$, եթե ${\displaystyle A}$պատկանում է ${\displaystyle B}$, բայց նրան հավասար չէ։

  ${\displaystyle A\subset B\Leftrightarrow (A\subseteq B)\land (A\neq B)}$

• ${\displaystyle A}$ խստորեն պատկանում է ${\displaystyle B}$, եթե ${\displaystyle B}$ խստորեն պատկանում է ${\displaystyle A}$:

  ${\displaystyle A\supset B\Leftrightarrow B\subset A}$

• ${\displaystyle A}$ և ${\displaystyle B}$ չեն հատվում,եթե ընդհանուր անդամներ չունեն։

  ${\displaystyle A}$ և ${\displaystyle B}$ չեն հատվում ${\displaystyle \Leftrightarrow \forall a\in A\colon a\notin B}$

• ${\displaystyle A}$ և ${\displaystyle B}$ գտնվում են ընդհանուր վիճակում, եթե գոյություն ունի անդամ, որ պատկանում է միայն ${\displaystyle A}$ բազմությանը, անդամ, որ պատկանում է միայն ${\displaystyle B}$-ին և անդամ, որ պատկանում է երկուսին էլ։

  ${\displaystyle A}$ և ${\displaystyle B}$ գտնվում են ընդհանուր վիճակում ${\displaystyle \Leftrightarrow }$ ${\displaystyle \exists a,b,c\colon (a\in A)\land (a\notin B)\land (b\in B)\land (b\notin A)\land (c\in A)\land (c\in B)}$

Գործողություններ բազմությունների հետ

Վենի դիագրամ ${\displaystyle A\cap B}$համար

Վենի դիագրամ ${\displaystyle A\cup B}$համար

Վենի դիագրամ ${\displaystyle A\setminus B}$համար

Վենի դիագրամ ${\displaystyle A\triangle B}$համար

• հատում․

  ${\displaystyle A\cap B:=\{x\mid x\in A\land x\in B\}}$.

• միավորում․

  ${\displaystyle A\cup B:=\{x\mid x\in A\lor x\in B\}}$.

Եթե ${\displaystyle A}$ և ${\displaystyle B}$ բազմությունները չեն հատվում, ապա ${\displaystyle A\cap B=\varnothing }$. Նրանց միավորումը նշանակում են նաև հետյալ ձևով՝ ${\displaystyle A+B=A\cup B}$

• տարբերություն․

  ${\displaystyle A\setminus B:=A\cap {\overline {B}}=\{x\mid x\in A\land x\notin B\}}$.

• համաչափ տարբերություն․

  ${\displaystyle A\bigtriangleup B\equiv A\;\;\!\!{\dot {-}}\;\;\!\!B:=}$

  ${\displaystyle (A\cup B)\setminus (A\cap B)=A\cap {\overline {B}}+{\overline {A}}\cap B=}$

  ${\displaystyle =\{x\mid (x\in A\land x\notin B)\lor (x\notin A\land x\in B)\}}$.

• դեկարտյան կանմ ուղիղ արտադրյալ․

  ${\displaystyle A\times B=\{(a,\;b)\mid a\in A,\;b\in B\}}$.

Վենի դիագրամ ${\displaystyle (A\cap B)^{\complement }}$համար

Բազմության տարրեր կամ անդամներ կարող են լինել՝ թվեր, մարդիկ, այբուբենի տառեր, ուրիշ բազմություններ և այլն։ Բազմությունները պայմանականորեն նշանակվում են մեծատառերով։ A և B բազմությունները հավասար են այն և միայն այն դեպքում, երբ նրանք բաղկացած են ճիշտ նույն էլեմենտներից^[15]։

Ծանոթագրություններ

1. D. Van Dalen; H. C. Doets; H. De Swart (2014 թ․ մայիսի 9). Sets: Naïve, Axiomatic and Applied: A Basic Compendium with Exercises for Use in Set Theory for Non Logicians, Working and Teaching Mathematicians and Students. Elsevier Science. էջ 1. ISBN 978-1-4831-5039-0.
2. «Comprehensive List of Set Theory Symbols». Math Vault (ամերիկյան անգլերեն). 2020 թ․ ապրիլի 11. Վերցված է 2020 թ․ օգոստոսի 19-ին.
3. «Introduction to Sets». www.mathsisfun.com. Վերցված է 2020 թ․ օգոստոսի 19-ին.
4. Paul R. Halmos (2017 թ․ ապրիլի 19). Naive Set Theory. Courier Dover Publications. էջ 1. ISBN 978-0-486-81487-2.
5. José Ferreirós (2007 թ․ օգոստոսի 16). Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Birkhäuser Basel. ISBN 978-3-7643-8349-7.
6. Steve Russ (2004 թ․ դեկտեմբերի 9). The Mathematical Works of Bernard Bolzano. OUP Oxford. ISBN 978-0-19-151370-1.
7. William Ewald; William Bragg Ewald (1996). From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics. OUP Oxford. էջ 249. ISBN 978-0-19-850535-8.
8. Paul Rusnock; Jan Sebestík (2019 թ․ ապրիլի 25). Bernard Bolzano: His Life and Work. OUP Oxford. էջ 430. ISBN 978-0-19-255683-7.
9. P. K. Jain; Khalil Ahmad; Om P. Ahuja (1995). Functional Analysis. New Age International. էջ 1. ISBN 978-81-224-0801-0.
10. Samuel Goldberg (1986 թ․ հունվարի 1). Probability: An Introduction. Courier Corporation. էջ 2. ISBN 978-0-486-65252-8.
11. Thomas H.. Cormen; Thomas H Cormen; Charles E Leiserson; Ronald L Rivest; Clifford Stein (2001). Introduction To Algorithms. MIT Press. էջ 1070. ISBN 978-0-262-03293-3.
12. Halmos 1960, էջ. 1 harvnb error: no target: CITEREFHalmos1960 (help)
13. "Eine Menge, ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung und unseres Denkens – welche Elemente der Menge genannt werden – zu einem Ganzen."
14. Seymor Lipschutz; Marc Lipson (1997 թ․ հունիսի 22). Schaum's Outline of Discrete Mathematics. McGraw Hill Professional. էջ 1. ISBN 978-0-07-136841-4.
15. Stoll, Robert (1974). Sets, Logic and Axiomatic Theories. W. H. Freeman and Company. էջեր 5.
16. Jose Ferreiros (2001 թ․ նոյեմբերի 1). Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Springer Science & Business Media. ISBN 978-3-7643-5749-8.
17. Halmos 1960, էջ. 2 harvnb error: no target: CITEREFHalmos1960 (help)
18. Charles Roberts (2009 թ․ հունիսի 24). Introduction to Mathematical Proofs: A Transition. CRC Press. էջ 45. ISBN 978-1-4200-6956-3.
19. Ignacio Bello; Anton Kaul; Jack R. Britton (2013 թ․ հունվարի 29). Topics in Contemporary Mathematics. Cengage Learning. էջ 47. ISBN 1-133-10742-7.
20. Frank Ruda (2011 թ․ հոկտեմբերի 6). Hegel's Rabble: An Investigation into Hegel's Philosophy of Right. Bloomsbury Publishing. էջ 151. ISBN 978-1-4411-7413-0.
21. David Johnson; David B. Johnson; Thomas A. Mowry (June 2004). Finite Mathematics: Practical Applications (Docutech Version). W. H. Freeman. էջ 220. ISBN 978-0-7167-6297-3.
22. Susanna S. Epp (2010 թ․ օգոստոսի 4). Discrete Mathematics with Applications. Cengage Learning. էջ 13. ISBN 0-495-39132-8.
23. Alfred Basta; Stephan DeLong; Nadine Basta (2013 թ․ հունվարի 1). Mathematics for Information Technology. Cengage Learning. էջ 3. ISBN 1-285-60843-7.
24. Laura Bracken; Ed Miller (2013 թ․ փետրվարի 15). Elementary Algebra. Cengage Learning. էջ 36. ISBN 0-618-95134-2.
25. Stephen B. Maurer; Anthony Ralston (2005 թ․ հունվարի 21). Discrete Algorithmic Mathematics. CRC Press. էջ 11. ISBN 978-1-4398-6375-6.
26. John F. Lucas (1990). Introduction to Abstract Mathematics. Rowman & Littlefield. էջ 108. ISBN 978-0-912675-73-2.
27. Weisstein, Eric W. «Set». mathworld.wolfram.com (անգլերեն). Վերցված է 2020 թ․ օգոստոսի 19-ին.
28. Ralph C. Steinlage (1987). College Algebra. West Publishing Company. ISBN 978-0-314-29531-6.
29. Halmos 1960, էջ. 4 harvnb error: no target: CITEREFHalmos1960 (help)
30. Marek Capinski; Peter E. Kopp (2004). Measure, Integral and Probability. Springer Science & Business Media. էջ 2. ISBN 978-1-85233-781-0.
31. «Set Symbols». www.mathsisfun.com. Վերցված է 2020 թ․ օգոստոսի 19-ին.
32. Felix Hausdorff (2005). Set Theory. American Mathematical Soc. էջ 30. ISBN 978-0-8218-3835-8.
33. Peter Comninos (2010 թ․ ապրիլի 6). Mathematical and Computer Programming Techniques for Computer Graphics. Springer Science & Business Media. էջ 7. ISBN 978-1-84628-292-8.
34. Halmos 1960, էջ. 3 harvnb error: no target: CITEREFHalmos1960 (help)
35. K.T. Leung; Doris Lai-chue Chen (1992 թ․ հուլիսի 1). Elementary Set Theory, Part I/II. Hong Kong University Press. էջ 27. ISBN 978-962-209-026-2.
36. Halmos 1960, էջ. 8 harvnb error: no target: CITEREFHalmos1960 (help)
37. Toufik Mansour (2012 թ․ հուլիսի 27). Combinatorics of Set Partitions. CRC Press. ISBN 978-1-4398-6333-6.
38. Halmos 1960, էջ. 28 harvnb error: no target: CITEREFHalmos1960 (help)
39. Halmos 1960, էջ. 19 harvnb error: no target: CITEREFHalmos1960 (help)
40. Halmos 1960, էջ. 20 harvnb error: no target: CITEREFHalmos1960 (help)
41. Edward B. Burger; Michael Starbird (2004 թ․ օգոստոսի 18). The Heart of Mathematics: An invitation to effective thinking. Springer Science & Business Media. էջ 183. ISBN 978-1-931914-41-3.
42. Karl J. Smith (2008 թ․ հունվարի 7). Mathematics: Its Power and Utility. Cengage Learning. էջ 401. ISBN 0-495-38913-7.
43. John Stillwell (2013 թ․ հոկտեմբերի 16). The Real Numbers: An Introduction to Set Theory and Analysis. Springer Science & Business Media. ISBN 978-3-319-01577-4.
44. David Tall (2006 թ․ ապրիլի 11). Advanced Mathematical Thinking. Springer Science & Business Media. էջ 211. ISBN 978-0-306-47203-9.
45. Halmos 1960, Sect.2 harvnb error: no target: CITEREFHalmos1960 (help) Որպես անալոգիա, Հալմոսը նշում է, որ գլխարկ պարունակող տուփը նույնը չէ, ինչ գլխարկը։
46. George Tourlakis (2003 թ․ փետրվարի 13). Lectures in Logic and Set Theory: Volume 2, Set Theory. Cambridge University Press. էջ 137. ISBN 978-1-139-43943-5.
47. Abhijit Das (2016 թ․ ապրիլի 19). Computational Number Theory. CRC Press. էջ 2. ISBN 978-1-4822-0582-4.
48. D.L. Johnson (2012 թ․ դեկտեմբերի 6). Elements of Logic via Numbers and Sets. Springer Science & Business Media. էջ 165. ISBN 978-1-4471-0603-6.