Részcsoport
From Wikipedia, the free encyclopedia
Egy csoport részcsoportjai azok a nem üres részhalmazai, amik szintén zártak a csoport műveleteire, a szorzásra és az invertálásra nézve, és tartalmazzák az egységelemet. Ha a H csoport részcsoportja G-nek, akkor ennek jele . Minden csoportnak vannak részcsoportjai, részcsoport például az egységelemből álló egyelemű halmaz minden csoportban, és az egész csoport is részcsoportja önmagának. Részcsoportok metszete is részcsoport. Két részcsoport uniója akkor és csak akkor részcsoport, ha az egyik tartalmazza a másikat. A részcsoportok generálhatók. Egy csoport részcsoportjai hálót alkotnak a tartalmazásra, mint rendezésre, a halmazelméleti metszetre, mint metszetre, és a halmazelméleti unió általi generálásra, mint egyesítésre nézve.
Ekvivalens definíciók
Egy G csoport H nem üres halmazára nézve ekvivalensek:
- H tartalmazza az egységelemet, zárt a szorzásra és az invertálásra
Tulajdonságok
- Az egyelemű csoportnak egy részcsoportja van, az egyelemű csoport, vagyis önmaga. Az összes többi csoportnak legalább két részcsoportja van, az egyelemű és önmaga, amik nem esnek egybe. Ezek a triviális részcsoportok.
- Akárhány részcsoport metszete is részcsoport.
- Egy csoport részcsoportjai teljes hálót alkotnak, amiben az egyelemű részcsoport a nullelem, és az egész csoport az egységelem.
- A részcsoportnak lenni reláció antiszimmetrikus, tranzitív és reflexív.
- Lagrange tétele szerint a részcsoport mérete osztja a tartalmazó csoport méretét. Ebből következik, hogy a prímrendű csoportoknak csak a két triviális részcsoportja van.
Generálás
A részcsoportok generálhatók, azaz egy csoport minden részhalmaza generál egy csoportot. A generált részcsoport az a legkisebb részcsoport, ami a halmaz összes elemét tartalmazza. Belátható, hogy ez a csoport az egységelemből, a halmaz elemeiből és azok inverzeiből képzett véges hosszú szorzatokból (végtelen szorzathoz analízis kell) áll. Az E halmaz által generált csoport:
Az egy elem által generált csoportok ciklikus csoportok, és a generátorelem egész kitevős hatványaiból állnak. A ciklikus csoport mérete, vagyis rendje megegyezik generátoreleme rendjével.
Mellékosztályok
Egy H részcsoport bal oldali, illetve jobb oldali mellékosztályai a hH, illetve a Hh alakú halmazok, ahol h eleme H-nak. A bal és a jobb oldali mellékosztályok száma megegyezik; ez a részcsoport indexe. Minden mellékosztály mérete megegyezik a részcsoport rendjével. Az azonos oldali mellékosztályok diszjunktak. Ha a jobb és a bal oldali mellékosztályok megegyeznek, akkor a részcsoport normálosztó. Ez alapján bizonyítható Lagrange tétele, hogy a tartalmazó csoport rendje megegyezik a részcsoport rendjének és indexének szorzatával.
Példák
- nem részcsoportja -nak, mert más a művelet
- A szimmetrikus csoportban a páros permutációk részcsoportot alkotnak, az alternáló csoportot
Nyolcadrendű ciklikus csoport részcsoportjai
Jelölje a Z8 ciklikus csoportot , ahol a művelet a modulo 8 összeadás:
| + | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
| 2 | 2 | 4 | 6 | 0 | 3 | 5 | 7 | 1 |
| 4 | 4 | 6 | 0 | 2 | 5 | 7 | 1 | 3 |
| 6 | 6 | 0 | 2 | 4 | 7 | 1 | 3 | 5 |
| 1 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0 |
| 3 | 3 | 5 | 7 | 1 | 4 | 6 | 0 | 2 |
| 5 | 5 | 7 | 1 | 3 | 6 | 0 | 2 | 4 |
| 7 | 7 | 1 | 3 | 5 | 0 | 2 | 4 | 6 |
A nem triviális részcsoportok: J={0,4} és H={0,2,4,6}, ahol .
Az S4 szimmetrikus csoport részcsoportjai
Az S4 szimmetrikus csoport részcsoportként tartalmazza a triviális részcsoportokat, valamint az egységelem és a másodrendű elemek által alkotott csoportokat. Ezeket a továbbiakban nem tüntetjük fel.

12 elemű részcsoportok

8 elemű részcsoportok
 Részcsoportjai:    |  Részcsoportjai: 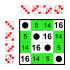  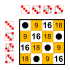 |  Részcsoportjai: 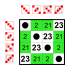  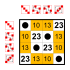 |
6 elemű részcsoportok
 Részcsoportjai:  |  Részcsoportjai:  |  Részcsoportjai:  |  Részcsoportjai:  |
4 elemű részcsoportok
 |  |  |  |
 |  |  |
3 elemű részcsoportok
 |  |  |
 |
További információk
Források
- Kiss Emil a részcsoportokról
- Kiss Emil a részcsoportok generálásáról
- Kurt Meyberg: Algebra - Teil 1. Hanser 1980, ISBN 3-446-13079-9
Wikiwand - on
Seamless Wikipedia browsing. On steroids.









