HU
All
Articles
Dictionary
Quotes
Map

Wikiwand ❤️ Wikipedia

PrivacyTerms
Bipoláris koordináta-rendszer

Bipoláris koordináta-rendszer

From Wikipedia, the free encyclopedia

Bipoláris koordináta-rendszer
DefinícióKoordinátavonalakKapcsolat a Descartes-koordinátákkalSkálázási tényezőkAz ortogonalitás bizonyításaAlkalmazásokKiterjesztések három dimenzióraJegyzetekForrásokFordítás

A bipoláris koordináta-rendszer egy kétdimenziós ortogonális koordináta-rendszer, ami az Apollóniusz-körökön alapul.[1] Megtévesztő lehet, hogy különböző szerzők más koordináta-rendszereket is bipolárisnak neveznek, mint a kétközepű bipoláris koordinátákat (ahol a két középpontól mért távolságok adják a koordinátákat), és a hasonló elven alapuló kétszögű koordinátákat.

Thumb
Bipoláris koordináta-rendszer. A σ-körök pirossal, a τ-körök kékkel ábrázolva. Fókuszok a ( − 1 ; 0 ) {\displaystyle (-1;0)} {\displaystyle (-1;0)} és az ( 1 ; 0 ) {\displaystyle (1;0)} {\displaystyle (1;0)} pontokban

A bipoláris szót használják olyan görbék leírására, melyeknek két fókuszpontjuk van, mint ellipszisek, hiperbolák és Cassini-oválisok. Azonban nem nevezik bipolárisnak az ezeken az alakzatokon alapuló koordináta-rendszereket, mint például az elliptikus koordinátákat.

Thumb
A bipoláris koordináták geometriai jelentése. A σ szöget a két fókusz és a P pont alkotja, míg τ a fókuszoktól mért távolságok arányának logaritmusa. A σ és τ konstansoknak megfelelő körök rendre pirossal, illetve kékkel ábrázolva, és derékszögben metszik egymást, amit magenta doboz jelöl

A rendszert két fókuszpont, F1 és F2 határozza meg. Egy P pont σ koordinátája megegyezik az F1 P F2 szöggel, míg a τ koordináta a fókuszoktól mért távolságok, d1 és d2 arányának természetes logaritmusa:

τ = ln ⁡ d 1 d 2 . {\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}.} {\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}.}

Ha felveszünk egy Descartes-féle koordinátarendszert úgy, hogy a két fókusz koordinátái (−a, 0) és (a, 0) legyenek, akkor a P pont koordinátái:

x = a   sh ⁡ τ ch ⁡ τ − cos ⁡ σ , y = a   sin ⁡ σ ch ⁡ τ − cos ⁡ σ . {\displaystyle x=a\ {\frac {\operatorname {sh} \tau }{\operatorname {ch} \tau -\cos \sigma }},\qquad y=a\ {\frac {\sin \sigma }{\operatorname {ch} \tau -\cos \sigma }}.} {\displaystyle x=a\ {\frac {\operatorname {sh} \tau }{\operatorname {ch} \tau -\cos \sigma }},\qquad y=a\ {\frac {\sin \sigma }{\operatorname {ch} \tau -\cos \sigma }}.}

τ értéke bármely valós szám lehet, míg a σ koordináta csak 2π periódus erejéig meghatározott, és többnyire -π és π között definiálják. Negatív értéket akkor vesz fel, ha a P pont az alsó félsíkon, tehát az F1F2 egyenes alatt van.

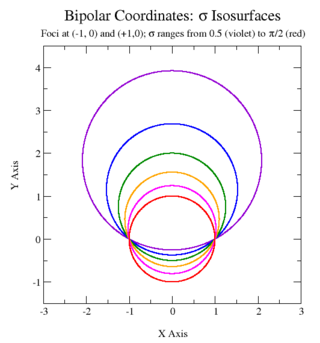
A konstans σ-nak megfelelő görbék nem koncentrikus körök:

x 2 + ( y − a ctg ⁡ σ ) 2 = a 2 sin 2 ⁡ σ {\displaystyle x^{2}+\left(y-a\operatorname {ctg} \sigma \right)^{2}={\frac {a^{2}}{\sin ^{2}\sigma }}} {\displaystyle x^{2}+\left(y-a\operatorname {ctg} \sigma \right)^{2}={\frac {a^{2}}{\sin ^{2}\sigma }}}

amelyek a fókuszokban metszik egymást. A konstans σ-jú körök középpontjai az y-tengelyre esnek. A pozitív σ-jú körök középpontja az x-tengely fölött található, míg a negatív σ-hoz tartozó körök középpontjai az x-tengely alá esnek. A |σ|- π/2 mennyiség csökkenésével a körök zsugorodnak, középpontjuk pedig a (0, 0) origóhoz közelít; melyet akkor ér el, ha |σ| = π/2. A Thalész-tétel szerint, ha egy háromszög két csúcsa átellenes egy körön, és a harmadik csúcsa is a körön helyezkedik el, akkor a háromszög derékszög.

A konstans τ-jú görbék különböző sugarú, egymást nem metsző körök:

y 2 + ( x − a cth ⁡ τ ) 2 = a 2 sh 2 ⁡ τ {\displaystyle y^{2}+\left(x-a\operatorname {cth} \tau \right)^{2}={\frac {a^{2}}{\operatorname {sh} ^{2}\tau }}} {\displaystyle y^{2}+\left(x-a\operatorname {cth} \tau \right)^{2}={\frac {a^{2}}{\operatorname {sh} ^{2}\tau }}}

melyek körülveszik a fókuszokat, de szintén nem koncentrikusak. A konstans τ-jú körök középpontjai az x-tengelyen fekszenek. A pozitív τ-hoz tartozó körök a jobb félsíkban (x > 0), míg a negatív τ-jú körök a bal félsíkon (x < 0) találhatók. A τ = 0 egyenes az y-tengely (x = 0). Ahogy τ nő, úgy a körök egyre kisebbek, és középpontjaik megközelítik a fókuszokat.

Thumb
σ értékének változása 0,5-től (lila) π/2 (piros)-ig. Fókuszok a ( − 1 ; 0 ) {\displaystyle (-1;0)} {\displaystyle (-1;0)} és az ( 1 ; 0 ) {\displaystyle (1;0)} {\displaystyle (1;0)} pontokban
Thumb
τ értékének változása 0,5-től (lila) 2 (piros)-ig. Fókuszok a ( − 1 ; 0 ) {\displaystyle (-1;0)} {\displaystyle (-1;0)} és az ( 1 ; 0 ) {\displaystyle (1;0)} {\displaystyle (1;0)} pontokban

Descartes-koordinátákról így lehet bipoláris koordinátákra áttérni:

τ = 1 2 ln ⁡ ( x + a ) 2 + y 2 ( x − a ) 2 + y 2 {\displaystyle \tau ={\frac {1}{2}}\ln {\frac {(x+a)^{2}+y^{2}}{(x-a)^{2}+y^{2}}}} {\displaystyle \tau ={\frac {1}{2}}\ln {\frac {(x+a)^{2}+y^{2}}{(x-a)^{2}+y^{2}}}}

és

π − σ = 2 arctg ⁡ 2 a y a 2 − x 2 − y 2 + ( a 2 − x 2 − y 2 ) 2 + 4 a 2 y 2 . {\displaystyle \pi -\sigma =2\operatorname {arctg} {\frac {2ay}{a^{2}-x^{2}-y^{2}+{\sqrt {(a^{2}-x^{2}-y^{2})^{2}+4a^{2}y^{2}}}}}.} {\displaystyle \pi -\sigma =2\operatorname {arctg} {\frac {2ay}{a^{2}-x^{2}-y^{2}+{\sqrt {(a^{2}-x^{2}-y^{2})^{2}+4a^{2}y^{2}}}}}.}

A koordinátákra vonatkozó további azonosságok:

th ⁡ τ = 2 a x x 2 + y 2 + a 2 {\displaystyle \operatorname {th} \tau ={\frac {2ax}{x^{2}+y^{2}+a^{2}}}} {\displaystyle \operatorname {th} \tau ={\frac {2ax}{x^{2}+y^{2}+a^{2}}}}

és

tg ⁡ σ = 2 a y x 2 + y 2 − a 2 . {\displaystyle \operatorname {tg} \sigma ={\frac {2ay}{x^{2}+y^{2}-a^{2}}}.} {\displaystyle \operatorname {tg} \sigma ={\frac {2ay}{x^{2}+y^{2}-a^{2}}}.}

ami megkapható az x = 0 határértékként a fenti definícióból.

A skálázási tényezők kiszámításához vesszük x + i y {\displaystyle x+iy} {\displaystyle x+iy} egyenletének differenciálját:

d x + i d y = − i a sin 2 ⁡ ( 1 2 ( σ + i τ ) ) ( d σ + i d τ ) . {\displaystyle dx+i\,dy={\frac {-ia}{\sin ^{2}{\bigl (}{\tfrac {1}{2}}(\sigma +i\tau ){\bigr )}}}(d\sigma +i\,d\tau ).} {\displaystyle dx+i\,dy={\frac {-ia}{\sin ^{2}{\bigl (}{\tfrac {1}{2}}(\sigma +i\tau ){\bigr )}}}(d\sigma +i\,d\tau ).}

Ezt az egyenletet komplex konjugáltjával szorozva

( d x ) 2 + ( d y ) 2 = a 2 [ 2 sin ⁡ 1 2 ( σ + i τ ) sin ⁡ 1 2 ( σ − i τ ) ] 2 ( ( d σ ) 2 + ( d τ ) 2 ) . {\displaystyle (dx)^{2}+(dy)^{2}={\frac {a^{2}}{{\bigl [}2\sin {\tfrac {1}{2}}{\bigl (}\sigma +i\tau {\bigr )}\sin {\tfrac {1}{2}}{\bigl (}\sigma -i\tau {\bigr )}{\bigr ]}^{2}}}{\bigl (}(d\sigma )^{2}+(d\tau )^{2}{\bigr )}.} {\displaystyle (dx)^{2}+(dy)^{2}={\frac {a^{2}}{{\bigl [}2\sin {\tfrac {1}{2}}{\bigl (}\sigma +i\tau {\bigr )}\sin {\tfrac {1}{2}}{\bigl (}\sigma -i\tau {\bigr )}{\bigr ]}^{2}}}{\bigl (}(d\sigma )^{2}+(d\tau )^{2}{\bigr )}.}

A szinuszokra és koszinuszok szorzatára vonatkozó azonosságok alkalmazásával

2 sin ⁡ 1 2 ( σ + i τ ) sin ⁡ 1 2 ( σ − i τ ) = cos ⁡ σ − ch ⁡ τ , {\displaystyle 2\sin {\tfrac {1}{2}}{\bigl (}\sigma +i\tau {\bigr )}\sin {\tfrac {1}{2}}{\bigl (}\sigma -i\tau {\bigr )}=\cos \sigma -\operatorname {ch} \tau ,} {\displaystyle 2\sin {\tfrac {1}{2}}{\bigl (}\sigma +i\tau {\bigr )}\sin {\tfrac {1}{2}}{\bigl (}\sigma -i\tau {\bigr )}=\cos \sigma -\operatorname {ch} \tau ,}

ebből

( d x ) 2 + ( d y ) 2 = a 2 ( ch ⁡ τ − cos ⁡ σ ) 2 ( ( d σ ) 2 + ( d τ ) 2 ) . {\displaystyle (dx)^{2}+(dy)^{2}={\frac {a^{2}}{(\operatorname {ch} \tau -\cos \sigma )^{2}}}{\bigl (}(d\sigma )^{2}+(d\tau )^{2}{\bigr )}.} {\displaystyle (dx)^{2}+(dy)^{2}={\frac {a^{2}}{(\operatorname {ch} \tau -\cos \sigma )^{2}}}{\bigl (}(d\sigma )^{2}+(d\tau )^{2}{\bigr )}.}

Eszerint σ és τ skálázási tényezői megegyeznek, és:

h σ = h τ = a ch ⁡ τ − cos ⁡ σ . {\displaystyle h_{\sigma }=h_{\tau }={\frac {a}{\operatorname {ch} \tau -\cos \sigma }}.} {\displaystyle h_{\sigma }=h_{\tau }={\frac {a}{\operatorname {ch} \tau -\cos \sigma }}.}

További eredmények kaphatók az ortogonális koordináta-rendszerek általános egyenletéből behelyettesítéssel. Az infinitezimális területelem:

d A = a 2 ( ch ⁡ τ − cos ⁡ σ ) 2 d σ d τ , {\displaystyle dA={\frac {a^{2}}{\left(\operatorname {ch} \tau -\cos \sigma \right)^{2}}}\,d\sigma \,d\tau ,} {\displaystyle dA={\frac {a^{2}}{\left(\operatorname {ch} \tau -\cos \sigma \right)^{2}}}\,d\sigma \,d\tau ,}

és a Laplace-operátor:

∇ 2 Φ = 1 a 2 ( ch ⁡ τ − cos ⁡ σ ) 2 ( ∂ 2 Φ ∂ σ 2 + ∂ 2 Φ ∂ τ 2 ) . {\displaystyle \nabla ^{2}\Phi ={\frac {1}{a^{2}}}\left(\operatorname {ch} \tau -\cos \sigma \right)^{2}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right).} {\displaystyle \nabla ^{2}\Phi ={\frac {1}{a^{2}}}\left(\operatorname {ch} \tau -\cos \sigma \right)^{2}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right).}

A további differenciáloperátorok, mint ∇ ⋅ F {\displaystyle \nabla \cdot \mathbf {F} } {\displaystyle \nabla \cdot \mathbf {F} } és ∇ × F {\displaystyle \nabla \times \mathbf {F} } {\displaystyle \nabla \times \mathbf {F} } kifejezhetők a ( σ , τ ) {\displaystyle (\sigma ,\tau )} {\displaystyle (\sigma ,\tau )} koordinátákkal úgy, hogy behelyettesítjük a skálázási tényezőket az ortogonális koordináta-rendszerek általános képleteibe.

Az x és y koordináták egyenleteit kombinálva:

x + i y = a i ctg ⁡ ( σ + i τ 2 ) . {\displaystyle x+iy=ai\operatorname {ctg} \left({\frac {\sigma +i\tau }{2}}\right).} {\displaystyle x+iy=ai\operatorname {ctg} \left({\frac {\sigma +i\tau }{2}}\right).}[2][3]

Eszerint a σ és τ koordináták az x+iy analitikus függvény valós és képzetes része. A konform leképezések általános szerint és a Cauchy-Riemann-egyenletekből adódóan a σ és a τ koordinátagörbéi derékszögben metszik egymást.

A bipoláris koordináta-rendszer klasszikus alkalmazásai a parciális differenciálegyenletek megoldását segítik, például Laplace egyenletének vagy a Heimholtz-egyenlet, ahol is a bipoláris koordináták lehetővé teszik a változók szétválasztását. Egy példa a két, különböző átmérőjű hengeres elektromos vezető elektromos mezője.

A poláris nyomtatók bipoláris koordináta-rendszert használnak képek rajzolásához szükséges útvonalak kiszámításához.

A bipoláris koordináták többféleképpen is kiterjeszthetők három dimenzióra az ortogonális tulajdonság megőrzésével:

  • bipoláris hengerkoordináta-rendszer, ahol a harmadik koordináta a z-tengely irányú eltolást jelöli
  • biszférikus koordináta-rendszer, ami az x-tengely, tehát a fókuszokat összekötő tengely körüli forgatással keletkezik
  • toroid koordináta-rendszer, ami az y-tengely, tehát a fókuszokat elválasztó tengely körüli forgatással keletkezik
  1. [1]
    Eric W. Weisstein, Concise Encyclopedia of Mathematics CD-ROM, Bipolar Coordinates, CD-ROM edition 1.0, May 20, 1999 Bipolar Coordinates. [2007. december 12-i dátummal az eredetiből archiválva]. (Hozzáférés: 2006. december 9.)
  2. [2]
    Polyanin, Andrei Dmitrievich. Handbook of linear partial differential equations for engineers and scientists. CRC Press, 476. o. (2002). ISBN 1-58488-299-9
  3. [3]
    Low Reynolds number hydrodynamics: with special applications to particulate media, Mechanics of fluids and transport processes. Springer, 497. o. (1983). ISBN 978-90-247-2877-0
    • "Bipolar coordinates", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
    • Korn GA and Korn TM. (1961) Mathematical Handbook for Scientists and Engineers, McGraw-Hill.

    Ez a szócikk részben vagy egészben a Bipolar coordinates című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

    Edit in WikipediaRevision historyRead in Wikipedia

    Wikiwand in your browser!

    Seamless Wikipedia browsing. On steroids.

    Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.

    Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.

    Chrome
    Wikiwand for Chrome
    Edge
    Wikiwand for Edge
    Firefox
    Wikiwand for Firefox

    Definíció

    Koordinátavonalak

    Kapcsolat a Descartes-koordinátákkal

    Skálázási tényezők

    Az ortogonalitás bizonyítása

    Alkalmazások

    Kiterjesztések három dimenzióra

    Jegyzetek

    Források

    Fordítás