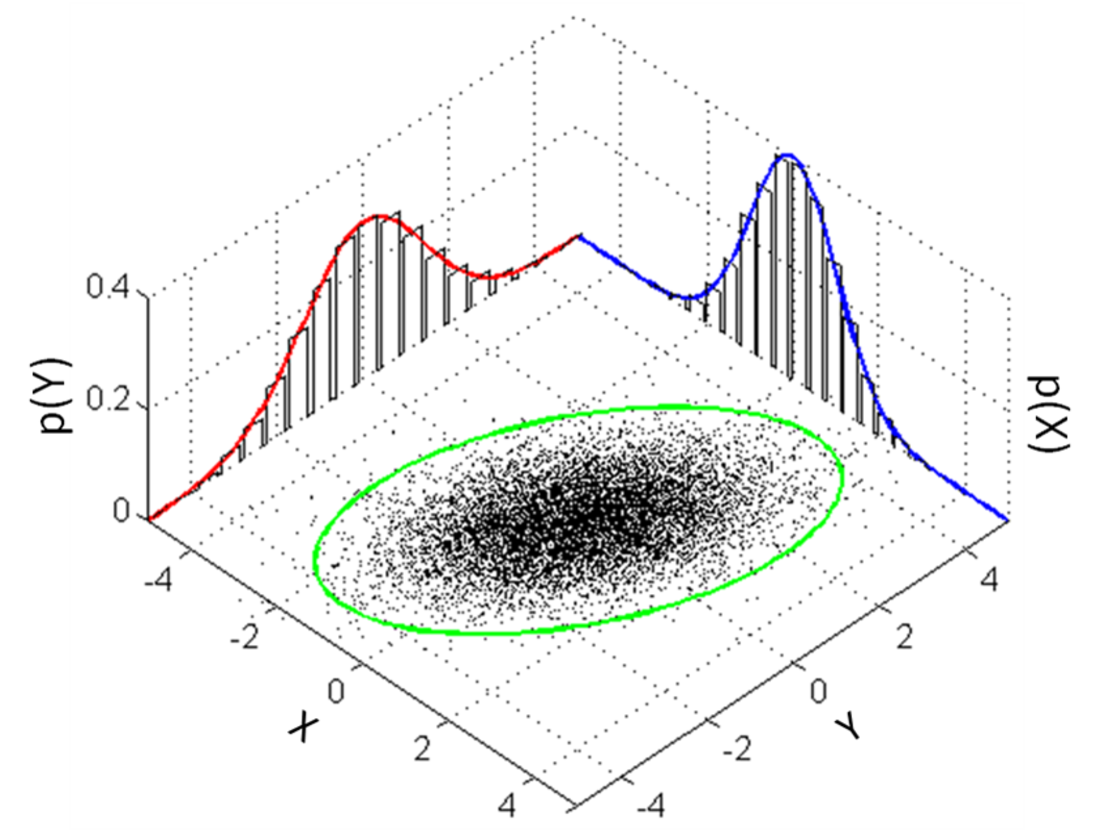
התפלגות רב-נורמלית

בתורת ההסתברות, התפלגות רב-נורמלית, או התפלגות גאוסיאנית רב-ממדית (באנגלית: Multivariate normal distribution) היא הכללה של התפלגות נורמלית למשתנים מקריים רב-ממדיים. היא מוגדרת בתור וקטור משתנים מקריים, שכל צירוף ליניארי שלו מתפלג נורמלית. ישנה גם הגדרה (כללית יותר) בשפה של פונקציות אופייניות (הקובעת את המשתנה).

התפלגות רב-נורמלית

פונקציית צפיפות ההסתברות
מאפיינים
פרמטרים	μ ∈ Rk פרמטר מרכז Σ ∈ Rk × k מטריצת שונות משותפת מטריצה חיובית
תומך	x ∈ Rk
פונקציית צפיפות הסתברות (pdf)	${\displaystyle {\frac {1}{\sqrt {(2\pi )^{n}|{\boldsymbol {\Sigma }}|}}}e^{-({\frac {1}{2}}(\mathbf {x} -{\boldsymbol {\mu }})^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}(\mathbf {x} -{\boldsymbol {\mu }}))}}$
תוחלת	${\displaystyle {\boldsymbol {\mu }}}$
ערך שכיח	${\displaystyle {\boldsymbol {\mu }}}$
שונות	${\displaystyle \ \Sigma }$
אנטרופיה	${\displaystyle {\frac {k}{2}}\log {\mathord {\left(2\pi \mathrm {e} \right)}}+{\frac {1}{2}}\log |{\boldsymbol {\Sigma }}|}$
פונקציה יוצרת מומנטים (mgf)	${\displaystyle \exp \!{\Big (}{\boldsymbol {\mu }}^{\mathrm {T} }\mathbf {t} +{\tfrac {1}{2}}\mathbf {t} ^{\mathrm {T} }{\boldsymbol {\Sigma }}\mathbf {t} {\Big )}}$
פונקציה אופיינית	${\displaystyle \exp \!{\Big (}i{\boldsymbol {\mu }}^{\mathrm {T} }\mathbf {t} -{\tfrac {1}{2}}\mathbf {t} ^{\mathrm {T} }{\boldsymbol {\Sigma }}\mathbf {t} {\Big )}}$

להתפלגות רב-נורמלית מספר שימושים, כגון הוכחת טענות על התפלגות הממוצע וסטיית התקן של משתנים מקריים שווי התפלגות נורמלית; טענות אלו שימושיות במיוחד בסטטיסטיקה. ניתן גם לנסח את משפט הגבול המרכזי בגרסה רב-ממדית בעזרת התפלגות רב-נורמלית.

הגדרה

יהי ${\displaystyle X=(X_{1},\dots ,X_{n})}$ וקטור משתנים מקריים ממשיים. נאמר ש-${\displaystyle X}$ מתפלג רב-נורמלית (או גאוסיאנית) אם לכל ${\displaystyle a_{1},\dots ,a_{n}\in \mathbb {R} }$ המשתנה המקרי (החד־ממדי) ${\displaystyle \langle {\bar {a}},{\bar {X}}\rangle =a_{1}X_{1}+\dots +a_{n}X_{n}}$ מתפלג נורמלית, כלומר קיימים ${\displaystyle \mu ,\sigma }$ (תלויים ב-${\displaystyle a_{i}}$) כך ש-${\displaystyle \langle {\bar {a}},{\bar {X}}\rangle \sim N(\mu ,\sigma ^{2})}$.

אם ${\displaystyle X}$ משתנה רב-נורמלי, מסמנים ${\displaystyle X\sim N({\bar {\mu }},\Sigma )}$. ${\displaystyle {\bar {\mu }}}$ הוא וקטור התוחלות, כלומר

${\displaystyle {\boldsymbol {\mu }}=\operatorname {E} [\mathbf {X} ]=(\operatorname {E} [X_{1}],\operatorname {E} [X_{2}],\ldots ,\operatorname {E} [X_{k}])^{\mathrm {T} }}$

ו-${\displaystyle \Sigma }$ היא מטריצת השונות משותפת

${\displaystyle \Sigma _{i,j}=\operatorname {E} [(X_{i}-\mu _{i})(X_{j}-\mu _{j})]=\operatorname {Cov} [X_{i},X_{j}]}$

כאשר ${\displaystyle 1\leq i,j\leq k}$.

תכונות

הפונקציה האופיינית

ניתן לאפיין את המשתנים המקריים הגאוסיאניים בעזרת הפונקציה האופיינית שלהם: וקטור משתנים מקריים הוא גאוסיאני אם ורק אם הוא בעל פונקציה אופיינית:

$${\displaystyle \varphi _{\mathbf {X} }(\mathbf {u} )=\exp {\Big (}i\mathbf {u} ^{\mathrm {T} }{\boldsymbol {\mu }}-{\tfrac {1}{2}}\mathbf {u} ^{\mathrm {T} }{\boldsymbol {\Sigma }}\mathbf {u} {\Big )}.}$$ כאשר מטריצה השונות ${\displaystyle \Sigma }$ היא חיובית.

בפרט, נובע שהמשתנים המקריים בלתי מתואמים אם ורק אם הם בלתי תלויים (מה שאינו נכון באופן כללי).

לכסון

לכל משתנה מקרי רב-נורמלי ${\displaystyle X}$ קיימים משתנה מקרי ${\displaystyle Y}$ ומטריצה אורתוגונלית ${\displaystyle A}$ כך ש-${\displaystyle X={\bar {\mu }}+YA}$, כאשר ${\displaystyle Y_{i}\sim N(0,\lambda _{i})}$ ו-${\displaystyle \lambda _{i}}$ הם הערכים עצמיים של ${\displaystyle \Sigma }$ (מטריצת השונויות המשותפות).

בכיוון ההפוך, לכל משתנה מקרי רב-נורמלי ${\displaystyle X}$ ולכל מטריצה אורתוגונלית ${\displaystyle A}$, המשתנה המקרי ${\displaystyle AX}$ גם הוא רב נורמלי: ${\displaystyle Y\sim N(A\mu ,\Sigma )}$.

כדי להוכיח משפט זה, יש להפעיל לכסון אורתוגונלי על ${\displaystyle \Sigma }$ (בפרט, המטריצה ${\displaystyle A}$ נבחרת להיות המטריצה המלכסנת).

פונקציית צפיפות

כאשר מטריצת השונות ${\displaystyle \Sigma }$ איננה מטריצה סינגולרית - כלומר כל ערכיה העצמיים ${\displaystyle \lambda _{i}}$ שונים מאפס, למשתנה הרב-נורמלי יש פונקציית צפיפות, הנתונה על ידי הנוסחא:

${\displaystyle f_{X}({\bar {x}})={\frac {1}{\sqrt {(2\pi )^{n}|\Sigma |}}}e^{-{\frac {1}{2}}({\bar {x}}-{\bar {\mu }})^{T}{\Sigma }^{-1}({\bar {x}}-{{\bar {\mu }})}}}$

כאשר ${\displaystyle |\Sigma |=\det(\Sigma )}$ מסמן את הדטרמיננטה של ${\displaystyle \Sigma }$.

התפלגויות שוליות

למציאת ההתפלגות השולית של משתנים מקריים המתפלגים רב-נורמלית, מספיק להשמיט את המשתנים הלא-רלוונטיים (המשתנים שיש לבצע עליהם אינטגרציה) מווקטור התוחלת ${\displaystyle {\boldsymbol {\mu }}}$ וממטריצת השונות ${\displaystyle {\boldsymbol {\Sigma }}}$. ההוכחה לכך נובעת מההגדרה של ההתפלגות הרב-נורמלית ומאלגברה ליניארית.^[1]

דוגמה

יהי ${\displaystyle \mathbf {X} =[X_{1},X_{2},X_{3}]}$ וקטור מקרי רב-נורמלי עם וקטור תוחלת ${\displaystyle {\boldsymbol {\mu }}=[\mu _{1},\mu _{2},\mu _{3}]}$ ומטריצת שונות ${\displaystyle {\boldsymbol {\Sigma }}}$. ההתפלגות השולית של ${\displaystyle \mathbf {X} '=[X_{1},X_{3}]}$ היא התפלגות רב-נורמלית עם וקטור תוחלת ${\displaystyle {\boldsymbol {\mu }}'=[\mu _{1},\mu _{3}]}$ ומטריצת שונות ${\displaystyle {\boldsymbol {\Sigma }}'={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{13}\\{\boldsymbol {\Sigma }}_{31}&{\boldsymbol {\Sigma }}_{33}\end{bmatrix}}}$.

התפלגות רב-נורמלית סינגולרית

בדרך כלל מניחים כי מטריצת השונויות ${\displaystyle \Sigma }$ איננה מטריצה סינגולרית. כאמור, במקרה זה למשתנה הרב-נורמלי יש פונקציית צפיפות.

עם זאת, כאשר מורידים את ההנחה האחרונה (כלומר, יש ערכים עצמיים אפס), מתקבל משתנה מקרי רב-נורמלי סינגולרי. ההגדרה בעזרת הפונקציה האופיינית היא כללית יותר (כלומר, תקפה גם במקרה הסינגולרי). במקרה זה אין פונקציית צפיפות (ביחס למידת לבג) - ערכיה של פונקציית הצפיפות ייקבעו על ידי פחות מ-${\displaystyle n}$ משתנים, ואינטגרל של פונקציה כזו הוא אפס ולא 1, כנדרש מפונקציית צפיפות.

בכל זאת, ניתן להגדיר מידות אחרות (על תת-מרחב ${\displaystyle \operatorname {rank} (\Sigma )}$-ממדי של ${\displaystyle \mathbb {R} ^{n}}$) ואז מוגדרת פונקציית צפיפות עבור משתנה מקרי ביחס למידה החדשה.

יישומים

אם ${\displaystyle X_{1},X_{2},\dots }$ משתנים מקריים בלתי תלויים המתפלגים ${\displaystyle N(0,1)}$, נסמן ${\displaystyle {\bar {X}}_{n}={\frac {X_{1}+\dots +X_{n}}{n}}}$ ו-${\displaystyle S_{n}={\frac {1}{n-1}}\sum _{i=1}^{n}{(X_{i}-{\bar {X}}_{n})^{2}}}$. אז מתקיים:

${\displaystyle {\bar {X}}_{n}/{\sqrt {\frac {S_{n}}{n}}}\sim t_{n-1}}$, כלומר מתפלג סטודנט עם ${\displaystyle n-1}$ דרגות חופש.

קישורים חיצוניים

• התפלגות רב-נורמלית, באתר MathWorld (באנגלית)