Norma (matemáticas)

Nas Matemáticas, unha norma consiste nunha función que a cada elemento dun espazo vectorial lle asocia un número real non-negativo. O concepto de norma está relacionado intuitivamente coa noción xeométrica de lonxitude.

Para outras páxinas con títulos homónimos véxase: Norma.

Unha bóla centrada na orixe de ${\displaystyle \mathbb {R} ^{2}}$ relativa a tres normas distintas.

Definición

Dado un espazo vectorial ${\displaystyle X}$ sobre o corpo ${\displaystyle \mathbb {K} }$ dos números reais ou complexos, unha función ${\displaystyle \|\cdot \|:X\to \mathbb {R} ^{+}}$ é chamada de norma se, para calquera ${\displaystyle {\vec {x}},{\vec {y}}\in X}$ e todo ${\displaystyle \alpha \in \mathbb {K} }$:^[1]

• ${\displaystyle \|{\vec {x}}\|=0\Rightarrow {\vec {x}}={\vec {0}}}$. Se esta condición non for atendida, a función será como máximo unha seminorma.
• ${\displaystyle \|\alpha {\vec {x}}\|=|\alpha |\|{\vec {x}}\|}$
• ${\displaystyle \|{\vec {x}}+{\vec {y}}\|\leq \|{\vec {x}}\|+\|{\vec {y}}\|}$ (desigualdade triangular)

Se o espazo vectorial ${\displaystyle X}$ ten unha norma, pasa a coñecerse como espazo normado, e denótase por ${\displaystyle \left(X,\|\cdot \|\right)}$.

Métrica e topoloxía inducida

Toda norma induce de forma natural unha métrica ${\displaystyle d}$ en ${\displaystyle X}$ que ten valores dados por:^[2]

${\displaystyle d({\vec {x}},{\vec {y}})=\|{\vec {x}}-{\vec {y}}\|\,.}$

Tamén induce unha topoloxía localmente convexa que é xerada por todas as bólas:

${\displaystyle B({\vec {x}}_{0},r)=\{{\vec {x}}\in X:\|{\vec {x}}-{\vec {x}}_{0}\|<r\},~~\forall {\vec {x}}\in X,\forall r\in \mathbb {R_{+}} }$

Normas equivalentes

Dúas normas ${\displaystyle \|.\|_{1}}$ e ${\displaystyle \|.\|_{2}}$ sobre o mesmo espazo vectorial ${\displaystyle X}$ chámanse equivalentes se existiren constantes reais positivas ${\displaystyle C_{1}}$ e ${\displaystyle C_{2}\,(C_{1}\leq C_{2})}$ tales que:

${\displaystyle C_{1}\|{\vec {x}}\|_{1}\leq \|{\vec {x}}\|_{2}\leq C_{2}\|{\vec {x}}\|_{1}~~\forall {\vec {x}}\in X}$

Cando dúas normas son equivalentes, inducen a mesma topoloxía.

Normas en espazos de dimensión finita

Sexa ${\displaystyle {\vec {x}}=\left(x_{1},x_{2},\ldots ,x_{n}\right)=\sum _{i=1}^{n}x_{i}{\vec {e}}_{i}}$ a representación dun vector en ${\displaystyle \mathbb {R} ^{n}}$ ou ${\displaystyle \mathbb {C} ^{n}}$.

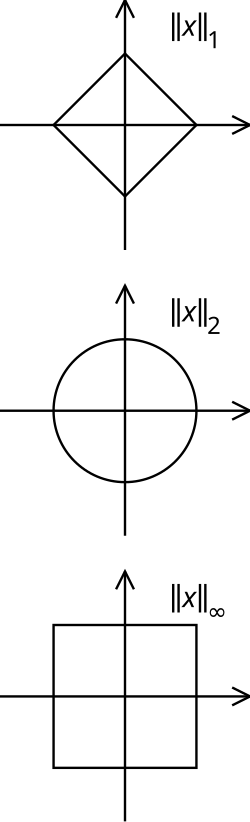
As normas canónicas definidas nestes espazos son as chamadas normas ${\displaystyle \ell ^{p}}$:

• ${\displaystyle \|{\vec {x}}\|_{p}=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}~~,1\leq p<\infty }$
• ${\displaystyle \|{\vec {x}}\|_{\infty }=\max _{i=1}^{n}(|x_{i}|)}$

O caso particular no que ${\displaystyle p=2}$ corresponde á norma euclidiana:

${\displaystyle \left(\sum _{i=1}^{n}|x_{i}|^{2}\right)^{1/2}=\|{\vec {x}}\|_{2}={\sqrt {|x_{1}|^{2}+\ldots +|x_{n}|^{2}}}}$

A norma euclidiana é a que mide a distancia entre dous puntos do plano usada habitualmente ${\displaystyle \|{\vec {x}}\|={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}$.

Pódense definir tamén outras normas, mais pódese demostrar que serán equivalentes.

Norma matricial

Se o espazo vectorial considerado é o formado polas matrices reais ou complexas de orde ${\displaystyle n\times m}$, denotado por ${\displaystyle M^{n\times m}}$, unha norma sobre ese espazo é chamada de norma matricial.

Un exemplo de norma matricial é a norma 1, denotada ${\displaystyle \|.\|_{1}}$ definida como o máximo da suma módulo dos elementos de cada liña, ou sexa se ${\displaystyle A=\left[a_{ij}\right]_{r\times s}}$ entón a norma do máximo da matriz ${\displaystyle A}$ é o número non negativo dado por

${\displaystyle \|A\|_{1}=\max _{1\leq i\leq r}\sum _{j=1}^{s}|a_{ij}|.}$

A norma do máximo da matriz ${\displaystyle A={\begin{vmatrix}1&3\\2&-1\end{vmatrix}}}$, por exemplo, é^[3]

${\displaystyle \|A\|_{1}=\max \left\{|1|+|3|,|2|+|-1|\right\}=\max \left\{4,3\right\}=4.}$

Normas en espazos de dimensión infinita

Espazos L^P

Artigo principal: Espazo Lp.

As normas ${\displaystyle \ell ^{p}}$ teñen análogos nalgúns espazos de dimensión infinita.

Notas

1. SANTOS (2010), p.3, ex. 54.
2. SANTOS (2010), p.60.
3. Boldrini et. al, p. 342.

Véxase tamén

Bibliografía

• Santos, José Carlos (xuño de 2010). Introduçión à Topologia (PDF). Porto: Departamento de Matemática - Faculdade de Ciencias da Universidade do Porto. p. 171.
• Boldrini, José Luiz et. al. Álgebra Linear (3ª ed.). Harbra. p. 342.

Outros artigos

• Produto interno
• Espazo de Banach
• Espazo euclidiano
• Espazo métrico
• Espazo topolóxico
• Seminorma