Triangle orthique

En géométrie, le triangle orthique d'un triangle de référence est le triangle ayant pour sommets les pieds des hauteurs du triangle de référence.

Propriétés

Dans un triangle ${\displaystyle ABC}$ acutangle (triangle non rectangle dont les trois angles sont aigus), les hauteurs, concourantes en son orthocentre ${\displaystyle H}$, sont les bissectrices du triangle orthique ${\displaystyle h_{A}h_{B}h_{C}}$ ^[1]. Il en résulte que, dans un tel triangle, l'orthocentre est le centre du cercle inscrit dans le triangle orthique, et les sommets sont donc les centres des cercles exinscrits du triangle orthique. Le triangle orthique est également le triangle podaire et le triangle cévien de l'orthocentre pour le triangle de référence.

Les quadruplets de points ${\displaystyle (C,B,h_{C},h_{B})}$ ; ${\displaystyle (B,A,h_{B},h_{A})}$ et ${\displaystyle (A,C,h_{A},h_{C})}$ sont cocycliques. Les centres des cercles en question sont les milieux des côtés du triangle ${\displaystyle ABC}$ (selon le théorème de Thalès pour le cercle).

Ainsi, on en déduit les valeurs des angles au sommet du triangle orthique :

${\displaystyle {\widehat {h_{B}h_{A}h_{C}}}=\pi -{\widehat {BAC}},\ {\widehat {h_{A}h_{C}h_{B}}}=\pi -{\widehat {ACB}},\ {\widehat {h_{C}h_{B}h_{A}}}=\pi -{\widehat {CBA}}}$

On a les égalités d'angles inscrits^[1] :

${\displaystyle {\widehat {h_{B}h_{A}A}}={\widehat {h_{B}BA}}={\widehat {ACh_{C}}}={\widehat {Ah_{A}h_{C}}}}$

Les longueurs des côtés du triangle orthique sont :

${\displaystyle h_{A}h_{B}=R\sin(2{\widehat {BAC}})=BC\cos({\widehat {BAC}}),\ h_{B}h_{C}=R\sin(2{\widehat {ABC}})=AC\cos({\widehat {ABC}}),\ h_{C}h_{A}=R\sin(2{\widehat {ACB}})=AB\cos({\widehat {ACB}}),\ }$

ou R est le rayon du cercle circonscrit à ABC. Son aire est :

${\displaystyle S={\frac {R^{2}}{2}}\sin(2{\widehat {BAC}})\sin(2{\widehat {CBA}})\sin(2{\widehat {ACB}})}$

Le rayon de son cercle inscrit est :

${\displaystyle r_{orthic}=2R\cos({\widehat {BAC}})\cos({\widehat {CBA}})\cos({\widehat {ACB}})}$

et celui de son cercle circonscrit est :

${\displaystyle R_{orthic}=R/2}$

Perpendiculaires et parallèles aux côtés du triangle orthique

Les côtés du triangle orthique sont perpendiculaires aux rayons joignant le centre du cercle circonscrit aux sommets du triangle ${\displaystyle ABC}$.

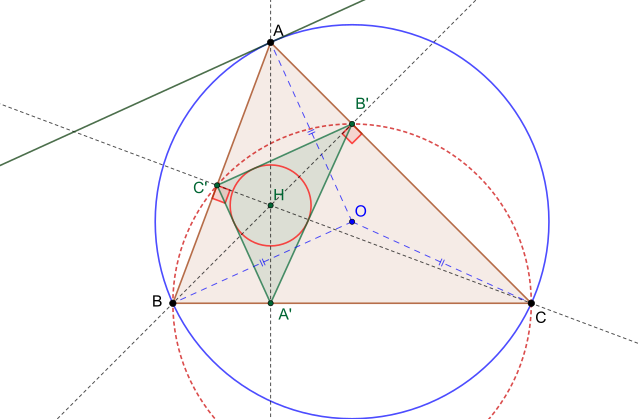
On note ${\displaystyle O}$ le centre du cercle circonscrit au triangle ${\displaystyle ABC}$ de centre ${\displaystyle O}$, et ${\displaystyle A',B',C'}$ les pieds des hauteurs issues de ${\displaystyle A,B,C}$ respectivement.

Une étude des angles inscrits permet de montrer que ${\displaystyle (B'C')}$ est parallèle à la tangente au cercle circonscrit en ${\displaystyle A}$. Donc ${\displaystyle (OA)}$ est perpendiculaire à ${\displaystyle (B'C')}$. On montre aussi que cette tangente est parallèle à la droite de Simson du point intersection de ${\displaystyle (AH)}$ avec le cercle circonscrit^[2].

De même ${\displaystyle (OB)}$ est perpendiculaire à ${\displaystyle (A'C')}$ et ${\displaystyle (OC)}$ est perpendiculaire à ${\displaystyle (A'B')}$.

On peut résumer ceci en :

Les tangentes au cercle circonscrit passant par les sommets du triangle sont parallèles aux côtés du triangle orthique.

Le triangle formé par les tangentes au cercle circonscrit est le triangle tangentiel, ses côtés sont donc parallèles à ceux du triangle orthique.

Le triangle A'B'C' est le triangle orthique de ABC, le triangle A₁B₁C₁ est son triangle tangentiel .

Le triangle orthique est l'unique trajectoire d'un balle sur un billard triangulaire qui se referme en trois rebonds^[3],[4].

On peut aussi en déduire que les côtés du triangle orthique sont antiparallèles aux côtés du triangle deux à deux^[5].

Problème de Fagnano

Le triangle orthique est la solution au problème d'optimisation visant à trouver le triangle inscrit dans un triangle qui a le plus petit périmètre.

Triangle médian du triangle orthique

Soit un triangle ${\displaystyle ABC}$ non rectangle, soient ${\displaystyle A',B',C'}$ les pieds des hauteurs du triangle ${\displaystyle ABC}$ issues respectivement de ${\displaystyle A,B,C}$ ; on note ${\displaystyle A_{1}}$ et ${\displaystyle A_{2}}$ les projections orthogonales de ${\displaystyle A'}$ sur ${\displaystyle (AB)}$ et ${\displaystyle (AC)}$, ${\displaystyle A_{3}}$ et ${\displaystyle A_{4}}$ les symétriques de ${\displaystyle A'}$ par rapport à ${\displaystyle A_{1}}$ et ${\displaystyle A_{2}}$.

La droite ${\displaystyle (A_{3}A_{4})}$ est parallèle à ${\displaystyle (A_{1}A_{2})}$, les points ${\displaystyle B',C',A_{3},A_{4}}$ sont alignés, la droite ${\displaystyle (A_{1}A_{2})}$ contient les milieux ${\displaystyle Q}$ et ${\displaystyle R}$ des côtés ${\displaystyle [A'C']}$et ${\displaystyle [A'B']}$ du triangle orthique de ${\displaystyle ABC}$ , ${\displaystyle (A_{1}A_{2})}$ est un des côtés de ${\displaystyle PQR}$, triangle médian du triangle orthique.

A₃A₄ est égal au périmètre du triangle orthique ${\displaystyle A'B'C'}$. Ce périmètre est égal à ${\displaystyle {\frac {8S^{2}}{abc}}}$ où ${\displaystyle S}$est l'aire du triangle ${\displaystyle ABC}$ et ${\displaystyle a,b,c}$ sont les longueurs des côtés de ${\displaystyle ABC}$.

Références

1. Patrice Debart, « Triangle orthique », sur debart.fr
2. Trajan Lalesco, La géométrie du triangle, Jacques Gabay, 1987 (ISBN 2-87647-007-1), p. 10
3. Elisabeth Busser et Gilles Cohen, 100 Jeux mathématiques du «Monde», Pole, coll. « Jeux - Tests et maths », 2007, énoncé p. 70, solution p.99.
4. Peyrol Caroline (Coordinnatrice) et Équipe d'élèves et d'enseignants des lycées Paul Eluard de Saint-Denis (93), Jacques Feyder d'Epinay sur Seine et du collège Jean Vilar de Villetaneuse, « Trajectoires périodiques et billard triangulaire », dans Actes du congrès “MATh.en.JEANS” en 1996, 1996 (lire en ligne), p. 129-130.
5. (en) Florentin Smarandache et Ion Patrascu, The Geometry of the Orthological triangles (lire en ligne)

Articles connexes

• Problème de Fagnano
• Axe orthique

Sources

• Démonstrations : Sortais Yvonne et René, La géométrie du triangle, Hermann, 1997.
• (en) Eric W. Weisstein, « Orthic Triangle », sur MathWorld

Bibliographie

• Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4)

• Portail de la géométrie