Une surface de Catalan est une surface réglée dont les génératrices restent parallèles à un plan fixe appelé plan directeur.
Ces surfaces ont été étudiées par le mathématicien belge Eugène Charles Catalan (1814-1894).
Surface de Catalan. Les équations paramétriques d'une surface de Catalan de plan directeur
x
⋅
n
0
=
0
{\displaystyle \mathbf {x} \cdot \mathbf {n} _{0}=0}
[1]
x
(
u
,
v
)
=
c
(
u
)
+
v
r
(
u
)
,
{\displaystyle \mathbf {x} (u,v)=\mathbf {c} (u)+v\mathbf {r} (u)\ ,}
r
(
u
)
⋅
n
0
=
0
{\displaystyle \mathbf {r} (u)\cdot \mathbf {n} _{0}=0}
Chaque droite
x
(
u
0
,
v
)
{\displaystyle \mathbf {x} (u_{0},v)}
u
=
u
0
{\displaystyle u=u_{0}}
c
(
u
)
{\displaystyle \mathbf {c} (u)}
r
(
u
)
{\displaystyle \mathbf {r} (u)}
Si
r
(
u
)
{\displaystyle \mathbf {r} (u)}
det
(
r
,
r
˙
,
r
¨
)
=
0
{\displaystyle \det(\mathbf {r} ,\mathbf {\dot {r}} ,\mathbf {\ddot {r}} )=0}
(1) Les plans :
x
(
u
,
v
)
=
p
+
u
a
+
v
r
{\displaystyle \mathbf {x} (u,v)=\mathbf {p} +u\mathbf {a} +v\mathbf {r} }
La courbe directrice est une droite.
(2) Les cylindres :
x
(
u
,
v
)
=
(
cos
u
,
sin
u
,
0
)
+
v
(
0
,
0
,
1
)
{\displaystyle \mathbf {x} (u,v)=(\cos u,\sin u,0)+v(0,0,1)}
La courbe directrice est un cercle. Comme plan directeur, on peut prendre tout plan parallèle à l'axe des z.
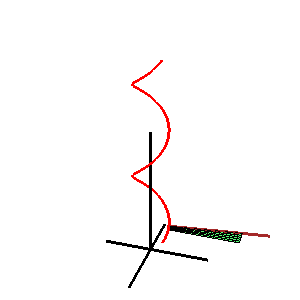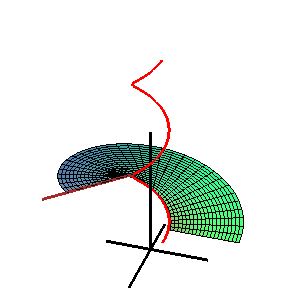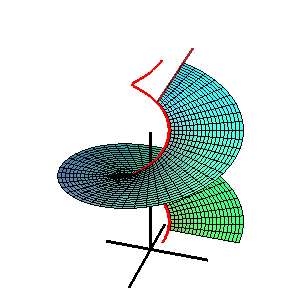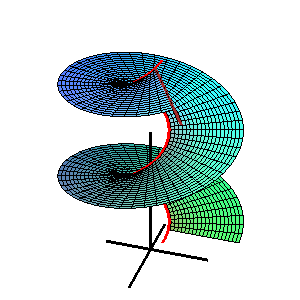
(3) L'hélicoïde :
x
(
u
,
v
)
=
(
cos
u
,
sin
u
,
u
)
+
v
(
cos
u
,
sin
u
,
0
)
{\displaystyle \mathbf {x} (u,v)=(\cos u,\sin u,u)+v(\cos u,\sin u,0)}
La courbe directrice est une hélice et le plan directeur est parallèle au plan x-y.
Cette surface peut aussi être définie à partir d'une droite (axe des z) comme courbe directrice:
x
(
u
,
v
)
=
(
0
,
0
,
u
)
+
v
(
cos
u
,
sin
u
,
0
)
{\displaystyle \mathbf {x} (u,v)=(0,0,u)+v(\cos u,\sin u,0)}
(4) Si toutes les génératrices d'une surface de Catalan coupent une droite fixe, alors la surface est appelée un conoïde . Catalan a prouvé que l'hélicoïde et le plan sont les seules surfaces minimales réglées .
A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica , 3rd ed. Boca Raton, FL:CRC Press, 2006. (ISBN 9781584884484
(en) « Surface de Catalan » , dans Michiel Hazewinkel , Encyclopædia of Mathematics Springer , 2002 (ISBN 978-1556080104 lire en ligne ) V. Y. Rovenskii, Geometry of curves and surfaces with MAPLE (ISBN 978-0-8176-4074-3 
