Réseau de Petri

Un réseau de Petri^[1] (aussi connu comme un réseau de Place/Transition ou réseau de P/T) est un modèle mathématique servant à représenter divers systèmes (informatiques, industriels…) travaillant sur des variables discrètes.

Le problème du dîner des philosophes modélisé en Réseau de Petri

Exemple d'un réseau de Petri Place-Transition, composé de : deux places, les cercles trois transitions, les traits noirs quatre arcs, les flèches deux jetons, les points noirs qui circulent de gauche à droite

Les réseaux de Petri sont apparus en 1962, dans la thèse de doctorat de Carl Adam Petri. Les réseaux de Petri sont des outils graphiques et mathématiques permettant de modéliser et de vérifier le comportement dynamique des systèmes à événements discrets comme les systèmes manufacturiers, les systèmes de télécommunications, les réseaux de transport.

Le diagramme d'activité UML et le Grafcet sont des dérivés simplifiés de réseau de Petri, mis à part qu'à un modèle basé sur un réseau de Petri est associée une représentation mathématique de matrices de transitions d'état permettant d'assurer des preuves formelles de théorie des graphes, d'algèbre temporelle et de processus stochastiques markoviens.

Définition

Un réseau de Petri est un 6-uplet ${\displaystyle (S,T,F,M_{0},W,K)\,}$, où^[2] :

• ${\displaystyle S}$ définit une ou plusieurs places.
• ${\displaystyle T}$ définit une ou plusieurs transitions.
• ${\displaystyle F}$ définit un ou plusieurs arcs (flèches).

Un arc ne peut pas connecter deux places ni deux transitions, il ne peut connecter que des paires place-transition ; plus formellement : ${\displaystyle F\subseteq (S\times T)\cup (T\times S)}$.

• ${\displaystyle M_{0}:S\to \mathbb {N} }$ appelé marquage initial, où, pour chaque place ${\displaystyle s\in S}$, il y a ${\displaystyle n\in \mathbb {N} }$ jetons.
• ${\displaystyle W:F\to \mathbb {N^{+}} }$ appelé ensemble d'arcs primaires , assignant à chaque arc ${\displaystyle f\in F}$ un entier positif ${\displaystyle n\in \mathbb {N^{+}} }$ qui indique combien de jetons sont consommés depuis une place vers une transition, ou sinon, combien de jetons sont produits par une transition et arrivent pour chaque place.
• ${\displaystyle K:S\to \mathbb {N^{+}} }$ appelé limite de capacité, faisant correspondre à chaque place ${\displaystyle s\in S}$ un nombre positif ${\displaystyle n\in \mathbb {N^{+}} }$ représentant le nombre maximum de jetons qui peuvent occuper une place.

De nombreuses définitions formelles existent. Cette définition concerne un réseau place-transition (ou P-T). D'autres définitions n'incluent pas la notion d'arc primaire ou la limite de capacité.

Représentation

Détail d'un réseau de Petri

Un réseau de Petri se représente par un graphe biparti (composé de deux types de nœuds et dont aucun arc ne relie deux nœuds de même type) orienté (composé d'arc(s) ayant un sens) reliant des places et des transitions (les nœuds). Deux places ne peuvent pas être reliées entre elles, ni deux transitions. Les places peuvent contenir des jetons, représentant généralement des ressources disponibles.

La distribution des jetons dans les places est appelée le marquage du réseau de Petri.

Les entrées d'une transition sont les places desquelles part une flèche pointant vers cette transition, et les sorties d'une transition sont les places pointées par une flèche ayant pour origine cette transition.

Représentation matricielle

La définition matricielle introduit les matrices ${\displaystyle PRE\in {\mathcal {M}}_{mn}}$ et ${\displaystyle POST\in {\mathcal {M}}_{mn}}$.

• ${\displaystyle PRE_{pt}=W(p,t)}$
• ${\displaystyle POST_{pt}=W(t,p)}$

Ces matrices de même dimension représentent en ligne les places, et en colonne les transitions. ${\displaystyle PRE}$ contient les valuations des arcs qui vont des places vers les transitions, ${\displaystyle POST}$ concerne les arcs des transitions vers les places. Une valeur nulle dans une des matrices indique l'inexistence d'un arc dans un sens ou dans l'autre.

La matrice d'incidence ${\displaystyle C}$ est définie par ${\displaystyle C=POST-PRE}$. Étant donné une transition ${\displaystyle t}$, ${\displaystyle C_{pt}}$ est le nombre de jetons qui seront ajoutés (ou retirés si le nombre est négatif) à la place ${\displaystyle p}$ si la transition ${\displaystyle t}$ est franchie.

Dynamique d'exécution

Un réseau de Petri évolue lorsqu'on exécute une transition : des jetons sont retirés dans les places en entrée de cette transition et des jetons sont déposés dans les places en sortie de cette transition.

L'exécution d'une transition (pour un réseau de base ou un réseau coloré) est une opération indivisible qui est déterminée par la présence du jeton sur la place d'entrée.

L'exécution d'un réseau de Petri n'est pas déterministe, car il peut y avoir plusieurs possibilités d'évolution à un instant donné (ex. : pour une place en amont de deux transitions concurrentes).

Si chaque transition dans un réseau de Petri a exactement une entrée et une sortie alors ce réseau est un automate fini.

Franchissement d'une transition

Le fait que la transition ${\displaystyle t}$ est franchissable à partir du marquage ${\displaystyle M}$ se note ${\displaystyle M{\stackrel {t}{\rightarrow }}}$

On dit qu'une transition ${\displaystyle t}$ est franchissable, si chaque place ${\displaystyle p}$ en entrée contient un nombre de jetons supérieur ou égal à la valuation de l'arc qui la relie à la transition ${\displaystyle t}$. C'est-à-dire :

${\displaystyle M\geq PRE_{t}}$

Note : ${\displaystyle PRE_{t}}$ est la t-ième colonne de ${\displaystyle PRE}$.

Le franchissement d'une transition permet d'atteindre un nouveau marquage ${\displaystyle M'}$ à partir de ${\displaystyle M}$ : ${\displaystyle M{\stackrel {t}{\rightarrow }}M'}$ :

${\displaystyle M'=M+C_{t}}$

Séquence de transitions

Une séquence de transitions est une séquence formée sur l'alphabet des transitions (voir Langage formel). Elle décrit une suite de transitions à activer.

On dit qu'une séquence de transitions ${\displaystyle \sigma =\sigma 't}$ est franchissable à partir du marquage M si :

• ${\displaystyle \sigma '}$ est franchissable à partir de M et ${\displaystyle M{\stackrel {\sigma '}{\rightarrow }}M'}$
• t est franchissable à partir de M', ${\displaystyle M'{\stackrel {t}{\rightarrow }}}$

À une séquence de transitions ${\displaystyle \sigma }$, on associe un vecteur commutatif ${\displaystyle {\stackrel {\rightarrow }{\sigma }}=(\alpha _{1},...,\alpha _{m})}$ (m est le nombre de transitions). ${\displaystyle \alpha _{i}}$ est le nombre d'occurrences de la transition i dans ${\displaystyle \sigma }$.

Exemple : Soit un réseau avec les transitions ${\displaystyle T=\{t_{1},t_{2},t_{3}\}}$. ${\displaystyle \sigma =t_{2}t_{1}t_{3}t_{1}}$, le vecteur commutatif correspondant est ${\displaystyle {\stackrel {\rightarrow }{\sigma }}=(2,1,1)}$ (vecteur colonne)

Si la séquence ${\displaystyle \sigma }$ est franchissable à partir du marquage M, alors on peut calculer le marquage M' obtenu par ${\displaystyle \sigma {\stackrel {t}{\rightarrow }}}$ :

${\displaystyle M'=M+C.{\stackrel {\rightarrow }{\sigma }}}$

Représentation graphique

Graphe de marquage

Le graphe des marquages d'un réseau ${\displaystyle (R,M_{0})}$ est un graphe orienté dont les nœuds sont les marquages de ${\displaystyle A(R,M_{0})}$, et chaque arc relie un marquage à un autre qui est immédiatement accessible par une transition : si ${\displaystyle M_{0}{\stackrel {t}{\rightarrow }}M_{1}}$, un arc est tracé de ${\displaystyle M_{0}}$ à ${\displaystyle M_{1}}$ et il est marqué avec ${\displaystyle t}$.

Ce type de graphe donne une vue simple de l'évolution d'un réseau, néanmoins le graphe des marquages n'est pertinent que pour les réseaux bornés^[3] : un réseau non borné a une infinité de marquages et ne pourrait être représenté.

L'algorithme de construction du graphe se définit récursivement, partant de l'état initial, on détermine de proche en proche les marquages accessibles.

• S est l'ensemble des nœuds du graphe, il est initialisé à ${\displaystyle M_{0}}$
• En entrée, l'algorithme prend un marquage ${\displaystyle M}$

Pour toute transition t faire
 Si ${\displaystyle M{\stackrel {t}{\rightarrow }}M_{1}}$ Alors
   Si ${\displaystyle M_{1}\notin S}$ Alors
     ${\displaystyle S\leftarrow S\bigcup \{M_{1}\}}$
     Créer le sommet ${\displaystyle M_{1}}$
   Fin Si
   Créer l'arc ${\displaystyle (M,M_{1})}$
   Appeler l'algorithme avec ${\displaystyle M_{1}}$
 Fin Si
Fin Pour

Graphe de Petri

Graphe de couverture

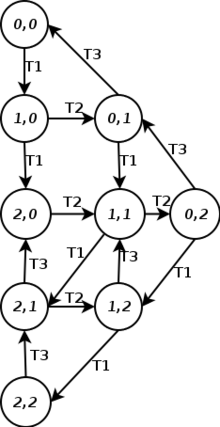
Un graphe de couverture est semblable à un graphe de marquage dans lequel on va utiliser un symbole, par exemple ${\displaystyle \omega }$, pour indiquer la présence d'un nombre arbitrairement grand de jetons (en pratique une infinité) : une transition peut alors prélever et ajouter librement des jetons sur cette place. Il s'agit cependant d'une sur-approximation et certaines transitions paraissant possibles sur le graphe de couverture peuvent ne pas l'être en pratique.

Propriétés mathématiques des réseaux de Petri

L'un des intérêts des réseaux de Petri provient de l'équilibre entre leur capacité de modélisation et la complexité de leur analyse. De nombreuses propriétés que l'on désirerait obtenir pour des systèmes concurrents sont automatiquement déterminées pour des réseaux de Petri même si certaines peuvent être coûteuses en termes de calcul dans le cas général. Plusieurs sous-classes de réseaux de Petri ont donc été étudiées afin de modéliser diverses classes de systèmes concurrents tout en facilitant la détermination de ces propriétés.

Pour une présentation plus complète de la décidabilité et de la complexité des problèmes sur les réseaux de Petri, le lecteur se reportera à l'article de Esparza et Nielsen ^[4].

Accessibilité

Le problème d'accessibilité pour les réseaux de Petri revient à décider, pour un réseau ${\displaystyle N}$ et un marquage ${\displaystyle M}$ si ${\displaystyle M\in R(N).}$.

Il s'agit évidemment d'un problème de chemin sur le graphe de marquage défini ci-dessus, ou bien jusqu'à ce que l'on atteigne le marquage ${\displaystyle M}$ ou que l'on sache qu'il ne peut pas être atteint. Ce problème est en général beaucoup plus difficile qu'il n'y parait car le graphe de marquage est généralement infini et il n'est pas évident de déterminer quand l'on peut s'arrêter de chercher.

Bien que l'accessibilité semble être une bonne manière de trouver les états défectueux (par exemple pour prouver la correction d'un programme), dans les cas pratiques la construction du graphe de marquage est beaucoup trop complexe. Pour simplifier ce problème, on recourt donc à la logique temporelle linéaire en complément de méthode d'analyse des tableaux pour prouver que ces états ne peuvent être atteints. La logique temporelle utilise des méthodes de semi-décision pour déterminer un ensemble de conditions nécessaire à l'accessibilité de l'état avant de prouver que ces conditions ne peuvent être satisfaites.

Détermination des bornes

Une place d'un réseau de Petri est dite k-bornée si elle ne contient pas plus de ${\displaystyle k}$ jetons dans l'ensemble des marquages accessibles, y compris le marquage initial. Elle est dite sûre si elle est 1-bornée et bornée si elle est k-bornée pour un entier ${\displaystyle k}$.

Extensions

Un réseau de Petri de haut niveau est un réseau coloré et hiérarchique.

Couleur

Pour un réseau de Petri de base, on ne distingue pas les différents jetons. Dans un réseau de Petri coloré, on associe une valeur à chaque jeton.

Pour plusieurs outils associés aux réseaux de Petri colorés, les valeurs des jetons sont typées, et peuvent être testées et/ou manipulées avec un langage fonctionnel.

Hiérarchie

Une autre extension du réseau de Petri est la hiérarchie (ou récursivité) : des éléments du réseau de Petri sont eux-mêmes composés d'un réseau de Petri.

Stochastique

Les réseaux de Petri stochastiques ajoutent de l'indéterminisme.

Notes et références

1. en français on prononce [petʁi̩]
2. (en) Jörg Desel et Gabriel Juhás, « What is a Petri net? Informal answers for the informed reader », Lecture Notes in Computer Science, Springer, vol. 2128 « Unifying Petri Nets – Advances in Petri Nets »,‎ 2001, p. 1-25 (DOI 10.1007/3-540-45541-8_1, résumé).
3. réseau dont toutes les places atteignables ont un nombre fini de jetons
4. Javier Esparza et Mogens Nielsen, « Decidability issues for Petri nets – a survey », Bulletin of the EATCS,‎ 1995 (lire en ligne, consulté le 14 mai 2014)

Bibliographie

Bibliographie francophone

• G.W. Brams, Réseaux de Petri : Théorie et Pratique, Masson, 1983. (ISBN 2-903607-12-5)
• Annie Choquet-Geniet, Les réseaux de Petri : Un outil de modélisation, Paris, Éditions Dunod, coll. « Sciences Sup », 7 mars 2006, 240 p. (ISBN 2-10-049147-4)
• René David et Hassane Alla, Du Grafcet aux réseaux de Petri, Paris, Hermès, 1992, 2^e éd., 500 p. (ISBN 2-86601-325-5)
  à noter l'ouvrage en anglais traitant plus spécialement des extensions temporelles et continues : René David et Hassane Alla, Discrete, Continuous, and Hybrid Petri Nets, Berlin, Springer-Verlag, 2005 (ISBN 3-540-22480-7)
• Michel Diaz, Vérification et mise en œuvre des réseaux de Petri : ouvrage collectif sous la direction de Michel Diaz, Hermes Science Publications, coll. « Traité IC2 / Informatique et systèmes d'information » (ISBN 978-2-7462-0445-4 et 2-7462-0445-2)
• M. Combacau et P. Esteban, Commandes à Réseaux de Petri, coll. « Techniques de l'Ingénieur », 10 mars 2005 (lire en ligne)
• Marc Bourcerie, Réseaux de Petri, Elaboration pour les systèmes de production, cours et exercices corrigés, Éditions Ellipses, coll."technosup", février 2011
• Marion Juan, David Mailland, Nicolas Fifis et Guy Gregoris, Modélisation des pannes d’une antenne active et modifications d’architecture, coll. « Techniques de l'Ingénieur », 10 décembre 2021 (lire en ligne)

Autres langues

• Janette Cardoso et Heloisa Camargo, Fuzziness in Petri Nets, Physica-Verlag, 1999, 318 p. (ISBN 3-7908-1158-0, lire en ligne).
• (en) Kurt Jensen, Coloured Petri Nets : basic concepts, analysis methods, and practical use, Berlin/Heidelberg/Paris etc., Springer Verlag, 1997, 265 p. (ISBN 3-540-62867-3).
• Вадим Котов, Сети Петри (Petri Nets, in Russian), Наука, Москва,‎ 1984.
• András Pataricza, Formális módszerek az informatikában (Formal methods in informatics), TYPOTEX Kiadó, 2004 (ISBN 963-9548-08-1).
• Carl Adam Petri et Wolfgang Reisig, « Petri net », Scholarpedia 3(4):6477 (consulté le 13 juillet 2008)
• Wolfgang Reisig, A Primer in Petri Net Design, Springer-Verlag, 1992 (ISBN 3-540-52044-9).
• Robert-Christoph Riemann, Modelling of Concurrent Systems : Structural and Semantical Methods in the High Level Petri Net Calculus, Herbert Utz Verlag, 1999, 252 p. (ISBN 3-89675-629-X, lire en ligne).
• Harald Störrle, Models of Software Architecture : Design and Analysis with UML and Petri-Nets, Books on Demand, 2000 (ISBN 3-8311-1330-0). With courtesy of the author, freely available online.
• (en) Mengchu Zhou et Frank Dicesare, Petri Net Synthesis for Discrete Event Control of Manufacturing Systems, Boston/Dordrecht/London, Kluwer Academic Publishers, 1993, 233 p. (ISBN 0-7923-9289-2).
• Mengchu Zhou, Kurapati Venkatesh, Modeling, Simulation, & Control of Flexible Manufacturing Systems : A Petri Net Approach, World Scientific Publishing, 1998 (ISBN 981-02-3029-X).
• Dmitry Zaitsev, Clans of Petri Nets : Verification of protocols and performance evaluation of networks, LAP LAMBERT Academic Publishing, 2013 (ISBN 978-3-659-42228-7, lire en ligne).

Liens externes

• « PetriParC - GDR MACS », sur www.univ-valenciennes.fr/gdr-macs
• « Groupe francophone de recherche sur les réseaux de Petri », sur lagis.ec-lille.fr
• TINA - TIme petri Net Analyser, sur www.laas.fr

• Portail de la robotique
• Portail de l’électricité et de l’électronique
• Portail de l'informatique théorique