Miroir sphérique

Un miroir sphérique est un miroir dont la forme est une calotte sphérique, c'est-à-dire une sphère tronquée par un plan. L'ouverture du miroir est donc un disque, et son axe optique est la droite normale à l'ouverture et passant par son centre.

Miroir sphérique

modifier - modifier le code - modifier Wikidata

Il existe des miroirs sphériques convexes et concaves.

Astigmatisme

Miroir sphérique concave hors des conditions de Gauss : les rayons émergents ne convergent pas.

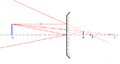
Le miroir sphérique est astigmatique, c'est-à-dire que des rayons issus d'un même point source ne convergent pas.

Il n'est stigmatique que pour son centre qui est sa propre image.

Conditions de Gauss

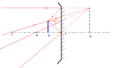
Représentation du miroir dans les conditions du stigmatisme approché : on dit que le miroir est dans les conditions de Gauss si les rayons incidents sont paraxiaux (autrement dit, s'ils frappent le miroir très près du sommet en faisant un angle très petit avec l'axe du miroir).

Utilisé dans les conditions de Gauss, un miroir sphérique est approximativement stigmatique et aplanétique.

Points et rayons particuliers :

• un rayon passant par le foyer F est réfléchi parallèlement à l'axe optique ;
• un rayon incident parallèle à l'axe optique est réfléchi en passant par le foyer F ;
• un rayon passant par le centre de la sphère C est réfléchi sur lui-même ;
• un rayon passant par le sommet S du miroir est réfléchi avec le même angle par rapport à l'axe optique ;
• avec les hypothèses de Gauss (petits angles), tout rayon passant par B passe par son image B', soit réellement si B est devant le miroir, soit virtuellement si B est derrière le miroir.

Généralités

Distance focale : ${\displaystyle f={\frac {\overline {SC}}{2}}}$ où S est le sommet du miroir sphérique et C son centre^[1]. Autrement dit, la distance focale d'un miroir sphérique est la moitié de son rayon de courbure

Grandissement : ${\displaystyle \gamma ={\frac {\overline {A'B'}}{\overline {AB}}}}$.

Lois de Descartes

Relations de conjugaison

Avec origine au sommet'

Pour tout point A sur l'axe du miroir dont l'image est A' (qui est aussi sur l'axe) on peut écrire la relation de conjugaison^[2] :

${\displaystyle {\frac {1}{\overline {SA'}}}+{\frac {1}{\overline {SA}}}={\frac {2}{\overline {SC}}}}$.

On rappelle que ${\displaystyle \scriptstyle {\overline {SA'}}}$ est la mesure algébrique de ${\displaystyle \scriptstyle SA'}$.

Avec origine au centre

Pour tout point A sur l'axe du miroir dont l'image est A' (qui est aussi sur l'axe) on peut écrire la relation de conjugaison^[2] :

${\displaystyle {\frac {1}{\overline {CA'}}}+{\frac {1}{\overline {CA}}}={\frac {2}{\overline {CS}}}}$.

Grandissement

Dans le cas du miroir sphérique on obtient :

${\displaystyle \gamma ={\frac {\overline {A'B'}}{\overline {AB}}}}$ = ${\displaystyle -{\frac {\overline {SA'}}{\overline {SA}}}}$ = ${\displaystyle {\frac {\overline {CA'}}{\overline {CA}}}}$,

où C est le centre du rayon de courbure se trouvant sur l'axe optique.

Formules de Newton

Le grandissement peut aussi être exprimé :

${\displaystyle \gamma ={\frac {\overline {FA'}}{-f}}={\frac {-f}{\overline {FA}}}}$.

D'où la formule de Newton par un produit en croix^[2] :

${\displaystyle {\overline {FA}}}$ x ${\displaystyle {\overline {FA'}}=f.f}$

Miroir concave/convexe

• Miroir convexe, ou « miroir de sorcière » : la surface réfléchissante est du côté opposé du centre de la sphère, la réflexion se fait vers l’extérieur de la sphère.
• Miroir concave : la surface réfléchissante est du même côté que le centre de la sphère, la réflexion se fait vers l'intérieur de la sphère.

• 
  Miroir convexe : si l'objet est réel, l'image est plus petite
• 
  Miroir concave : l'image est agrandie
• 
  Miroir concave : l'image est plus petite et inversée

Utilisation des miroirs sphériques

Projecteur sans contre-miroir (haut), et avec un contre-miroir sphérique (bas).

• Miroir sphérique en dehors des conditions de Gauss : réflecteur dans vidéoprojecteur
• Miroir sphérique dans les conditions de Gauss : télescope

Autres usages courants^[3] :

• miroir convexe :
  • vue panoramique : certains rétroviseurs, miroir de sécurité dans les carrefours dangereux ou à la sortie des parking ;
  • miroir secondaire de certains télescopes : télescope Schmidt-Cassegrain ;
• miroir concave :
  • miroir primaire de certains télescopes : chambre de Schmidt ;
  • miroir de beauté ;
  • contre-miroir des projecteurs.
  • miroir grossissant^[4]

Notes et références

1. Tamer Becherrawy, Optique géométrique : cours et exercices corrigés, Bruxelles, De Boeck Supérieur, 2005, 402 p. (ISBN 2-8041-4912-9, lire en ligne), p. 80
2. Dictionnaire de physique, par Mr Richard Taillet, Mr Pascal Febvre, Mr Loïc Villain sur Google Livres
3. Richard Taillet, "Optique géométrique: MémentoSciences, Ce qu’il faut vraiment retenir ! Premier cycle universitaire – Prépas", De Boeck Supérieur, 2008
4. « Comment fonctionne un miroir grossissant ? », sur Miroir Zoom (consulté le 30 décembre 2020)

Liens externes

Sur les autres projets Wikimedia :

• Sphères réfléchissantes, sur Wikimedia Commons

• Portail de l’optique