Loading AI tools
De Wikipédia, l'encyclopédie libre
L'hypothèse ergodique, ou hypothèse d'ergodicité, est une hypothèse fondamentale de la physique statistique selon laquelle, à l'équilibre, la valeur moyenne d'une grandeur calculée de manière statistique est égale à la moyenne d'un très grand nombre de mesures prises dans le temps. La première valeur est celle que permet de calculer la physique statistique, la seconde est proche de ce qu'on peut expérimentalement mesurer. L'hypothèse ergodique est donc fondamentale pour un bon rapprochement entre la théorie et l'expérience.
L'hypothèse est formulée initialement par Ludwig Boltzmann en 1871 pour les besoins de sa théorie cinétique des gaz. Elle s'applique alors aux systèmes composés d'un très grand nombre de particules.
Un système pour lequel l'hypothèse ergodique est vérifiée est qualifié de système ergodique. Dans la plupart des cas, il est très difficile de démontrer rigoureusement qu'un système est ergodique ou non. L'analyse mathématique de ce problème a donné naissance à la théorie ergodique, qui précise la nature mathématique de l'hypothèse et donne des résultats sur ses conditions de validité. Mais l'hypothèse ergodique reste souvent une simple hypothèse, jugée vraisemblable a posteriori quand elle permet de faire des prédictions correctes. En ce sens, elle constitue un point faible de la physique statistique.
L'hypothèse d'ergodicité intervient également en traitement du signal, où elle consiste à admettre que l'évolution d'un signal aléatoire au cours du temps apporte la même information qu'un ensemble de réalisations. Elle est importante dans l'étude des chaînes de Markov, les processus stationnaires et pour l'apprentissage automatique.
D'une façon intuitive, et pour prendre l'exemple d'un gaz, les milliards de particules qui le constituent peuvent être considérées comme des copies les unes des autres ayant toutes le même comportement aléatoire. Elles prennent chacune des valeurs aléatoires, probablement différentes, de position et de vitesse à un instant donné. La vitesse moyenne des particules peut se calculer en sommant les vitesses de toutes les particules à un instant donné. Cependant, on peut calculer également une moyenne en considérant une seule particule mais en mesurant ses vitesses à différents instants. L'hypothèse d'ergodicité revient à dire que les deux méthodes sont équivalentes.
On peut également penser à une forêt d'une seule espèce et s'intéresser à la croissance d'un arbre en fonction du temps : l'hypothèse ergodique revient à considérer qu'il est similaire d'observer la forêt à un instant donné, ou un arbre tout au long de sa vie pour en connaître l'évolution (par exemple relever le diamètre du tronc en fonction du temps ou mesurer tous les diamètres de la forêt et le reporter en fonction de l'âge de l'arbre).
L'hypothèse ergodique est née avec la théorie cinétique des gaz et la physique statistique dans la seconde moitié du XIXe siècle. Elle fut formulée initialement par Ludwig Boltzmann en 1871[1], ainsi que par Maxwell[2].
Le nom « hypothèse ergodique » ne fut introduit qu'en 1911 par Paul Ehrenfest et Tatiana Afanassieva dans leur célèbre article de revue sur les fondements de la physique statistique[3]. Il est construit à partir des termes grecs εργος, qui signifie « travail », et οδος, pour « chemin ». Boltzmann utilisait pour sa part dès 1884 un mot voisin, « ergoden », mais il donnait à ce mot un sens assez différent[4].
Soit un système à degrés de liberté décrits à l'instant par :
À chaque instant, les coordonnées définissent un point dans l'espace des phases . Ce point représente l'état du système à cet instant .
On considère de plus que le système est à l'équilibre, c'est-à-dire que ses propriétés sont invariantes dans le temps. Un tel système satisfait toujours à la conservation de l'énergie qui s'écrit :
de telle sorte que sa dynamique est toujours restreinte à une hypersurface à dimensions. On supposera dans la suite que le système hamiltonien considéré est invariant par translation dans le temps et qu'il ne possède pas d'autre constante du mouvement que l'énergie[5].
L'évolution dynamique du système selon les équations canoniques de Hamilton à partir d'une condition initiale engendre le flot hamiltonien , c'est-à-dire le groupe continu à un paramètre tel que :
La succession des positions dans l'espace des phases est une courbe continue, appelée orbite.
À une grandeur physique mesurable correspond une fonction sur l'espace des phases qui à chaque point, correspondant à un état du système, associe une valeur. On notera cette fonction. Il existe deux valeurs moyennes distinctes pour cette grandeur. On peut faire une moyenne temporelle en faisant la moyenne d'une série de mesures effectuées sur un temps suffisamment long. Mathématiquement, on la représente par la limite (si elle existe) :
Cette valeur moyenne dépend a priori de la condition initiale .
On peut également définir la moyenne d'ensemble de , ou moyenne microcanonique, par :
La moyenne d'ensemble et la moyenne temporelle n'ont a priori pas de raison d'être égales. L'hypothèse ergodique consiste à supposer qu'elles le sont.
L'évolution du système dans le temps est déterminé par le flot hamiltonien, c'est-à-dire l'application . Cette application sera dite ergodique pour une mesure donnée si et seulement si tout ensemble mesurable invariant sous est de mesure nulle, ou de complémentaire de mesure nulle.
Le théorème de Birkhoff montre alors que lorsque l'application est ergodique, moyenne spatiale et moyenne temporelle sont effectivement égales presque partout.
Le théorème de Birkhoff présenté ci-dessus permet de formuler l'hypothèse ergodique non plus comme une égalité de moyenne, mais en fonction des propriétés du flot hamiltonien , c'est-à-dire de l'évolution du point représentatif du système dans l'espace des phases.
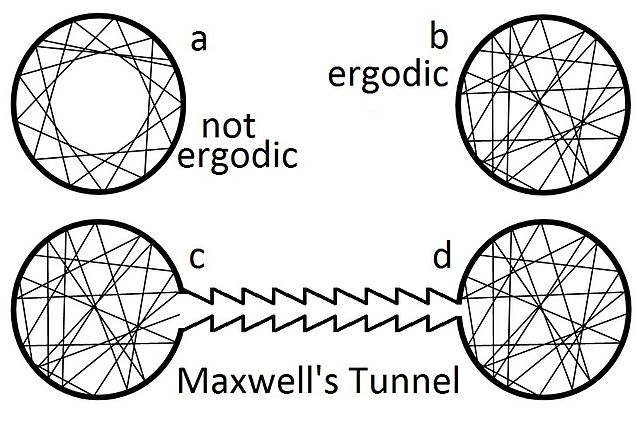
On peut alors distinguer deux hypothèses ergodiques distinctes. Un système hamiltonien invariant par translation dans le temps est dit ergodique au sens fort si le point représentatif de ce système passe au cours du temps par chaque point de l'hypersurface d'énergie constante. Un système hamiltonien invariant par translation dans le temps est dit ergodique au sens faible si le point représentatif de ce système passe au cours du temps aussi près que l'on veut de chaque point de l'hypersurface d'énergie constante.
Boltzmann et Maxwell utilisèrent dans leurs travaux les deux énoncés de façon indifférenciée[6]. La non-équivalence mathématique des deux hypothèses ergodiques précédentes n'a été reconnue explicitement qu'en 1910 par Paul Hertz[7].
Utilisant les résultats de la théorie des ensembles de Cantor d'une part, et de la théorie de la mesure de Lebesgue d'autre part, les deux mathématiciens Plancherel et Rosenthal ont démontré indépendamment le théorème suivant[8] :
En revanche, il a été démontré depuis que certains systèmes pouvaient être ergodiques au sens faible ; voir l'article Théorie ergodique.
En dépit des importants progrès réalisés en théorie ergodique et en théorie du chaos, l'utilisation de l'hypothèse ergodique pour justifier l'utilisation de l'ensemble microcanonique en mécanique statistique reste à ce jour controversée[9].
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.