Loading AI tools
En infographie, la géométrie de construction de solides (CSG en anglais : "Constructive Solid Geometry") est une branche de la modélisation des solides (ou modélisation tridimensionnelle).
Cet article est une ébauche concernant l’informatique.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Pour les articles homonymes, voir CSG.
Cette technique de modélisation géométrique concerne la représentation d'un objet solide comme combinaison d'objets solides simples (exemple : cylindre, sphère, cône, tore, etc.) à l'aide d'opérateurs géométriques booléens (exemple : union, intersection, soustraction).
La modélisation géométrique des solides procède de 2 méthodes :
- la CSG (dite aussi "modélisation solide" ou "modélisation volumique"),
- la B-Rep ("Boundary Representation" dite aussi "modélisation surfacique").
On applique des opérations booléennes et des transformations géométriques.
Transformations géométriques
Ce sont les transformations géométriques classiques :
Opérations booléennes
| Union (ou addition) | Différence (ou soustraction) | Intersection |
|---|---|---|
 |
 |
 |
| L'assemblage des deux objets. | La soustraction d'un objet de l'autre. | La partie commune aux deux objets. |
Union (ou addition)
Le résultat est l'assemblage des deux objets. Il y a parfois la possibilité de réaliser cette opération sur plus de deux objets.
Différence (ou soustraction)
Le résultat est le premier objet moins la partie commune avec le second. Avec certains logiciels (POV-Ray par exemple), il est possible d'inverser un objet (ce qui revient à faire la soustraction inverse)…
Intersection
Le résultat est la partie commune aux deux objets.
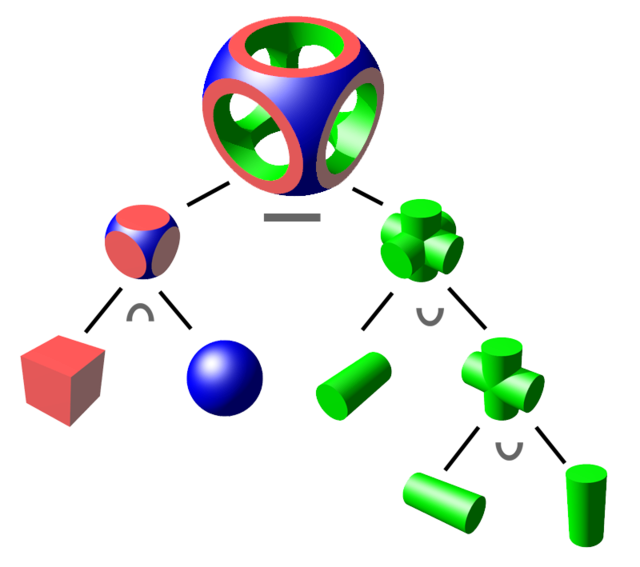
- : intersection
- : union
- : différence
La géométrie de construction de solides est stockée sous une forme arborescente (arbre) qui décrit : l'opération et les éléments manipulés. L'utilisation d'arbre permet de faire très facilement des modifications.
Avantages
Description spatiale
De par sa nature mathématique, les volumes complexes décrits par cette technique ont des frontières parfaites et non approchées comme par les techniques à base de polygones par exemple. Ainsi, les bords d'une sphère seront parfaits, quel que soit le niveau de détail choisi.
Optimisation des calculs
La géométrie de construction de solides permet d'accélérer les calculs qui peuvent se baser sur des volumes plutôt que sur les polygones.
- Cette méthode de modélisation est assez adaptée au lancer de rayon car ce dernier travaille principalement par intersection de demi-droites avec des volumes mathématiques, et permet des calculs allégés. Par exemple, l'intersection d'une droite avec une sphère est plus facile qu'avec un ensemble de polygones approchant la forme de la sphère.
- De façon plus étendue, la géométrie de construction de solides accélère tous les calculs de projection : clipping, culling, ombres... Il est en effet plus rapide de projeter un polygone formé par les arêtes d'un solide que de projeter les polygones du solide.
- Les calculs de collision entre deux solides convexes sont très rapides, il suffit de tester si au moins un des deux a un point inclus dans l'autre.
- Le calcul d'éventuelles réflexions ou réfractions à l'intérieur des volumes est facilité car on connaît précisément les équations décrivant la surface du volume, en particulier la normale et la tangente
Inconvénients
- La liberté de modélisation est restreinte par les possibilités de créer le volume désiré par un ensemble d'opérations. De plus les formes présentes dans le monde réel sont peu ou pas géométriques et même un ballon n'est pas parfaitement sphérique lorsqu'il est posé sur le sol.
- On peut facilement arriver à des hiérarchies d'opérations très complexes qui vont alourdir les calculs de rendu.
- Le nombre de primitives disponibles va directement influer sur l'algorithme de rendu car ce dernier doit savoir les prendre toutes en compte ce qui peut alourdir son écriture.
Pour le rendu temps réel rapide, on compile la géométrie de construction de solides dans un format qui retient le résultat des opérations booléennes. L'espace est alors statique.
Articles connexes
- Opération ensembliste
- Ensemblist, un jeu qui utilise la Géométrie de Construction de Solides.
Liens externes
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
