Loading AI tools
livre de Galilée De Wikipédia, l'encyclopédie libre
Les Discours et démonstrations mathématiques concernant deux sciences nouvelles (en italien : Discorsi e dimostrazioni matematiche intorno a due nuove scienze), publiés en 1638, sont le dernier livre et le testament scientifique de Galilée couvrant une grande partie de ses travaux en physique des trente années précédentes. Le livre est écrit en partie en italien et en partie en latin.
| Discours et démonstrations mathématiques concernant deux sciences nouvelles | |
.png)
| |
| Auteur | Galilée |
|---|---|
| Date de parution | 1638 |
modifier  |
|
Il s'agit d'un livre fondateur de la science moderne. Les deux nouvelles sciences abordées par l'auteur sont celle de la résistance des matériaux et la mécanique. Le livre est connu pour son analyse mathématique de la chute des corps.
Les Discours sont écrits dans un style semblable à celui du Dialogue sur les deux grands systèmes du monde, où trois hommes (Simplicio, Sagredo, et Salviati) discutent et débattent des diverses questions que Galilée cherche à résoudre. Il y a cependant un changement notable, puisque Simplicio n'est plus un esprit simple, obstiné et aristotélicien, comme son nom l'implique. Ses arguments sont représentatifs des croyances initiales de Galilée lui-même, tandis que Sagredo représente sa période intermédiaire, et que Salvati propose les modèles de Galilée les plus récents.
Après son Dialogue sur les deux grands systèmes du monde, l'Inquisition romaine interdit toutes les publications de Galilée, passées et futures[1]. À la suite de l'échec de ses tentatives pour publier les Discours concernant deux sciences nouvelles en France, Allemagne et Pologne, il est publié par Louis Elzevir qui travaille à Leyde, en Hollande-du-Sud, où le mandat de l'Inquisition a moins d'importance[2]. Au départ, Fulgenzio Micanzio, théologien officiel de la république de Venise, avait offert à Galilée de publier le nouveau livre à Venise, mais il avait mis en avant que publier les Discours à Venise pourrait causer à Galilée des problèmes inutiles ; c'est pourquoi le livre est finalement publié en Hollande. Galilée ne semble avoir subi aucun préjudice de la part de l'Inquisition à cause de cette publication, puisqu'en 1639 le livre atteint les rayons des librairies de Rome, et que tous les exemplaires (une cinquantaine) se sont rapidement vendus[3].
Le livre est organisé en quatre journées, chacun d'elles aborde différents domaines de la physique[4]. Galilée dédie les Discours au comte François de Noailles[5].
Dans la Première Journée, Galilée aborde des sujets traités dans la Physique d'Aristote ainsi que la mécanique de l'école aristotélicienne. Ce chapitre constitue aussi une introduction à la discussion des deux sciences nouvelles. La ressemblance entre les sujets traités, les hypothèses avancées, le style et les sources fournissent à Galilée l'ossature de sa Première Journée. Celle-ci présente les protagonistes du dialogue : Salviati, Sagredo, et Simplicio, le même que dans le Dialogue. Ces trois personnages représentent tous Galilée à différentes étapes de sa vie, Simplicio dans sa jeunesse tandis que Salviati est son homologue le plus proche.
La Deuxième Journée aborde la question de la résistance des matériaux.
Les Troisième et Quatrième Journées concernent la science du mouvement. La Troisième discute du mouvement uniforme et naturellement accéléré, le problème de la vitesse terminale ayant été traité dans la Première Journée. La Quatrième discute le mouvement des projectiles.
Dans les Discours, le mouvement uniforme est défini comme un mouvement qui, sur des périodes de temps égales quelconques, couvre une distance égale. Avec l'usage du quantificateur « quelconques », l'uniformité est introduite et définie plus explicitement que dans ses définitions plus anciennes[6].
Galilée a commencé une Journée supplémentaire sur la force de percussion, mais n'est jamais parvenu à l'achever de façon satisfaisante à ses yeux. Cette section est souvent citée dans les quatre premières Journées. Elle n'est finalement apparue que dans l'édition de 1718 des œuvres de Galilée[7]. Elle est fréquemment désignée comme « Sixième Journée » suivant la numérotation de l'édition de 1898[8]. Dans cette Journée additionnelle, Simplicio est remplacé par Paolo Aproino, un ancien disciple et assistant de Galilée à Padoue[9].
Les numéros de pages en tête des paragraphes renvoient à l'édition de 1898[8], aujourd'hui adoptée comme princeps, et se retrouvent dans la traduction anglaise de Crew et Drake, ainsi que celle en français de Maurice Clavelin.
[50] Discussions préliminaires. Sagredo (supposé représenter Galilée plus jeune) ne comprend pas pourquoi, au sujet des machines, il ne faut pas raisonner des petites aux grandes, car « les démonstrations mécaniques ont leur fondement dans la géométrie où ni la grandeur ni la petitesse ne confèrent aux cercles, aux cylindres, aux cônes et à toute autre figure solide, tantôt certaines propriétés et tantôt certaines autres[10]. » Salviati (qui parle pour Galilée) dit que l'opinion commune est fausse. L'échelle a son importance : un cheval qui tombe d'une hauteur de 3 ou 4 coudées se rompt les os, tandis qu'un chat tombant de deux fois sa hauteur non, pas plus qu'une sauterelle chutant du haut d'une tour.
[56] Le premier exemple est celui d'une corde de chanvre qui est constituée de petites fibres liées ensemble, de la même façon qu'une corde enroulée autour d'un cabestan a beaucoup plus de résistance. La deuxième expérience concerne deux plaques planes et polies : on peut facilement les faire glisser l'une contre l'autre, mais il est difficile de les séparer en soulevant celle du dessus. Comment expliquer que celle de dessous colle à la première ? L'explication aristotélicienne de ce phénomène, qui rejette l'existence du vide, est mise en question. Salviati évoque alors une expérience destinée à déterminer si l'eau peut se dilater ou bien s'il faut supposer l'existence du vide. Sagredo rapporte qu'il a observé qu'une pompe aspirante était incapable de soulever l'eau au-delà d'une hauteur de dix-huit coudées. Pour Salviati, cette hauteur correspond à la valeur de la résistance au vide. La discussion passe ensuite au sujet de la résistance d'un fil de cuivre et à la question de savoir s'il existe de minuscules espaces vides à l'intérieur du métal ou s'il existe une autre explication à sa solidité.
[68] L'idée d'une infinité de petits vides conduit les interlocuteurs à réfléchir aux concepts d'infini et de continu. Ils se demandent si le continu peut être composé d'une infinité d'éléments indivisibles. Pour Salviati, comparer des grandeurs infinies n'a pas de sens : on ne peut pas dire qu'un infini est « plus grand » ou « plus petit » qu'un autre. Un continu, comme une ligne, est constitué de parties douées de grandeur. Ces parties ne sont ni en nombre fini, ni en nombre infini. La distinction entre infini en puissance et infini en acte est évoquée. Salviati en arrive à l'affirmation que « si un nombre peut être dit infini, ce doit être l'unité. » Une construction géométrique lui permet de démontrer que, dans le passage du fini à l'infini, il y a changement de nature.
[85] Ce changement de nature correspond à celui que l'on observe quand on réduit un solide en poussière, ou entre un solide et un liquide. La différence entre une fine poudre et un liquide conduit à s'interroger sur l'action de la lumière et comment la concentration des rayons du soleil peut faire fondre le métal. Salviati en déduit que la lumière a un mouvement, et il décrit une tentative (infructueuse) pour établir sa vitesse.
[106] Aristotle récuse les philosophes qui ont recours à l'hypothèse du vide parce que sinon, selon eux, le mouvement serait impossible. Il avance que le mouvement, dans le vide, serait instantané, ce qui est récusé par l'observation. Il croit que les corps tombent à une vitesse proportionnelle à leur masse. Mais Salviati doute qu'il ait pu en faire l'expérience. Il met au défi quiconque de déceler une différence entre la durée de la chute d'un boulet d'artillerie et celle d'une balle de mousquet. Il l'affirme : dans un milieu dépourvu de résistance (le vide), tous les corps - un morceau de laine comme une bille de plomb - tomberaient à la même vitesse. Selon lui, le corps le plus pesant ne tombe pas plus vite. Le mouvement dans l'air nous en donne une idée. Dans l'air, dont la ténuité le rapproche du vide, un corps pesant et un plus léger tombent à des vitesses dont la différence est imperceptible. Cette différence n'est pas due à la différence des poids, mais à la résistance du milieu. Salviati propose une expérience pour mesurer le poids de l'air.
[128] Salviati reconnaît que la mesure de la vitesse d'une chute est est rendu difficile par les faibles intervalles de temps qu'elle implique. C'est pourquoi sa première solution a consisté à utiliser des pendules de la même longueur mais avec des poids en plomb ou en liège. La période d'oscillation est identique, même quand le poids est lancé avec plus d'amplitude pour compenser le fait qu'il s'arrête rapidement.
[139] Cela conduit à une discussion sur la vibration des cordes d'un instrument de musique et sur le phénomène de vibration par sympathie. Galilée suggère que la hauteur du son est proportionnelle à la longueur de la corde, mais aussi à son poids (plutôt qu'à sa grosseur) et à sa tension.
[151] La discussion revient sur la résistance à la rupture. La question est ramenée à la théorie du levier. Salviati prouve qu'une balance est en équilibre non seulement si ses bras sont de longueurs égales, mais même si ses bras sont inégaux, pourvu que leurs poids soient inversement proportionnels à leur distance du fulcrum (pivot). Ensuite il montre que le moment d'un poids suspendu à un levier soutenu à l'une de ses extrémités est proportionnel au carré de la longueur. La résistance à la fracture de leviers de différentes tailles et épaisseurs, selon qu'ils sont soutenus à l'une de leurs extrémités ou les deux, est démontrée.
[169] Galilée établit que l'art comme la nature rencontrent des limites dans la solidité de leurs œuvres. Ainsi, la taille du squelette d'un animal doit être en proportion de la taille de l'animal. Il détermine la longueur d'un cylindre qui se brisera sous son propre poids. Il prouve que le meilleur endroit pour briser un bâton en le frappant sur son genou est son milieu. Il montre qu'une poutre est plus solide à mesure que le poids qui s'exerce sur elle est éloigné de son milieu.
[178] Il démontre que la meilleure forme pour une poutre soutenue à une extrémité et supportant un poids à l'autre est parabolique. Il montre aussi qu'un cylindre creux est plus robuste et solide qu'un cylindre plein du même poids.
[191] Galilée commence par définir le mouvement uniforme (régulier) et montre la relation entre la vitesse, le temps et la distance. [197] Il définit alors le mouvement uniformément accéléré par l'augmentation de la vitesse dans des intervalles de temps identiques (« en des temps égaux quelconques se produisent des additions égales de vitesse[11] »). Le mouvement continuellement accéléré est celui qui concerne la chute des corps. Un corps qui tombe commence très lentement. Galilée entreprend de montrer que sa vélocité s'accroît simplement en proportion du temps, non de la distance.
[208] Il démontre que la distance parcourue dans le mouvement naturellement accéléré est proportionnelle au carré des temps. Il décrit une expérience dans laquelle un boulet descend le long d'un plan incliné en bois de 12 coudées de longueur (environ 5,50 mètres) dont une extrémité est élevée d'une ou deux coudées. L'expérience est répétée, en mesurant le temps par l'évaluation précise du poids de l'eau écoulée d'un mince tuyau du fond d'une grande cruche d'eau. Il affirme avoir été capable par ce moyen de vérifier le mouvement uniformément accéléré. Il montre alors que, quelle que soit l'inclinaison du plan, le carré du temps pris par la chute du haut d'une hauteur donnée est proportionnel à la distance inclinée.
[221] Il examine ensuite la descente le long des cordes d'un cercle, montrant que la durée de la chute depuis le vertex (sommet) est la même pour toutes les cordes, et diverses autres combinaisons de plans. Il donne une solution erronée au problème de la courbe brachistochrone, prétendant prouver que l'arc du cercle est la descente la plus rapide. Il étudie 16 problèmes et leurs solutions.
[268] Le mouvement d'un projectile consiste en la combinaison d'un mouvement horizontal uniforme et d'un mouvement vertical naturellement accéléré qui produit une courbe parabolique. Il montre en détail comment construire les paraboles correspondant à diverses situations et donne les tables pour l'altitude et la portée en fonction de l'angle du projectile.
[274] La résistance de l'air se manifeste de deux manières : en affectant davantage les corps les moins denses et en offrant une plus grande résistance aux plus rapides. Un boulet de plomb tombe légèrement plus vite qu'une boule de bois, mais la différence avec une boule de pierre est négligeable. Cependant la vitesse ne va pas en augmentant indéfiniment : elle atteint un maximum. Bien que l'effet de la résistance de l'air soit faible pour de petites vitesses, il est plus important si l'on considère, par exemple, un boulet tiré par un canon.
[292] L'effet de l'impact d'un projectile sur une cible est réduit si cette dernière est libre de son mouvement. L'effet est maximum si le choc a lieu à angle droit et si la cible offre une résistance. L'auteur démontre ce qui est connu par expérience : lors du tir d'un boulet de canon, on obtient la portée la plus grande avec une élévation de 45 °.
[310] Une corde ou une chaîne tendue n'est jamais de niveau mais tend toujours à adopter la forme d'une parabole (chaînette).
[325] La percussion dans le cas d'un pieu qu'on enfonce dans le sol. Explication de la force du marteau.
[336] La vitesse de chute le long de plans inclinés. Le principe d'inertie est supposé par Galilée, mais pas explicitement formulé[12].
Beaucoup des savants contemporains de Galilée, tels que Gassendi, mettent en question la méthodologie qu'il a développée pour conceptualiser sa loi de la chute des corps. On a tantôt considéré que son épistémologie suivait l'exemple de la pensée de Platon, tantôt qu'elle adoptait une méthode empirique hypothético-déductive. C'est la première thèse que défend Alexandre Koyré : selon lui les expériences décrites par Galilée sont des abstractions, des « expériences en pensée » que Galilée n'a pas toujours pu réellement effectuer. Mais Thomas Settle a entrepris avec succès de reproduire certaines des expériences de Galilée pour montrer qu'elles étaient probantes[13]. On aurait donc sous-estimé la part expérimentale dans la méthode de Galilée. On considère aujourd'hui que sa méthode est ex suppositione, c'est-à-dire qu'elle consiste à connaître le comment et le pourquoi des événements passés afin de déterminer les conditions pour reproduire des effets similaires dans le futur. La méthodologie galiléenne serait donc le reflet de l'épistémologie d'Aristote et d'Archimède. Dans une lettre au cardinal Bellarmine en 1615, Galilée distingue ses arguments et ceux de Copernic comme des suppositions « naturelles », par opposition aux suppositions « fictives » qui ne sont introduites que pour les besoins du calcul et pour « sauver les phénomènes », comme les hypothèses de Ptolémée sur les excentriques et les équants[14].
Les premiers écrits de Galilée, désignés sous le titre de Juvenilia, ou écrits de jeunesse, sont considérés comme sa première tentative pour créer des notes pour son cours « hypothèses sur le mouvement céleste » quand il enseignait à l'université de Padoue. Ces notes reflètent les principes méthodologiques de ses contemporains au Collegio, mais elles comportent aussi un « contexte aristotélicien avec une forte connotation thomiste »[15]. Il semble que ces premiers articles ont encouragé Galilée à appliquer la preuve démonstrative afin de valider ses découvertes sur le mouvement.
La découverte du folio 116v apporte la preuve d'expériences qui n'avaient jusque-là pas été rapportées et démontrent la méthode de calcul de Galilée pour la loi de la chute des corps[16].
Sa méthode expérimentale a été validée par des chercheurs tels que James MacLachlan, Stillman Drake, R.H. Taylor, qui ont refait ses expériences et ainsi prouvé qu'il ne s'agissait pas seulement d'expériences imaginaires, comme le croyait Alexandre Koyré.
Galilée croit que la science peut être acquise par le raisonnement, et renforcée par l'observation et l'expérimentation. On peut donc affirmer que Galilée est un rationaliste, mais aussi un empiriste. Ni purement platonicien, ni purement empiriste, il suit une démarche aristotélico-archimédienne ex suppositione.
Les deux sciences nouvelles mentionnées dans le titre sont celle de la résistance des matériaux et celle du mouvement (les ancêtres de la science des matériaux et de la cinématique)[17]. Dans le titre du livre, « mécanique » et « mouvement » sont séparés[18], car à l'époque de Galilée, la « mécanique » ne désignait que la statique et la résistance des matériaux[19].
La discussion commence par une démonstration de la raison pour laquelle une structure plus grande structuré exactement avec les mêmes proportions qu'une plus petite est nécessairement plus fragile, connue sous le nom de loi des carrés et des cubes. Plus tard dans la discussion ce principe est appliqué à la taille requise pour le squelette d'un gros animal, peut-être le premier résultat quantitatif en biologie, précédant l'œuvre de J. B. S. Haldane On Being the Right Size (en), and other essays (1926)[20].
Galilée est le premier à exprimer explicitement l'accélération constante d'un corps en chute, qu'il a pu évaluer en utilisant un plan incliné destiné à ralentir la chute pour la rendre mesurable.
Dans les Discours, Galilée (Salviati parle pour lui) dit avoir utilisé « un chevron de bois , long d'environ 12 coudées, large d'une demi-coudée et épais de trois doigts » comme rampe où il a creusé une rigole bien polie et rectiligne pour étudier des boulets (« une boule de bronze très dure »)[21]. Il garnit le plan incliné « d'une feuille de parchemin pour le rendre aussi glissant que possible ». Il incline la rampe selon différents angles, et ralentit assez l'accélération pour qu'il puisse mesurer le temps écoulé. Il laisse la boule parcourir une distance déterminée et se sert d'une horloge à eau pour mesurer le temps pris pour parcourir la distance[21]. Cette horloge est
« un grand seau rempli d'eau que nous attachions assez haut ; par un orifice étroit pratiqué dans son fond s'échappait un mince filet d'eau que l'on recueillait dans un petit récipient, tout le temps que la boule descendait dans le canal. Les quantités d'eau ainsi recueillies étaient à chaque fois pesées à l'aide d'une balance très sensible... »
Tandis qu'Aristote avait observé que les objets les plus lourds tombaient plus vite que les plus légers, dans les Deux nouvelles sciences, Galilée postule que ce fait est dû non pas aux forces inhérentes agissant sur les objets les plus lourds, mais aux forces contraires dues à la résistance de l'air et à la friction. Pour le prouver, il mène des expériences où il se sert d'un plan légèrement incliné, assez poli pour éliminer autant de friction que possible, sur lequel il fait rouler des boules de différents poids. Ainsi, il parvient à prouver de façon empirique que la matière accélère verticalement à un taux constant, indépendamment de la masse, en raison des effets de la gravité[16],[22].
L'expérience inédite rapportée dans le folio 116v met à l'épreuve le taux constant d'accélération dans la chute des corps en raison de la gravité[16]. Cette expérience consiste à laisser tomber un boulet de diverses hauteurs sur un déflecteur de façon à transformer son mouvement vertical en mouvement horizontal. Les données issues des expériences avec le plan incliné sont exploitées pour calculer le mouvement horizontal attendu. Cependant, des écarts apparaissent dans les résultats de l'expérience : les distances horizontales observées sont en désaccord avec les distances prévues par le calcul pour un taux constant d'accélération. Galilée attribue ces écarts à la résistance de l'air dans l'expérience inédite, et à la friction dans celle du plan incliné. Ces écarts forcent Galilée à affirmer que le postulat ne tient que dans des « conditions idéales », c'est-à-dire en l'absence de friction et de résistance de l'air.
La physique aristotélicienne affirme que la Terre est immobile puisque les humains ne sont pas en mesure de percevoir les effets de son mouvement[23]. L'opinion populaire la justifie par l'exemple d'un archer qui lance une flèche à la verticale. Si la Terre bougeait, argumente Aristote, la flèche devrait retomber en un autre point que celui d'où elle a été tirée. Galilée réfute cet argument dans son Dialogue sur les deux grands systèmes du monde. Il donne l'exemple de marins à bord d'un navire en mer. Le navire est bien sûr en mouvement, mais les marins sont incapables de percevoir ce mouvement. Si un marin laisse tomber un objet pesant du haut du mât, l'objet tombera au pied du mât, et non en arrière, bien que le navire avance[24].
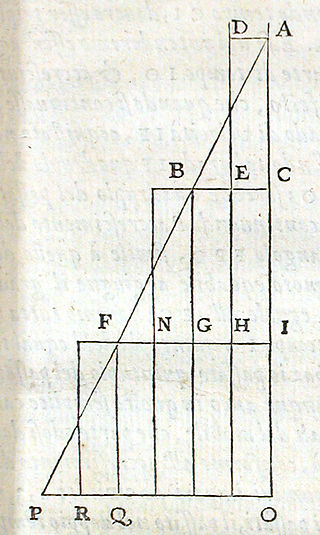
L'un des arguments de Galilée concernant la chute des corps est celui qui décrit la relativité des mouvements, expliquant que, dans les circonstances convenables, un mouvement peut se superposer à un autre sans qu'ils s'affectent l'un l'autre[25]. Dans les Deux sciences nouvelles, Galilée fait valoir cet argument qui, sous une forme plus explicite, deviendra la première loi de Newton, la loi de l'inertie.
Il pose la question de ce qui arrive à un boulet qu'on laisse tomber du haut du mât ou à la flèche, tirée du pont d'un navire à la verticale. Selon la physique d'Aristote, le boulet lâché devrait atterrir à la poupe du navire, du fait qu'il tombe à la verticale pendant que ce dernier avance. De même, la flèche tirée au-dessus de la tête de l'archer ne devrait pas retomber au point d'où elle a été lancée si le navire se déplace. Galilée propose l'idée qu'il y a deux mouvements indépendants en jeu. L'un est le mouvement vertical accéléré dû à la gravité tandis que l'autre est le mouvement horizontal uniforme dû au mouvement du navire qui continue d'influencer la trajectoire du boulet en vertu du principe d'inertie. De la combinaison de ces deux mouvements résulte une courbe parabolique. L'observateur ne peut identifier cette courbe parce que lui et le boulet partagent le mouvement horizontal qui leur est communiqué par le navire, ce qui signifie que seul le mouvement perpendiculaire vertical lui est perceptible. Étrangement, personne n'a expérimenté cette théorie malgré les conditions simples qu'elle requiert pour être probante, jusqu'à ce que Pierre Gassendi en publie les résultats dans ses lettres intitulées De Motu Impresso a Motore Translato (1642)[26].
Le livre comporte aussi une réflexion sur l'infini. Galilée examine l'exemple des nombres et de leurs carrés. Il commence par noter que :
« Si je me demande combien il y a de racines, on ne peut nier qu'il y en a autant que de nombres, puisque tout nombre est la racine de quelque carré ; cela étant, il faudra donc dire qu'il y a autant de nombres carrés qu'il y a de nombres. »Galilée, Discours concernant deux sciences nouvelles (trad. Clavelin), p. 31
En langage moderne, il y a bijection entre les éléments de l'ensemble des entiers positifs N et l'ensemble des carrés S, et S est un sous-ensemble de densité arithmétique zéro. Mais il relève aussitôt ce qui semble une contradiction :
« et pourtant nous disions au début qu'il y a beaucoup plus de nombres que de carrés, étant donné que la plus grande partie des nombres ne sont pas des carrés. À quoi s'ajoute le fait que la proportion des carrés diminue toujours davantage quand on passe à des nombres plus élevés. »(ibidem)
Il résout la contradiction en rejetant la possibilité de comparer des nombres infinis entre eux aussi bien qu'avec des nombres finis :
« La seule issue possible est de dire que l'ensemble des nombres est infini, que le nombre des carrés est infini, et le nombre de leurs racines pareillement ; que le total des nombres carrés n'est pas inférieur à l'ensemble des nombres, ni celui-ci supérieur à celui-là, et, finalement, que les attributs « égal », « plus grand » et « plus petit » n'ont pas de sens pour les quantités infinies, mais seulement pour les quantités finies. »
Cette conclusion, que l'attribution de dimensions à des ensembles infinis doit être jugée impossible, en raison des résultats contradictoires obtenus par l'opinion commune quand elle essaie de le faire, est une solution cohérente, mais moins puissante, que les méthodes utilisées dans les mathématiques modernes. La résolution du problème peut être généralisée en examinant la première définition par Galilée de ce qu'il entend par des ensembles de dimensions égales, à savoir la possibilité de créer entre eux une correspondance biunivoque[27]. Cela fournit un moyen de comparer les tailles d’ensembles infinis exempt de résultats contradictoires.
Ces problèmes concernant l'infini découlent de l'examen du paradoxe de la roue d'Aristote (Problèmes mécaniques, 855)[28]. Si deux cercles concentriques mais de rayons différents roulent chacun le long d'une ligne, et si le plus grand ne glisse pas, alors il est clair que le plus petit doit glisser. En effet, la petite roue parcourt une distance plus grande que sa propre circonférence. Les deux cercles, de rayons différents, auraient la même circonférence, ce qui est absurde[29]. Galilée tente de résoudre le problème de la correspondance point par point de deux lignes de longueurs inégales en analysant la nature du continu et de l'infini[30]. Pour ce faire, il examine, pour clarifier la question, le cas d'un hexagone puis de polygones à 100.00 côtés ou n côtés[31]. Il suppose l'existence d'une infinité de vides sans grandeur intercalés entre les points dont la ligne est constituée[32]. Il conclut finalement que « la ligne parcourue par les côtés infiniment nombreux et continûment disposés du grand cercle est égale en longueur à la ligne parcourue par les côtés infiniment nombreux du petit cercle, à condition que l'on intercale entre ceux-ci autant d'espaces vides »[33]. Cette solution n'est pas jugée satisfaisante aujourd'hui, où l'on considère que le continu n'est pas constitué d'une infinité de points, mais d'une infinité de points possibles[34].
« La contribution des Deux sciences nouvelles à la physique est si grande que les historiens ont longtemps prétendu que ce livre anticipait les lois du mouvement de Newton. »-- Stephen Hawking. On the Shoulders of Giants, p. 397.
« (Galileo is ) the father of modern physics and in fact of the whole of modern natural science »-- Albert Einstein. « On the method of theoretical physics » in Philosophy of Science, 1933
Une partie des Deux sciences nouvelles est purement mathématique, comme le souligne le mathématicien Alfréd Rényi, pour qui il s'agit du livre sur les mathématiques le plus significatif depuis 2.000 ans : les mathématiques grecques ne traitent pas du mouvement, et par conséquent elles n'ont jamais formulé des lois du mouvement, même si Archimède a développé le calcul des dérivées et l'intégration. Les Deux sciences nouvelles ouvrent la voie au traitement mathématique de la physique en considérant pour la première fois le mouvement d'un point de vue mathématique. Le mathématicien grec Zénon a conçu ses paradoxes pour prouver que le mouvement ne pouvait être traité mathématiquement, et que toute tentative en ce sens conduisait à une contradiction. Aristote renforce cette croyance en affirmant que les mathématiques ne pouvaient parler que d'objets abstraits et immuables. Galilée se sert de la méthode même des Grecs pour prouver qu'il est possible de traiter le mouvement en termes mathématiques. Son idée est de séparer, parmi les paradoxes de Zénon, ceux qui concernent l'infini. Il réalise ce programme en plusieurs étapes. Premièrement, il établit que la suite infinie S des carrés 1, 4, 9, 16... contient autant d'éléments que la suite N des entiers positifs (une infinité) ; ce point est aujourd'hui connu sous le nom de paradoxe de Galilée (en). Ensuite, en utilisant une géométrie de type grec, il montre qu'un bref segment de droite contient autant de points qu'un segment plus long. Il en arrive à formuler le principe général qu'un ensemble infini plus petit peut comporter exactement autant de points qu'un ensemble infini plus grand, dans lequel il est contenu. Il devient alors clair que les paradoxes de Zénon sur le mouvement proviennent de sa conception des quantités infinies. Rényi dit que, ayant levé cet obstacle vieux de 2.000 ans, Galilée en vient à présenter ses lois mathématiques du mouvement, anticipant celles de Newton[35].
Pierre Gassendi défend les opinions de Galilée dans son livre, De Motu Impresso a Motore Translato. Dans l'article d'Howard Jones Gassendi's Defence of Galileo: The Politics of Discretion, Jones dit que Gassendi a fait preuve d'une claire compréhension des arguments de Galilée et de leurs implications vis-à-vis des objections contre le mouvement de la Terre[36].
La loi sur la chute des corps a été publiée par Galilée en 1638. Mais au XXe siècle des auteurs sont contesté la réalité des expériences de Galilée. EN particulier, l'historien français des sciences Alexandre Koyré fonde ses doutes sur le fait que les expériences décrites dans les Deux sciences nouvelles pour déterminer la loi d'accélération des corps en chute nécessitent une mesure du temps précise qui paraît impossible avec la technologie des années 1600. Selon Koyré, la loi a été pensée de façon purement déductive, et l'expérience décrite n'est qu'une expérience de pensée.
Mais en fait, l'horloge à eau de Galilée fournit une mesure suffisamment précise pour confirmer ses conjectures. Des recherches ultérieures, en effet, ont validé ses expériences. Les expériences sur la chute des corps (en fait des boulets qui roulent) a été reproduite en suivant la méthode décrite par Galilée, et la précision des résultats est cohérente avec les comptes-rendus de Galilée[37]. Les recherches récentes sur les œuvres inédites de Galilée (folio 152r de 1604) montrent clairement la réalité de ses expérimentations et même indiquent les résultats précis qui ont conduit à la formulation de la loi du carré des temps[38].
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
