Loading AI tools
De Wikipédia, l'encyclopédie libre
En mathématiques, et plus spécialement dans les applications de la théorie des catégories, un diagramme commutatif est un diagramme d'objets et de morphismes tels que, si l'on suit à travers le diagramme un chemin d'un objet à un autre, le résultat par composition des morphismes ne dépend que de l'objet de départ et de l'objet d'arrivée.
Le premier théorème d'isomorphisme est un triangle commutatif comme suit :
Puisque f = h ∘ φ, le diagramme de gauche est commutatif ; et puisque φ = k ∘ f, il en est de même pour le diagramme de droite.
Sur le diagramme de gauche, il est possible d'aller de G à im f par deux chemins différents : soit directement grâce à l'application f, soit par composition des applications h et φ. De même, le diagramme de droite est commutatif, puisqu'on peut aller de G à G/ ker f soit directement par l'application φ, soit par la composition de k par f en passant par l'objet intermédiaire im f.
De la même manière, le carré ci-dessus est commutatif si y ∘ w = z ∘ x.
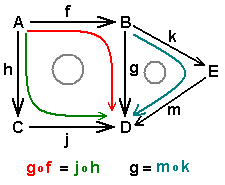
La commutativité est aisément compréhensible pour un polygone avec un nombre fini de côtés (y compris seulement 1 ou 2), et un diagramme est commutatif si tout sous-diagramme polygonal est commutatif.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
