Loading AI tools
L’axiome d'Euclide, dit également cinquième postulat d’Euclide, est dû au savant grec Euclide (IVe siècle av. J.-C.). C'est un axiome relatif à la géométrie du plan.
Cet article est une ébauche concernant les mathématiques.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
La nécessité de cet axiome a constitué la question la plus lancinante de toute l'histoire de la géométrie, et il a fallu plus de deux millénaires de débats ininterrompus pour que la communauté scientifique reconnaisse l'impossibilité de le réduire au statut de simple théorème.
L'énoncé original est exprimé dans le livre I des Éléments d'Euclide sous la forme suivante[1],[2] :
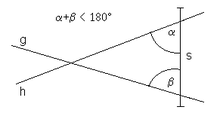
« Si une droite tombant sur deux droites fait les angles intérieurs du même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits. »
(voir figure).
En langage moderne, cela pourrait donner :
« Si une droite coupe deux autres droites en déterminant deux angles internes dont la somme est différente de deux angles droits, alors les deux droites se coupent dans le demi-plan pour lequel la somme est inférieure à deux angles droits. »
Euclide
Euclide a présenté cette propriété comme une "demande" c'est à dire un postulat.
Il est assez vraisemblable que[réf. souhaitée] lui-même doutait de savoir si son affirmation était ou non démontrable. Les raisons pour le penser sont autant le choix de la propriété dont l'énoncé est plutôt celui d'un « théorème indémontrable », que le fait qu'Euclide établit les 28 premières propositions de ses Éléments sans recourir à son fameux axiome[3], comme s'il avait voulu inviter ses lecteurs à s'en passer, et les inciter par là à le démontrer[réf. souhaitée].
Essais de démonstrations et propositions équivalentes
De fait, pendant plus de deux millénaires, bien des géomètres ont pensé que cette propriété devait découler logiquement des autres postulats. Ils ont donc tenté de prouver l'axiome d'Euclide. Parmi les plus illustres de ces savants on citera :
|
Comme la démonstration de l'axiome requerrait de le ramener à des évidences, d'autres énoncés plus ou moins équivalents au postulat d'Euclide ont résulté des meilleures de ces tentatives de démonstration. Les variantes connues sont assez nombreuses. Les plus célèbres sont probablement :
- « Par un point donné, on peut mener une et une seule parallèle à une droite donnée ». Cette forme de l'axiome d'Euclide est due au mathématicien Antique Proclus. Elle est connue sous le nom de postulat des parallèles, et sous le nom de postulat de Playfair dans le monde anglo-saxon.
- « Il existe des quadrilatères à quatre angles droits. »
- « Il existe des triangles dont la somme des angles est égale à deux droits. » (Legendre)
- « Il existe des triangles semblables de toutes les tailles. » (John Wallis)
- « Par trois points non alignés d'un plan, on peut toujours mener un cercle et un seul. » (Farkas Bolyai)
- …
Ces propositions sont considérées comme « grossièrement équivalentes » à l'axiome des parallèles. Par équivalentes, il faut comprendre que moyennant des conventions de vocabulaire adaptées, ces axiomes, vrais en géométrie euclidienne, ne le sont ni en géométrie hyperbolique, ni en géométrie elliptique[11].
Par exemple, les deux axiomes suivants ne sont pas équivalents à l'axiome d'Euclide :
- « Si deux droites non parallèles sont prolongées à l'infini, elles s'écartent indéfiniment. »
- « Il existe des droites parallèles. »
En effet, ces axiomes vrais en géométrie euclidienne le sont également en géométrie hyperbolique. Ils ne permettent donc pas de démontrer l'axiome d'Euclide. Cependant, ils sont apparentés à l'axiome d'Euclide, car ils sont faux en géométrie sphérique.
Géométries non euclidiennes
Au XIXe siècle, avec les recherches de Lobatchevski, Bolyai, Gauss, Riemann, Beltrami, Klein et Poincaré, on a pu trouver d'autres géométries possibles et non contradictoires en conservant les axiomes de la géométrie d'Euclide[12] à l'exception du cinquième postulat ; ces nouvelles géométries sont appelées non euclidiennes. L'histoire de cette découverte est un épisode fascinant de l'histoire de la géométrie ; elle est retracée dans ses grandes lignes à l'article « Géométrie non euclidienne »[13].
On trouve deux manières différentes de pratiquer la géométrie sans l'axiome des parallèles.
Dans la première, la somme des angles d'un triangle est supérieure à 180° : on l'appelle géométrie elliptique (dont la géométrie sphérique est un modèle) ; dans l'autre, elle est inférieure à 180° : c'est la géométrie hyperbolique ou géométrie de Lobatchevski. Par exemple, en modifiant le cinquième axiome ainsi : « Par un point extérieur à une droite, on peut faire passer une infinité de droites parallèles à cette droite », on obtient la géométrie hyperbolique.
Dans les géométries non euclidiennes, la plupart des résultats métriques, c’est-à-dire ceux concernant les distances et les angles (par exemple le théorème de Pythagore) ne sont plus vrais.
Résistances
Le postulat d'Euclide est lié à une certaine perception immédiate de l'espace. Y renoncer n'est probablement pas facile. Dans Les Fous littéraires[14], André Blavier cite 13 ouvrages parus entre 1862 et 1932 écrits par ceux que l'auteur appelle du terme plus général de « quadrateurs » qui pensent démontrer le postulat d'Euclide.
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
