Algorithme de Prim

L'algorithme de Prim est un algorithme glouton qui calcule un arbre couvrant minimal dans un graphe connexe pondéré et non orienté. En d'autres termes, cet algorithme trouve un sous-ensemble d'arêtes formant un arbre sur l'ensemble des sommets du graphe initial et tel que la somme des poids de ces arêtes soit minimale. Si le graphe n'est pas connexe, alors l'algorithme détermine un arbre couvrant minimal d'une composante connexe du graphe.

Arbre couvrant de poids minimum

Historique

L'algorithme a été développé en 1930 par le mathématicien tchèque Vojtech Jarnik^[1], puis a été redécouvert et republié par Robert C. Prim^[2] et Edsger W. Dijkstra en 1959. Ainsi, il est parfois appelé DJP algorithm^[3], Jarník's algorithm^[4], Prim–Jarník algorithm^[5], ou Prim–Dijkstra algorithm^[6].

Principe

L'algorithme^[7] consiste à faire croître un arbre depuis un sommet. On part d'un sous-ensemble contenant un sommet unique. À chaque itération, on agrandit ce sous-ensemble en prenant l'arête incidente à ce sous-ensemble de coût minimum. En effet, si l'on prend une arête dont les deux extrémités appartiennent déjà à l'arbre, l'ajout de cette arête créerait un deuxième chemin entre les deux sommets dans l'arbre en cours de construction et le résultat contiendrait un cycle.

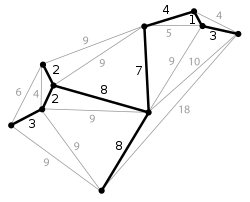
Exemple

Exécution de l'algorithme de Prim depuis le sommet A.

À droite, on donne un exemple d'exécution de l'algorithme de Prim.

Pseudo-code

Le pseudo-code^[7] de l'algorithme de Prim est similaire à celui de l'algorithme de Dijkstra et utilise le type abstrait file de priorité.

 fonction prim(G, s)
       pour tout sommet t
              cout[t] := +∞
              pred[t] := null
       cout[s] := 0
       F := file de priorité contenant les sommets de G avec cout[.] comme priorité 
       tant que F ≠ vide
            t := F.defiler
            pour toute arête t--u avec u appartenant à F
                si cout[u] >= poids de l'arête entre les sommets t et u
                       pred[u] := t
                       cout[u] := poids de l'arête entre les sommets t et u
                       F.notifierDiminution(u)
                        
       retourner pred

Au début tous les sommets sont dans la file de priorité. La priorité est donnée par cout[.]. Autrement dit, le sommet possédant la plus faible valeur dans le tableau cout[.] sortira en premier de la file. On retire un à un les sommets de la file de priorité. Le tableau pred[.] contient le prédécesseur d'un sommet dans l'arbre en construction. L'algorithme retourne le tableau pred qui représente l'arbre couvrant de poids minimum.

Complexité

Soit ${\displaystyle G=(S,A)}$ le graphe en entrée, où ${\displaystyle |S|}$ est le nombre de sommets dans le graphe et ${\displaystyle |A|}$ est le nombre d'arcs dans le graphe, on effectue ${\displaystyle |S|}$ opérations défiler-min et ${\displaystyle 2\times |A|}$ opérations réduire-priorité donc ${\displaystyle C_{Prim}\in O(|S|\times C_{defilermin}(S)+|A|\times C_{reduirepriorite}(S)+C_{iterergraphe}(S,A))}$.

Le cout de l'itération du graphe ${\displaystyle C_{iterergraphe}(S,A)}$ est le cout total d'itération des voisins de la boucle interne durant l'exécution de l'algorithme. Pour une implémentation d'un graphe sous forme de matrice d'adjacence, ${\displaystyle C_{iterergraphe}(S,A)\in O(|S|^{2})}$ alors que lors d'une implémentation sous forme de liste d'adjacence, ${\displaystyle C_{iterergraphe}(S,A)\in O(|A|)}$.^[8]

Si l'on regarde la complexité de ces deux opérations avec trois possibilités de files de priorités, on obtient les complexités ci-dessous :

File de priorité	Graphe	${\displaystyle C_{defilermin}}$	${\displaystyle C_{reduirepriorite}}$	${\displaystyle C_{Prim}}$
Liste (informatique)	matrice d'adjacence	${\displaystyle O(S)}$	${\displaystyle O(1)}$	${\displaystyle O(|S|^{2})}$
tas min binaire	liste d'adjacence	${\displaystyle O(log(S))}$[9]	${\displaystyle O(log(S))}$[9]	${\displaystyle O(|A|\log |S|)}$
tas de Fibonacci	liste d'adjacence	${\displaystyle O(log(S))}$ am.	${\displaystyle O(1)}$ am.[9]	${\displaystyle O(|A|+|S|\log |S|)}$[source insuffisante]

am. : Complexité amortie

Preuve de correction

Soit G un graphe connexe pondéré. À chaque itération de l'algorithme de Prim, on trouve une arête qui connecte un sommet dans un sous-graphe à un sommet à l'extérieur du sous-graphe. Puisque G est connexe, il y aura toujours un chemin vers tous les sommets. La sortie Y de l'algorithme de Prim est un arbre, parce que chaque sommet (sauf le premier) est relié à exactement un prédécesseur.

Soit A_i l'ensemble des i premières arêtes ajoutées à l'arbre Y par l'algorithme de Prim et A₀ = {}. On va montrer que, pour chacun des A_i, il existe un arbre couvrant minimal de G contenant A_i. Alors il existera un arbre couvrant minimum qui contiendra Y et sera donc Y. Pour ce faire, supposons qu'il existe un premier ensemble A_k tel qu'aucun arbre couvrant minimal ne contient A_k. Soit e l'arête qui appartient à A_k mais n'appartient pas à A_k-1, soit Y₁ un arbre couvrant minimum du graphe G qui contient toutes les arêtes d' A_k-1 et soit S l'ensemble de sommets reliés par les arêtes d' A_k-1. Une extrémité de l'arête e est dans l'ensemble S et l'autre n'est pas. Puisque l'arbre Y₁ est un arbre couvrant du graphe G, il y a un chemin dans l'arbre Y₁ joignant les deux extrémités de e. Lorsque l'on se déplace le long du chemin, on doit rencontrer une arête f qui joint un sommet de S à un sommet qui n'est pas dans l'ensemble S. Alors, à l'itération où l'arête e a été ajoutée à l'arbre Y, l'arête f pourrait aussi avoir été ajoutée et elle serait ajoutée au lieu de e si son poids était moins que celui de e, et puisque l'arête f n'a pas été ajoutée, nous concluons que

${\displaystyle w(f)\geq w(e).}$

Soit Y₂ l'arbre obtenu en enlevant l'arête f et en ajoutant l'arête e à l'arbre Y₁. Il est facile de montrer que l'arbre Y₂ est un arbre couvrant et le poids total de ses arêtes n'est pas supérieur à celui de l'arbre Y₁ et que Y₂ contient toutes les arêtes d' A_k. On arrive à une contradiction, car on a supposé qu'il existe un ensemble A_k tel qu'aucun arbre couvrant de poids minimum ne contient les arêtes d' A_k. C'est donc que l'hypothèse faite est fausse.