From Wikipedia, the free encyclopedia
Kenttäviiva on vektorikenttään liittyvä käyrä, jonka tangentti käyrän jokaisessa pisteessä on kentän suuntainen. Kenttäviivoja käytetään havainnollistamaan vektorikenttiä, joita on vaikea kuvata ilman niitä. Samoin kuin leveys- ja pituuspiirit pallon pinnalla tai korkeuskäyrät topografikartalla, eivät kenttäviivatkaan ole todellisia fysikaalisia viivoja, jotka todella olisivat kentässä tietyissä kohdissa, vaan ne ovat vain kentän havainnollistamiseksi keksitty apuväline.


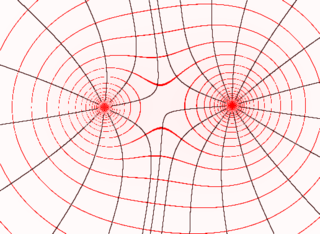
Kenttäviivat ovat kaikkialla kohtisuorassa kentän ekvipotentiaaleja eli sellaisia pintoja vastaan, joilla kentän potentiaali on vakio.[1]
Vektorikenttä on avaruuden jokaisessa pisteessä tietyn suuntainen, paitsi missä se on nolla. Vektorikentän kenttäviiva voidaan muodostaa piirtämällä jostakin kentän pisteestä alkava viiva, joka jokaisessa kohdassaan on kentän suuntainen. Täsmällisemmin sanottuna käyrän tangentti on joka kohdassa saman suuntainen kuin kenttä kyseessä pisteessä.[2] Saman kentän kenttäviivat eivät leikkaa toisiaan.
Täydellinen geometrinen kuvaus vektorikentän kaikista kenttäviivoista riittää täysin määrittämään vektorikentän suunnan kaikkialla. Jotta kenttäviivat ilmaisisivat myös vektorikentän suuruuden, valitaan piirrettäväksi vain tietty määrä kenttäviivoja siten, että näitä viivoja on eri alueilla sitä tiheämmässä, mitä suurempi itseisarvoltaan vektorikenttä missäkin on. Toisin sanoen kenttää vastaan kohtisuorien kenttäviivojen lukumäärä pinta-alayksikköä kohti on suoraan verrannollinen vektorikentän suuruuteen tällä alueella.[2]
Divergenssilauseen mukaan kentät alkavat alueilta, joissa vektorikentän divergenssi on positiivinen ja päättyvät alueille, joissa sen divergenssi on negatiivinen. Edellisiä sanotaan kentän lähteiksi, jälkimmäisiä nieluiksi. Fysiikassa kenttäviivojen piirtäminen on kätevää varsinkin tapauksissa, joissa mahdollisilla lähteillä ja nieluilla on jokin selvä fysikaalinen merkitys (toisin kuin esimerkiksi radiaalisen harmonisen oskillaattorin tapauksessa).
Gaussin lain mukaan sähkökentän lähteitä ovat positiiviset, nieluja negatiiviset varaukset ja vain ne. Näin ollen kenttäviivat alkavat positiivisista ja päättyvät negatiivisiin varauksiin[2], elleivät ne ulotu jommassakummassa päässään äärettömän kauas. Sitä vastoin sellaisen sähkökentän kenttäviivat, joka syntyy Faradayn induktiolain mukaisesti muuttuvassa magneettikentässä syntyy myös sähkökenttä, mutta tässä tapauksessa sen kenttäviivat voivat olla myös suljettuja käyriä tai ulottua molemmissa päissään äärettömän kauas.
Jotta kenttäviivat, joiden niiden tiheys on verrannollinen kentän suuruuteen, kuvaisivat tilannetta oikein, on kuitenkin otettava huomioon kaikki kolme ulottuvuutta. Ajatellaan esimerkkinä yksittäisen eristetyn pistevarauksen sähkökenttää. Tässä tapauksessa kenttäviivat ovat suoria viivoja, joita lähtee varauksesta kaikkiin suuntiin kolmiulotteisessa avaruudessa. Tämä merkitsee, että niiden tiheys on kääntäen verrannollinen varauksesta mitatun etäisyyden neliöön (suoraan verrannollinen lausekkeeseen ), samoin kuin Coulombin lain mukaan onkin sähkökentän voimakkuuden laita. Jos kuitenkin kenttäviivoja piirretään vain kaksiulotteiselle tasolle, niiden kaksiulotteinen tiheys tuleekin kääntäen verrannolliseksi etäisyyteen, mikä ei vastaa sähkökentän voimakkuutta eri kohdissa.[3]
Ehkä tunnetuin esimerkki vektorikentästä on magneettikenttä, jota usein havainnollistetaan magneettia ympäröivien kenttäviivojen avulla.
Gaussin lain magneettikentällä ei ole lähteitä eikä nieluja, minkä vuoksi kenttäviivoilla ei ole alkua eikä loppua. Ne ovat joko suljettuja käyriä tai ulottuvat molemmissa päissään äärettömän kauas. Toisinaan ne piirretään alkamaan magneetin pohjoisnavasta ja päättymään sen etelänapaan, mutta itse asiassa niiden on ajateltava jatkuvan myös magneetin sisällä sen etelänavasta pohjoisnapaan, jolloin niistä muodostuu joko suljettuja tai molemmissa päissään äärettömyyteen ulottuvia käyriä.
Gravitaatiokentällä ei ole lähteitä, mutta sillä on nielu kaikkien massallisten kappaleiden kohdalla. Näin ollen gravitaatiokentän kenttäviivoilla ei ole alkukohtaa vaan ne tulevat äärettömän kaukaa, mutta ne päättyvät massoihin.
Myös virtaavaa ainetta, nestettä tai kaasua, voidaan kuvata kenttäviivoilla. Tällöin niiden suunta kussakin paikassa esittää virtauksen suuntaa, tiheys taas sen nopeutta.
Kenttäviivojen kulku osoittaa myös, onko kenttä pyörteetön tai lähteetön.
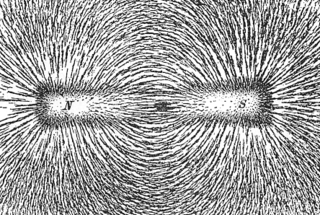
Vaikka kenttäviivat ovat oikeastaan vain matemaattinen konstruktio, joissakin tilanteissa niillä on selvä fysikaalinen merkitys. Virtausmekaniikassa nopeuskentän kenttäviivat, virtausviivat, osoittavat virtaavan aineen hiukkasten liikeratoja. Plasmafysiikassa elektronit tai ionit, jota ovat samalla kenttäviivalla, vuorovaikuttavat keskenään voimakkaasti, kun taas eri kenttäviivoilla olevat hiukkaset eivät yleensä vuorovaikuta. Tässä suhteessa niiden käyttäytyminen muodostaa rautajyvästen käyttäytymistä magneettikentässä.
Jos magneetin ympärille levitetään rautajauhetta, sen jyväset kääntyvät ferromagneettisuutensa vuoksi kentän suuntaisiksi. Samalla ne magnetoituvat, jolloin kunkin jyväsen pohjoisnapa vetää puoleensa toisen kohtion etelänapaa. Tällä tavoin jyväsistä muodostuu ketjuja, jotka johtavat alkuperäisen magneetin toisesta navasta toiseen ja kulkevat sitä ympäröivän kentän kenttäviivojen mukaisesti.[6] Koska jyvästen oma magneettisuus muuttaa kenttää, niiden muodostamat viivat vastaavat kuitenkin vain likipitäen alkuperäistä magneettikenttää. Lisäksi todelliset magneettikentät ovat jatkuvia, eikä niissä ole erillisiä viivoja.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.