klassinen matemaattinen ongelma graafiteorian ja topologian alalta From Wikipedia, the free encyclopedia
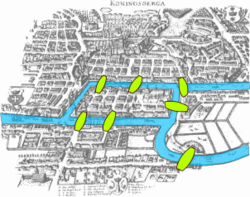
Königsbergin siltaongelma on klassinen matemaattinen ongelma graafiteorian ja topologian alalta. Königsbergin eli nykyisen Kaliningradin läpi virtaa Pregolja-joki (saks. Pregel), jonka keskellä on kaksi saarta. 1700-luvulla saaret oli yhdistetty toisiinsa ja mantereeseen seitsemällä sillalla (kuva oikealla). Ongelmana oli keksiä sellainen reitti, jota kulkemalla voitaisiin ylittää jokainen silta täsmälleen yhden kerran ja päätyä takaisin lähtöpisteeseen. Leonhard Euler todisti vuonna 1736, ettei tällaista reittiä ole olemassa.
Kuultuaan Königsbergin siltaongelmasta sveitsiläinen matemaatikko Leonhard Euler päätti ratkaista sen. Hän aloitti abstrahoimalla Königsbergin kartan poistaen ensin ylimääräiset piirteet siten, että jäljelle jäävään kuvaan oli merkitty vain maamassat, niitä erottava vesi ja niiden väliset sillat. Seuraavaksi hän korvasi maamassat pisteillä ja niitä yhdistävät sillat viivoilla saaden tulokseksi alla kuvatun verkon, jota graafiteorian käsitteillä kutsutaan graafiksi. Pisteitä taas kutsutaan solmuiksi ja viivoja kaariksi.
Graafin muotoa voidaan muokata vapaasti ilman, että graafi itse muuttuu, kunhan solmujen väliset yhteydet pysyvät samoina. Ei ole merkitystä, ovatko kaaret suoria vai käyriä, tai millä puolella toista solmua jokin solmu sijaitsee. Solmun asteluku on siihen ulottuvien kaarien lukumäärä.
Euler todisti, että graafiin on mahdollista piirtää polku, Eulerin kehä, joka kulkee graafin jokaisen kaaren kautta täsmälleen kerran palaten alkusolmuun, jos ja vain jos graafissa ei ole yhtään solmua, jonka asteluku on pariton. Königsbergin silloista muodostuvassa graafissa on kolme solmua, joiden asteluku on kolme, ja yksi solmu, jonka asteluku on viisi, yhteensä siis neljä asteeltaan paritonta solmua, joten polkua ei Königsbergin tapauksessa ole mahdollista piirtää.
Ongelma voidaan muuntaa sellaiseksi, että etsitään polkua, joka ylittää jokaisen sillan kerran, mutta jonka alku- ja loppupiste ei välttämättä ole sama. Tällaista polkua kutsutaan Eulerin poluksi; se on olemassa, jos ja vain jos graafissa on täsmälleen kaksi (tai ei yhtään) solmua, joiden asteluku on pariton siten, että nämä kaksi solmua ovat polun alku- ja loppusolmu. Königsbergin siltojen kohdalla tämäkään ehto ei toteudu.
Eulerin ratkaisua Königsbergin siltaongelmaan pidetään matematiikan historian ensimmäisenä teoreemana, joka koskee nykyisin graafiteoriana tunnettua matematiikan alaa. Tätä puolestaan pidetään nykyään yleisesti kombinatoriikan haarana (kombinatorisia ongelmia oli toki tutkittu jo paljon aikaisemmin).
Lisäksi Eulerin huomio siitä, että ongelman ratkaisemisen avain olivat siltojen määrä ja loppupisteet (eikä niiden täsmällinen sijainti), enteili topologian kehittymistä. Königsbergin kartan ja siitä johdetun kaavakuvan välinen ero havainnollistaa, että esineiden jäykkä muoto ei sinänsä ole merkityksellinen topologiassa.
Eulerin aikaisista Königsbergin silloista on jäljellä enää kaksi. Kaksi tuhoutui toisen maailmansodan ilmapommituksissa. Yksi purettiin jo vuonna 1935 uuden sillan tieltä, ja kaksi muuta on myöhemmin purettu ja tilalle rakennettu moderni päätie.[1] Vanhan kaupungin alueella on siis nykyisin vain viisi siltaa.
Näin ollen graafiteorian kannalta nykyisin kahdella solmupisteellä on asteluku 2, kahdella muulla asteluku 3. On siis mahdollista kulkea kaikkien siltojen yli kerran, mutta tällöin reitin on alettava toiselta ja päätyttävä toiselle saarelle. Toisin sanoen Eulerin polku on olemassa, mutta Eulerin kehää ei.[2] Hieman keskikaupungin länsipuolella on kuitenkin myös kuudes silta, joka johtaa suoraan joen toiselta rannalta toiselle.[3] Jos se otetaan huomioon, kaikkien solmupisteiden asteluku on pariton eikä Eulerin polkuakaan ole olemassa.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.