نظریه آشوب

برای دیگر کاربردها، نظریه آشوب (ابهام‌زدایی) و آشوب (ابهام‌زدایی) را ببینید.

نظریه آشوب (به انگلیسی: Chaos Theory)، شاخه‌ای از ریاضیات است که به مطالعه سامانه‌های پویای آشوب‌ناک می‌پردازد؛ سامانه‌هایی که بی‌نظمی آن‌ها، در ظاهر، تصادفی است اما در واقع، از الگوها و قوانین قطعی پیروی می‌کند که به‌شدت به شرایط اولیه حساسند.^[1][2] نظریه آشوب، دانشی میان‌رشته‌ایست که بر اساس آن، سامانه‌های پیچیده به‌ظاهر تصادفی، الگوها، درون‌پیوستگی‌ها، حلقه‌های بازخوردی، تکرار، خودهمانندی، فراکتال‌ها، و خودسازماندهی دارند.^[3] اثر پروانه‌ای، زیربنای نظریه آشوب است، و به توصیف این پدیده می‌پردازد که چگونه تغییرات بسیار کوچک در شرایط اولیه یک سامانه قطعی و غیرخطی، می‌تواند به تغییرات بزرگی در پاسخ سیستم بینجامد؛ یعنی وابستگی حساس به شرایط اولیه.^[4] استعاره‌ای از این رفتار، پروانه‌ای است که در تگزاس بال می‌زند و طوفانی در چین به‌پا می‌کند.^[5]

نموداری از جاذب لورنتس برای${\displaystyle r=28,\sigma =10,b=8/3}$.

پویانمایی از آونگ دو-میله‌ای که در انرژی میانی، رفتار آشوبناک دارد. وقتی شرایط آغازین آونگ کمی متفاوت شوند، مسیر حرکتش بسیار متفاوت خواهد شد. آونگ دو-میله‌ای یکی از ساده‌ترین سامانه‌های دینامیکی با پاسخ آشوب‌ناک است.

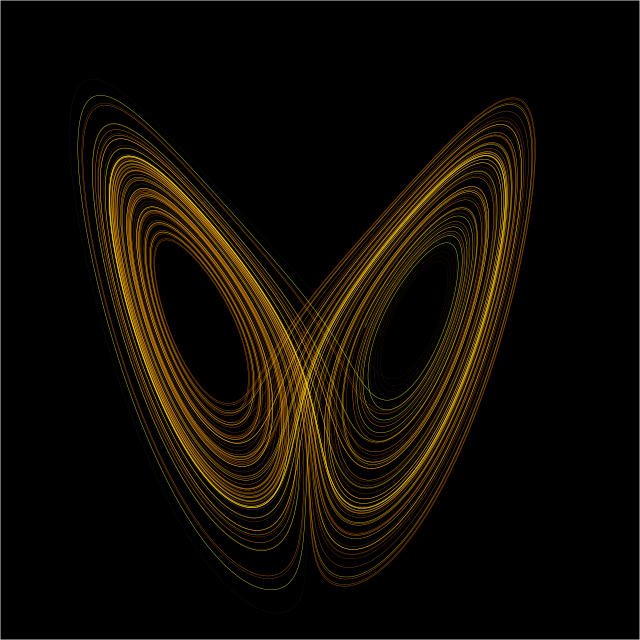
تغییرات کوچک در شرایط اولیه، مانند تغییرات در اثر گرد کردن اعداد در محاسبات، می‌تواند باعث واگرایی گسترده خروجی‌های چنین سامانه‌هایی شده، به‌گونه‌ای که پیش‌بینی بلندمدت رفتارشان را در حالت کلی، غیرممکن می‌سازد.^[6] بااین‌که این‌گونه سامانه‌ها قطعی هستند، ممکن است چنین شود. قطعی بودن به این معناست که رفتار آینده‌شان از سیر تکاملی منحصربه‌فردی پیروی کرده،^[7] کاملاً وابسته به شرایط اولیه بوده، و هیچ اثری از رفتار تصادفی در آن دیده‌نمی‌شود.^[8] به بیانی دیگر، ماهیت قطعی این سامانه‌ها، باعث پیش‌بینی‌پذیری‌شان نمی‌شود.^[9][10] به این رفتار، آشوب قطعی یا تنها، آشوب می‌گویند. این نظریه را ادوارد لورنتس این‌گونه خلاصه کرد:^[11]

آشوب، هنگامی‌ست که حال، آینده را تعیین می‌کند، اما حالِ تقریبی نتواند آینده را تقریبی تعیین کند.

رفتار آشوب‌ناک در بسیاری از سامانه‌های طبیعی دیده‌می‌شود؛ جریان سیالات، بی‌نظمی‌های تپش قلب، آب‌وهوا و اقلیم.^[12][13][7] همچنین این پدیده، در برخی سامانه‌ها با مؤلفه‌های مصنوعی، همچون بازار سهام و ترافیک جاده‌ها نیز خودبه‌خود رخ می‌دهد.^[14][3] این رفتار را می‌توان از راه تحلیل مدل ریاضیاتی، با کمک فنون تحلیلی چون نمودارهای بازگشتی و نگاشت‌های پوانکاره، مطالعه کرد. نظریه آشوب در رشته‌های گوناگونی مانند هواشناسی،^[7] انسان‌شناسی،^[15] جامعه‌شناسی،^[16] علوم محیطی، علوم رایانه، مهندسی، اقتصاد، بوم‌شناسی، مدیریت بحران همه‌گیری جهانی،^[17][18] و فلسفه کاربرد دارد. این نظریه، پایه رشته‌های علمی چون سامانه‌های پویای پیچیده، نظریه مرز آشوب و فرایندهای خودسامانی است.

تاریخچه

معرفی و گسترش نظریه آشوب، مدیون کارهای پوانکاره، ادوارد لورنتس، بِنُوآ ماندِل‌بُرو و میچل فایگن‌باوم است. پوانکاره نخستین کسی بود که ثابت کرد مسئله سه جسم (برای نمونه، خورشید، زمین، ماه) مسئله‌ای آشوب‌ناک و غیرقابل حل است. شاخهٔ دیگر نظریه آشوب که در مکانیک کوانتومی پیش می‌آید، آشوب کوانتومی نام دارد. گفته می‌شود که لاپلاس و خیام، پیش‌از پوانکاره، به آشوب پی برده‌بودند.

نخستین بار، یک هواشناس به‌نام ادوارد لورنتس به مسئله آشوب‌ناکی برخورد. ۱۹۶۰، او روی پیش‌بینی آب‌وهوا کار می‌کرد و روی کامپیوترش ۱۲ معادله برای آن در نظر گرفته‌بود. این معادله‌ها، آب‌وهوا را پیش‌بینی نمی‌کرد، ولی، نظری، پیش‌بینی می‌کرد که هوا چگونه می‌تواند باشد. او می‌خواست دوباره به دنبالهٔ مشخصی برسد. برای صرفه‌جویی در وقت، او به‌جای آغاز از اول دنباله، از وسط آن شروع کرد. عددی را که از بار پیش، از دنباله در دست داشت، وارد سیستم کرد، و کامپیوتر را به حال خود گذاشت تا پردازش کند. یک ساعت بعد که برگشت، دنباله، متفاوت از بار پیش، ادامه یافته‌بود. برخلاف بار پیش، دنباله جدید واگرا می‌شد و نسبت به دنباله اول، کاملاً به‌هم‌ریخته می‌نمود. لورنتس، سرانجام دریافت که مشکل کار کجاست. کامپیوتر، تا ۶ رقم اعشار را ذخیره می‌کرد و او برای این‌که کاغذ کمتری مصرف کند، فقط ۳ رقم اعشار را برای خروجی در نظر گرفته‌بود. در الگوی اولیه، عدد به‌دست‌آمده در اصل، ۵۰۶۱۲۷/۰ بود، ولی او برای بار بعد، فقط ۵۰۶/۰ را وارد کرده‌بود. براساس دانش آن زمان، این دنباله می‌بایست شبیه یا بسیار نزدیک به دنباله اولیه می‌شد. او انتظار داشت، رقم‌های پنجم و ششم مهم نباشند و اثر چندانی روی خروجی نگذارند. اما چنین نبود. لورنز اما آن را نپذیرفت.

این پدیده، به‌عنوان اثر پروانه‌ای شناخته شد. در واقع، تفاوت دو مقدار اولیه آن‌قدر ناچیز است، که انتظار می‌رود به اندازه اثر بال زدن یک پروانه روی وضعیت جوی باشد. مانند این‌که در یک دوره آب‌وهوایی، گردبادی که قرار بود سواحل اندونزی را درنوردد، هیچ‌گاه اتفاق نمی‌افتد. این پدیده، حساسیت زیاد به شرایط اولیه را نشان می‌دهد.

پژوهش‌های متخصصان در مطالعات هواشناسی ادامه یافت تااین‌که ۱۹۹۱، جیمز یورک، نظریه آشوب را به مفهوم «نظم در بی‌نظمی» پیش نهاد. او استاد ریاضی و فیزیک در دانشگاه مریلند و به پدر آشوب مشهور است.

دینامیک آشوبناک

نگاشت تعریف شده با ${\displaystyle x\to 4x(1-x)}$ و ${\displaystyle y\to (x+y){\pmod {1}}}$، حساسیت نسبت به موقعیت آغازین ${\displaystyle x}$ را نمایش می‌دهد. در اینجا، دو سری از مقادیر ${\displaystyle x}$ و ${\displaystyle y}$ که در ابتدا اختلاف اندکی دارند، با گذر زمان، اختلافشان، قابل توجه، بیشتر می‌شود (واگرا شدن).

«آشوب» به‌معنای «نوعی بی‌نظمی» است.^[19][20] البته در نظریه آشوب، این اصطلاح تعریف دقیق‌تری دارد. گرچه آشوب، تعریف ریاضی همگانی ندارد، تعریف رایج را رابرت دِوانی پیش نهاد، که چنین است: یک سامانه دینامیکی، آشوب‌ناک است اگر یکی از سه ویژگی را دارا باشد:^[21]

1. نسبت به شرایط اولیه حساس باشد.
2. از نظر توپولوژیک، متعدی باشد.^{[persian-alpha 1]}
3. مدارهای چگال متناوب داشته‌باشد.

نشان داده‌شده که در برخی موارد، در واقع دو ویژگی ۲ و ۳ هستند که موجب حساسیت به شرایط اولیه می‌شوند.^[22][23] در مسائل زمان‌گسسته، این برای تمام نگاشت‌های پیوسته روی فضاهای متریک صدق می‌کند.^[24] در چنین مواردی، با این که خاصیت «حساسیت نسبت شرایط اولیه» اغلب در عمل مهم است، ولی لازم نیست در تعریف آشوب‌ناکی قید شود.

اگر تنها بازه‌ها در نظر گرفته‌شوند، خاصیت دوم، دو خاصیت دیگر را نتیجه می‌دهد.^[25] تعریف کلی‌تر اما ضعیف‌تری از آشوب، تنها دو خاصیت اول را دربرمی‌گیرد.^[26]

جستارهای وابسته

• بنوا مندلبروت
• اثر پروانه‌ای
• فراکتال

یادداشت‌ها

1. Topologically Transitive

منابع

1. "The Definitive Glossary of Higher Mathematical Jargon — Chaos". Math Vault (به انگلیسی). 2019-08-01. Retrieved 2019-11-24.
2. "chaos theory | Definition & Facts". Encyclopedia Britannica (به انگلیسی). Retrieved 2019-11-24.
3. "What is Chaos Theory? – Fractal Foundation" (به انگلیسی). Retrieved 2019-11-24.
4. Weisstein, Eric W. "Chaos". mathworld.wolfram.com (به انگلیسی). Retrieved 2019-11-24.
5. Boeing, Geoff. "Chaos Theory and the Logistic Map" (به انگلیسی). Retrieved 2020-05-17.
6. Kellert, Stephen H. (1993). In the Wake of Chaos: Unpredictable Order in Dynamical Systems. University of Chicago Press. p. 32. ISBN 978-0-226-42976-2.
7. Bishop, Robert (2017), "Chaos", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2017 ed.), Metaphysics Research Lab, Stanford University, retrieved 2019-11-24
8. (Kellert 1993، ص. 56)
9. (Kellert 1993، ص. 62)
10. Werndl, Charlotte (2009). "What are the New Implications of Chaos for Unpredictability?". The British Journal for the Philosophy of Science. 60 (1): 195–220. arXiv:1310.1576. doi:10.1093/bjps/axn053. S2CID 354849.
11. Danforth, Christopher M. (April 2013). "Chaos in an Atmosphere Hanging on a Wall". Mathematics of Planet Earth 2013. Retrieved 12 June 2018.
12. Lorenz, Edward N. (1963). "Deterministic non-periodic flow". Journal of the Atmospheric Sciences. 20 (2): 130–141. Bibcode:1963JAtS...20..130L. doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2.
13. Ivancevic, Vladimir G.; Tijana T. Ivancevic (2008). Complex nonlinearity: chaos, phase transitions, topology change, and path integrals. Springer. ISBN 978-3-540-79356-4.
14. Safonov, Leonid A.; Tomer, Elad; Strygin, Vadim V.; Ashkenazy, Yosef; Havlin, Shlomo (2002). "Multifractal chaotic attractors in a system of delay-differential equations modeling road traffic". Chaos: An Interdisciplinary Journal of Nonlinear Science. 12 (4): 1006–1014. Bibcode:2002Chaos..12.1006S. doi:10.1063/1.1507903. ISSN 1054-1500. PMID 12779624.
15. Mosko M.S. , Damon F.H. (Eds.) (2005). On the order of chaos. Social anthropology and the science of chaos. Oxford: Berghahn Books.
16. Hubler, A (1989). "Adaptive control of chaotic systems". Swiss Physical Society. Helvetica Physica Acta 62: 339–342.
17. Piotrowski, Chris. "Covid-19 Pandemic and Chaos Theory: Applications based on a Bibliometric Analysis". researchgate.net. Retrieved 2020-05-13.
18. Weinberger, David (2019). Everyday Chaos - Technology, Complexity, and How We're Thriving in a New World of Possibility. Harvard Business Review Press. ISBN 978-1-63369-396-8.
19. Definition of chaos at Wiktionary;
20. "Definition of chaos | Dictionary.com". www.dictionary.com (به انگلیسی). Retrieved 2019-11-24.
21. Hasselblatt, Boris; Anatole Katok (2003). A First Course in Dynamics: With a Panorama of Recent Developments. Cambridge University Press. ISBN 978-0-521-58750-1.
22. Elaydi, Saber N. (1999). Discrete Chaos. Chapman & Hall/CRC. p. 117. ISBN 978-1-58488-002-8.
23. Basener, William F. (2006). Topology and its applications. Wiley. p. 42. ISBN 978-0-471-68755-9.
24. Banks; Brooks; Cairns; Davis; Stacey (1992). "On Devaney's definition of chaos". The American Mathematical Monthly. 99 (4): 332–334. doi:10.1080/00029890.1992.11995856.
25. Vellekoop, Michel; Berglund, Raoul (April 1994). "On Intervals, Transitivity = Chaos". The American Mathematical Monthly. 101 (4): 353–5. doi:10.2307/2975629. JSTOR 2975629.
26. Medio, Alfredo; Lines, Marji (2001). Nonlinear Dynamics: A Primer. Cambridge University Press. p. 165. ISBN 978-0-521-55874-7.

برای مطالعه بیشتر

مقالات

• Sharkovskii, A.N. (1964). "Co-existence of cycles of a continuous mapping of the line into itself". Ukrainian Math. J. 16: 61–71.
• Li, T.Y.; Yorke, J.A. (1975). "Period Three Implies Chaos" (PDF). American Mathematical Monthly. 82 (10): 985–92. Bibcode:1975AmMM...82..985L. CiteSeerX 10.1.1.329.5038. doi:10.2307/2318254. JSTOR 2318254. Archived from the original (PDF) on 29 December 2009. Retrieved 21 April 2021.
• Alemansour, Hamed; Miandoab, Ehsan Maani; Pishkenari, Hossein Nejat (March 2017). "Effect of size on the chaotic behavior of nano resonators". Communications in Nonlinear Science and Numerical Simulation. 44: 495–505. Bibcode:2017CNSNS..44..495A. doi:10.1016/j.cnsns.2016.09.010.
• Crutchfield; Tucker; Morrison; J.D. Farmer; Packard; N.H.; Shaw; R.S (December 1986). "Chaos". Scientific American. 255 (6): 38–49 (bibliography p.136). Bibcode:1986SciAm.255d..38T. doi:10.1038/scientificamerican1286-46. Online version (Note: the volume and page citation cited for the online text differ from that cited here. The citation here is from a photocopy, which is consistent with other citations found online that don't provide article views. The online content is identical to the hardcopy text. Citation variations are related to country of publication).
• Kolyada, S.F. (2004). "Li-Yorke sensitivity and other concepts of chaos". Ukrainian Math. J. 56 (8): 1242–57. doi:10.1007/s11253-005-0055-4. S2CID 207251437.
• Day, R.H.; Pavlov, O.V. (2004). "Computing Economic Chaos". Computational Economics. 23 (4): 289–301. doi:10.1023/B:CSEM.0000026787.81469.1f. S2CID 119972392. SSRN 806124.
• Strelioff, C.; Hübler, A. (2006). "Medium-Term Prediction of Chaos" (PDF). Phys. Rev. Lett. 96 (4): 044101. Bibcode:2006PhRvL..96d4101S. doi:10.1103/PhysRevLett.96.044101. PMID 16486826. 044101. Archived from the original (PDF) on 2013-04-26.
• Hübler, A.; Foster, G.; Phelps, K. (2007). "Managing Chaos: Thinking out of the Box" (PDF). Complexity. 12 (3): 10–13. Bibcode:2007Cmplx..12c..10H. doi:10.1002/cplx.20159. Archived from the original (PDF) on 2012-10-30. Retrieved 2011-07-17.
• Motter, Adilson E.; Campbell, David K. (2013). "Chaos at 50". Physics Today. 66 (5): 27. arXiv:1306.5777. Bibcode:2013PhT....66e..27M. doi:10.1063/PT.3.1977. S2CID 54005470.

کتب درسی

• Alligood, K.T.; Sauer, T.; Yorke, J.A. (1997). Chaos: an introduction to dynamical systems. Springer-Verlag. ISBN 978-0-387-94677-1.
• Baker, G. L. (1996). Chaos, Scattering and Statistical Mechanics. Cambridge University Press. ISBN 978-0-521-39511-3.
• Badii, R.; Politi A. (1997). Complexity: hierarchical structures and scaling in physics. Cambridge University Press. ISBN 978-0-521-66385-4.
• Bunde; Havlin, Shlomo, eds. (1996). Fractals and Disordered Systems. Springer. ISBN 978-3-642-84870-4. and Bunde; Havlin, Shlomo, eds. (1994). Fractals in Science. Springer. ISBN 978-3-540-56220-7.
• Collet, Pierre, and Eckmann, Jean-Pierre (1980). Iterated Maps on the Interval as Dynamical Systems. Birkhauser. ISBN 978-0-8176-4926-5.{{cite book}}: نگهداری یادکرد:نام‌های متعدد:فهرست نویسندگان (link)
• Devaney, Robert L. (2003). An Introduction to Chaotic Dynamical Systems (2nd ed.). Westview Press. ISBN 978-0-8133-4085-2.^{[پیوند مرده]}
• Robinson, Clark (1995). Dynamical systems: Stability, symbolic dynamics, and chaos. CRC Press. ISBN 0-8493-8493-1.
• Feldman, D. P. (2012). Chaos and Fractals: An Elementary Introduction. Oxford University Press. ISBN 978-0-19-956644-0. Archived from the original on 31 December 2019. Retrieved 21 April 2021.
• Gollub, J. P.; Baker, G. L. (1996). Chaotic dynamics. Cambridge University Press. ISBN 978-0-521-47685-0.
• Guckenheimer, John; Holmes, Philip (1983). Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer-Verlag. ISBN 978-0-387-90819-9.
• Gulick, Denny (1992). Encounters with Chaos. McGraw-Hill. ISBN 978-0-07-025203-5.
• Gutzwiller, Martin (1990). Chaos in Classical and Quantum Mechanics. Springer-Verlag. ISBN 978-0-387-97173-5.
• Hoover, William Graham (2001) [1999]. Time Reversibility, Computer Simulation, and Chaos. World Scientific. ISBN 978-981-02-4073-8.
• Kautz, Richard (2011). Chaos: The Science of Predictable Random Motion. Oxford University Press. ISBN 978-0-19-959458-0.
• Kiel, L. Douglas; Elliott, Euel W. (1997). Chaos Theory in the Social Sciences. Perseus Publishing. ISBN 978-0-472-08472-2.
• Moon, Francis (1990). Chaotic and Fractal Dynamics. Springer-Verlag. ISBN 978-0-471-54571-2.
• Ott, Edward (2002). Chaos in Dynamical Systems. Cambridge University Press. ISBN 978-0-521-01084-9.
• Strogatz, Steven (2000). Nonlinear Dynamics and Chaos. Perseus Publishing. ISBN 978-0-7382-0453-6.
• Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 978-0-19-850840-3.
• Tél, Tamás; Gruiz, Márton (2006). Chaotic dynamics: An introduction based on classical mechanics. Cambridge University Press. ISBN 978-0-521-83912-9.
• Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.
• Thompson JM, Stewart HB (2001). Nonlinear Dynamics And Chaos. John Wiley and Sons Ltd. ISBN 978-0-471-87645-8.
• Tufillaro; Reilly (1992). An experimental approach to nonlinear dynamics and chaos. American Journal of Physics. Vol. 61. Addison-Wesley. p. 958. Bibcode:1993AmJPh..61..958T. doi:10.1119/1.17380. ISBN 978-0-201-55441-0.
• Wiggins, Stephen (2003). Introduction to Applied Dynamical Systems and Chaos. Springer. ISBN 978-0-387-00177-7.
• Zaslavsky, George M. (2005). Hamiltonian Chaos and Fractional Dynamics. Oxford University Press. ISBN 978-0-19-852604-9.

آثار نیمه-فنی و عرفی

• Christophe Letellier, Chaos in Nature, World Scientific Publishing Company, 2012, شابک ‎۹۷۸−۹۸۱−۴۳۷۴−۴۲−۲.
• Abraham, Ralph; et al. (2000). Abraham, Ralph H.; Ueda, Yoshisuke (eds.). The Chaos Avant-Garde: Memoirs of the Early Days of Chaos Theory. World Scientific Series on Nonlinear Science Series A. Vol. 39. World Scientific. Bibcode:2000cagm.book.....A. doi:10.1142/4510. ISBN 978-981-238-647-2.
• Barnsley, Michael F. (2000). Fractals Everywhere. Morgan Kaufmann. ISBN 978-0-12-079069-2.
• Bird, Richard J. (2003). Chaos and Life: Complexity and Order in Evolution and Thought. Columbia University Press. ISBN 978-0-231-12662-5.
• John Briggs and David Peat, Turbulent Mirror:: An Illustrated Guide to Chaos Theory and the Science of Wholeness, Harper Perennial 1990, 224 pp.
• John Briggs and David Peat, Seven Life Lessons of Chaos: Spiritual Wisdom from the Science of Change, Harper Perennial 2000, 224 pp.
• Cunningham, Lawrence A. (1994). "From Random Walks to Chaotic Crashes: The Linear Genealogy of the Efficient Capital Market Hypothesis". George Washington Law Review. 62: 546.
• Predrag Cvitanović, Universality in Chaos, Adam Hilger 1989, 648 pp.
• Leon Glass and Michael C. Mackey, From Clocks to Chaos: The Rhythms of Life, Princeton University Press 1988, 272 pp.
• James Gleick, Chaos: Making a New Science, New York: Penguin, 1988. 368 pp.
• John Gribbin (2005-01-27). Deep Simplicity. Penguin Press Science. Penguin Books.
• L Douglas Kiel, Euel W Elliott (ed.), Chaos Theory in the Social Sciences: Foundations and Applications, University of Michigan Press, 1997, 360 pp.
• Arvind Kumar, Chaos, Fractals and Self-Organisation; New Perspectives on Complexity in Nature , National Book Trust, 2003.
• Hans Lauwerier, Fractals, Princeton University Press, 1991.
• Edward Lorenz, The Essence of Chaos, University of Washington Press, 1996.
• Marshall, Alan (2002). The Unity of Nature - Wholeness and Disintegration in Ecology and Science. doi:10.1142/9781860949548. ISBN 978-1-86094-954-8.
• David Peak and Michael Frame, Chaos Under Control: The Art and Science of Complexity, Freeman, 1994.
• Heinz-Otto Peitgen and Dietmar Saupe (Eds.), The Science of Fractal Images, Springer 1988, 312 pp.
• Clifford A. Pickover, Computers, Pattern, Chaos, and Beauty: Graphics from an Unseen World , St Martins Pr 1991.
• Clifford A. Pickover, Chaos in Wonderland: Visual Adventures in a Fractal World, St Martins Pr 1994.
• Ilya Prigogine and Isabelle Stengers, Order Out of Chaos, Bantam 1984.
• Peitgen, Heinz-Otto; Richter, Peter H. (1986). The Beauty of Fractals. doi:10.1007/978-3-642-61717-1. ISBN 978-3-642-61719-5.
• David Ruelle, Chance and Chaos, Princeton University Press 1993.
• Ivars Peterson, Newton's Clock: Chaos in the Solar System, Freeman, 1993.
• Ian Roulstone; John Norbury (2013). Invisible in the Storm: the role of mathematics in understanding weather. Princeton University Press. ISBN 978-0-691-15272-1.
• Ruelle, D. (1989). Chaotic Evolution and Strange Attractors. doi:10.1017/CBO9780511608773. ISBN 978-0-521-36272-6.
• Manfred Schroeder, Fractals, Chaos, and Power Laws, Freeman, 1991.
• Smith, Peter (1998). Explaining Chaos. doi:10.1017/CBO9780511554544. ISBN 978-0-511-55454-4.
• Ian Stewart, Does God Play Dice?: The Mathematics of Chaos , Blackwell Publishers, 1990.
• Steven Strogatz, Sync: The emerging science of spontaneous order, Hyperion, 2003.
• Yoshisuke Ueda, The Road To Chaos, Aerial Pr, 1993.
• M. Mitchell Waldrop, Complexity: The Emerging Science at the Edge of Order and Chaos, Simon & Schuster, 1992.
• Antonio Sawaya, Financial Time Series Analysis: Chaos and Neurodynamics Approach, Lambert, 2012.

پیوند به بیرون

• "Chaos", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Nonlinear Dynamics Research Group with Animations in Flash
• The Chaos group at the University of Maryland
• The Chaos Hypertextbook. An introductory primer on chaos and fractals
• ChaosBook.org An advanced graduate textbook on chaos (no fractals)
• Society for Chaos Theory in Psychology & Life Sciences
• Nonlinear Dynamics Research Group at CSDC, Florence Italy
• Interactive live chaotic pendulum experiment, allows users to interact and sample data from a real working damped driven chaotic pendulum
• Nonlinear dynamics: how science comprehends chaos, talk presented by Sunny Auyang, 1998.
• Nonlinear Dynamics. Models of bifurcation and chaos by Elmer G. Wiens
• Gleick's Chaos (excerpt) بایگانی‌شده در ۲ فوریه ۲۰۰۷ توسط Wayback Machine
• Systems Analysis, Modelling and Prediction Group at the University of Oxford
• A page about the Mackey-Glass equation
• High Anxieties — The Mathematics of Chaos (2008) BBC documentary directed by David Malone
• The chaos theory of evolution – article published in Newscientist featuring similarities of evolution and non-linear systems including fractal nature of life and chaos.
• Jos Leys, Étienne Ghys et Aurélien Alvarez, Chaos, A Mathematical Adventure. Nine films about dynamical systems, the butterfly effect and chaos theory, intended for a wide audience.
• "Chaos Theory", BBC Radio 4 discussion with Susan Greenfield, David Papineau & Neil Johnson (In Our Time, ۱۶ مه ۲۰۰۲)