مقطع مخروطی

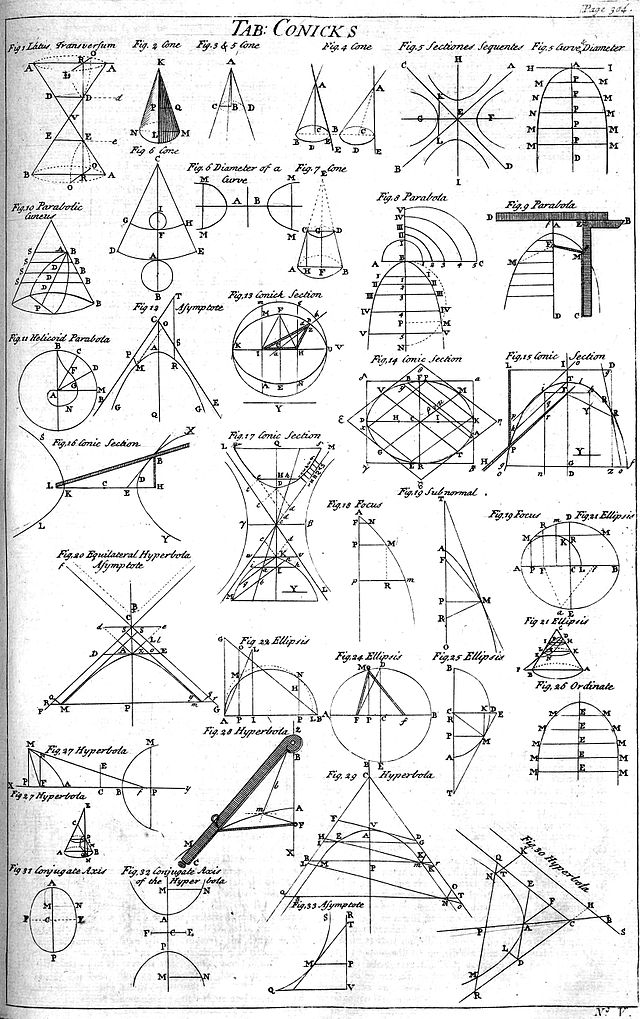
مقطع مخروطی (به انگلیسی: Conic section) به خمی گویند که از برخورد یک مخروط و یک صفحه حاصل شود.

انواع مقاطع مخروطی:
# دایره و بیضی
# هذلولی، سهمی

مخروطی، دانشنامه, ۱۷۲۸

اثبات اینکه در حالت غیر انحطاط این منحنی‌ها، که به عنوان منحنی‌های مکان در صفحه تعریف می‌شوند، واقعاً به وجود می‌آیند، می‌تواند بدون محاسبه با کمک کره‌های دندلین انجام شود. اثبات ریاضی در اینجا در مقاطع صفحه بخش مخروط واحد آورده شده‌است. یک مخروط همچنین می‌تواند به عنوان یک مورد خاص دو بعدی از یک چهارگانه دیده شود و می‌توان آن را با یک معادله درجه دوم، معادله مخروطی عمومی توصیف کرد. جاسازی یک بیضی، هذلولی و سهمی در یک صفحه نمایشی منجر به مخروط‌های تصویری می‌شود که همگی معادل یکدیگر هستند، یعنی؛ یعنی می‌توان آنها را با نگاشت خط مستقیم به یکدیگر تبدیل کرد.

معادلهٔ کلی

معادلهٔ یک مقطع مخروطی به‌صورت معادلهٔ درجه دو زیر برحسب ${\displaystyle x,y}$ بیان می‌شود:^[۱]

${\displaystyle ax^{2}+2hxy+by^{2}+2gx+2fy+c=0}$

صفحات مقاطع مخروطی

برای تعیین اینکه منحنی ها/نقاطی که در بالا به عنوان مقاطع مخروطی به آنها اشاره شد در واقع زمانی رخ می‌دهند که یک مخروط یک صفحه را قطع می‌کند، در اینجا مخروط واحد را قطع می‌کنیم (مستقیم مخروط دایره ای) ${\displaystyle K_{1}\colon x^{2}+y^{2}=z^{2}}$ با صفحه موازی با محور y. این یک محدودیت نیست زیرا مخروط به صورت چرخشی متقارن است. هر مخروط دایره‌ای سمت راست، تصویر پیوندی مخروط واحد ${\displaystyle K_{1}}$ است و بیضی‌ها/hyperbolas/parabolas/... با یک نقشه‌برداری affine به همان شکل برگردید. داده شده: صفحه ${\displaystyle \varepsilon \colon ax+cz=d\ ,}$ مخروط ${\displaystyle K_{1}\colon x^{2}+y^{2}=z^{2}}$. جستجو: تقاطع ${\displaystyle \varepsilon \cap K_{1}}$.

• Fall I: ${\displaystyle c=0}$ In diesem Fall ist die Ebene senkrecht und ${\displaystyle a\neq 0}$ und ${\displaystyle x=d/a}$. Eliminiert man ${\displaystyle x}$ aus der Kegelgleichung, so erhält man ${\displaystyle z^{2}-y^{2}=d^{2}/a^{2}}$.
  • Fall Ia: ${\displaystyle d=0}$. In diesem Fall besteht der Schnitt aus dem Geradenpaar ${\displaystyle t(0,1,\pm 1),\ t\in \mathbb {R} .}$.
  • Fall Ib: ${\displaystyle d\neq 0}$. Die obige Gleichung beschreibt jetzt eine Hyperbel in der y-z-Ebene. Also ist auch die Schnittkurve ${\displaystyle \varepsilon \cap K_{1}}$ selbst eine Hyperbel.
• Fall II: ${\displaystyle c\neq 0}$. Eliminiert man ${\displaystyle z}$ aus der Kegelgleichung mit Hilfe der Ebenengleichung, so erhält man das Gleichungssystem ${\displaystyle (1)\quad (c^{2}-a^{2})x^{2}+2adx+c^{2}y^{2}=d^{2},\qquad (2)\quad ax+cz=d.}$
  • Fall IIa: Für ${\displaystyle d=0}$ geht die Ebene durch die Kegelspitze ${\displaystyle (0,0,0)}$ und Gleichung (1) hat jetzt die Gestalt ${\displaystyle (c^{2}-a^{2})x^{2}+c^{2}y^{2}=0}$.

    Für ${\displaystyle c^{2}>a^{2}}$ ist der Schnitt der Punkt ${\displaystyle P_{0}=(0,0,0)}$.

    Für ${\displaystyle c^{2}=a^{2}}$ ist der Schnitt die Gerade ${\displaystyle t(c,0,-a),\ t\in \mathbb {R} .}$

    Für ${\displaystyle c^{2}<a^{2}}$ ist der Schnitt das Geradenpaar ${\displaystyle t(c/\pm {\sqrt {a^{2}-c^{2}}},1,-a/\pm {\sqrt {a^{2}-c^{2}}}),\ t\in \mathbb {R} .}$

  • Fall IIb: Für ${\displaystyle d\neq 0}$ geht die Ebene nicht durch die Kegelspitze und ist nicht senkrecht.

    Für ${\displaystyle c^{2}=a^{2}}$ geht (1) in ${\displaystyle x=-{\frac {c^{2}}{2ad}}y^{2}+{\frac {d}{2a}}}$ über und die Schnittkurve ist eine Parabel.

    Für ${\displaystyle c^{2}\neq a^{2}}$ formen wir (1) um in ${\displaystyle {\frac {(c^{2}-a^{2})^{2}}{d^{2}c^{2}}}\left(x+{\frac {ad}{c^{2}-a^{2}}}\right)^{2}+{\frac {c^{2}-a^{2}}{d^{2}}}y^{2}=1}$.

    Für ${\displaystyle c^{2}>a^{2}}$ ergibt sich als Schnittkurve eine Ellipse und

    für ${\displaystyle c^{2}<a^{2}}$ ergibt sich eine Hyperbel.

Parameterdarstellungen der Schnittkurven findet man in Weblink CDKG, S. 106–107.

Zusammenfassung:

• Enthält die Schnittebene die Kegelspitze nicht, entstehen die nicht ausgearteten Kegelschnitte (s. Bild zu Ib, IIb), nämlich eine Parabel, eine Ellipse oder eine Hyperbel, je nachdem, ob die Kegelachse von der Schnittebene unter dem gleichen, einem größeren oder einem kleineren Winkel geschnitten wird als von den Mantellinien des Kegels.
• Liegt hingegen die Kegelspitze in der Schnittebene, entstehen die ausgearteten Kegelschnitte (s. Bild zu Ia, IIa), und zwar ein Punkt (nämlich die Kegelspitze), eine Gerade (nämlich eine Mantellinie) oder ein sich schneidendes Geradenpaar, (nämlich zwei Mantellinien).

• 
  Parabel
  Entsteht, wenn der Neigungswinkel ${\displaystyle \beta }$ der Schnittebene gleich dem Neigungswinkel ${\displaystyle \alpha }$ der Mantellinie des Kegels ist.
• 
  Ellipse
  Entsteht, wenn der Neigungswinkel ${\displaystyle \beta }$ der Schnittebene kleiner ist als der Neigungswinkel ${\displaystyle \alpha }$ der Mantellinie des Kegels.
• 
  Hyperbel
  Entsteht, wenn der Neigungswinkel ${\displaystyle \beta }$ der Schnittebene größer ist als der Neigungswinkel ${\displaystyle \alpha }$ der Mantellinie des Kegels.
• 
  Kreis
  Entsteht, wenn die Achse des Kegels eine Orthogonale zur Schnittebene ist.
• 
  Punkt
  Entsteht, wenn die Schnittebene durch die Kegelpitze verläuft.
  Gerade
  Entsteht, wenn die Schnittebene entlang der Mantellinie durch die Kegelspitze verläuft.
• 
  Geradenpaar
  Entsteht, wenn die Schnittebene durch die Kegelspitze und Mantelfläche verläuft.

معادله قطبی در مقاطع مخروطی

Die Leitlinieneigenschaft der nicht ausgearteten Kegelschnitte lautet:

• Die Menge der Punkte der euklidischen Ebene, deren Abstände zu einer vorgegebenen Geraden ${\displaystyle l}$ und einem vorgegebenen Punkt ${\displaystyle F}$ die Bedingung ${\displaystyle {\frac {|PF|}{|Pl|}}=\varepsilon >0}$ ist konstant, erfüllen, ist eine Ellipse, falls ${\displaystyle 0<\varepsilon <1}$, eine Parabel, falls ${\displaystyle \varepsilon =1}$, eine Hyperbel, falls ${\displaystyle \varepsilon >1}$ ist.

Ist der Punkt ${\displaystyle F}$ der Nullpunkt und hat die Gerade ${\displaystyle l}$ die Gleichung ${\displaystyle x=-d}$, so gilt in Polarkoordinaten (s. Bild):

${\displaystyle {\frac {|PF|}{|Pl|}}={\frac {r}{r\cos \varphi +d}}=\varepsilon \ .}$

Auflösen nach ${\displaystyle r}$ liefert zunächst ${\displaystyle r={\frac {\varepsilon d}{1-\varepsilon \cos \varphi }}}$. Setzt man ${\displaystyle p=r(\pi /2)=\varepsilon d}$, so erhält man die Polardarstellung der nichtausgearteten Kegelschnitte:

• ${\displaystyle r={\frac {p}{1-\varepsilon \cos \varphi }}}$.

${\displaystyle p}$ ist dabei der Halbparameter (halbe Breite des Kegelschnitts am Brennpunkt) und ${\displaystyle \varepsilon }$ die numerische Exzentrizität. Wählt man den Halbparameter ${\displaystyle p}$ fest, so erhält man Kegelschnitte mit dem Nullpunkt als gemeinsamen Brennpunkt, und zwar

für ${\displaystyle \varepsilon =0}$ den Kreis mit Mittelpunkt ${\displaystyle M=(0,0)}$ und Radius ${\displaystyle R=p}$,

für ${\displaystyle 0<\varepsilon <1}$ die Ellipse mit dem Mittelpunkt ${\displaystyle M=(e,0),\ e={\frac {p\;\varepsilon }{1-\varepsilon ^{2}}}}$ und den Halbachsen ${\displaystyle a={\frac {e}{\varepsilon }},\ b={\sqrt {a^{2}-e^{2}}}}$,

für ${\displaystyle \varepsilon =1}$ die Parabel mit dem Scheitel ${\displaystyle S=(-{\frac {p}{2}},0)}$ und der Gleichung ${\displaystyle x={\frac {y^{2}-p^{2}}{2p}}}$,

für ${\displaystyle \varepsilon >1}$ die Hyperbel mit dem Mittelpunkt ${\displaystyle M=(-e,0),\ e={\frac {p\;\varepsilon }{\varepsilon ^{2}-1}}}$ und den Halbachsen ${\displaystyle a={\frac {e}{\varepsilon }},\ b={\sqrt {e^{2}-a^{2}}}}$.

دوران شکل‌ها

از دوران هر شکل دور یک محورش شکل جدیدی به وجود می‌آید.

مثلاً از دوران مستطیل حول یک محورش، استوانه به دست می‌آید.

مثلاً پاره‌خطی را حول خطی که بر آن عمود است دوران دهیم، یک دایره ایجاد می‌شود.

برش

مخروطی را در نظر بگیرید. اگر برشی موازی قاعدهٔ آن روی آن ایجاد کنیم، سطح مقطع به وجود آمده یک دایره است. اگر این برش را به صورت مایل به طوری‌که نه موازی قاعده و نه موازی مولد مخروط باشد، سطح مقطع ایجاد شده یک بیضی خواهد بود. اگر این برش موازی مولد مخروط باشد، سطح مقطع به وجود آمده سهمی نامیده می‌شود. و اگر این برش بر قاعده عمود شود یک هذلولی ایجاد می‌شود.

دایره[۲]

دایره یک منحنی مسطح و بسته و شامل نقاطی از صفحه است که فاصله‌شان از نقطهٔ ثابتی واقع در آن صفحه مقداری ثابت باشد. نقطهٔ ثابت، مرکز دایره و مقدار ثابت، اندازهٔ شعاع دایره نامیده می‌شود. همچنین دایره را می‌توان یک بیضی دانست که کانون‌های آن بر همدیگر منطبقند (برون‌مرکزی آن صفر است)؛ ازین‌رو دایره یکی از مقاطع مخروطی است. مقطع مخروطی منحنی‌ای است که در محل تقاطع یک صفحه با یک مخروط پدیدار می‌شود، و هنگامی که صفحه با مقطع مخروط موازی باشد منحنی حاصل دایره خواهد بود. دایره را همچنین می‌توان به عنوان چندضلعی متساوی‌الاضلاعی تعریف کرد که تعداد اضلاع آن به بی‌نهایت میل می‌کند.

بیضی

بیضی مجموعهٔ نقاطی از صفحه است که جمع فواصل آن نقاط از دو نقطهٔ ثابت در صفحه، عددی ثابت است.

به این دو نقطه ثابت کانون‌های بیضی گفته می‌شود و فاصله این دو را فاصلهٔ کانونی می‌نامند. بیضی دارای دو قطر می‌باشد که برهم عمود هستند و به محل برخورد این دو قطر مرکز بیضی گفته می‌شود.

سهمی[۳]

سهمی مجموعه نقاطی از صفحه است که از یک خط و از یک نقطه هم فاصله هستند. سهمی خمی باز است که از برخورد مخروطی قائم با قاعدهٔ دایره‌ای و صفحه‌ای حاصل می‌شود که با یکی از وترهای مخروط موازی باشد ولی با ارتفاع مخروط موازی نباشد. اگر این صفحه با قاعدهٔ مخروط موازی باشد حاصل دایره، اگر با ارتفاع مخروط موازی باشد حاصل هذلولی، و اگر با هیچ‌یک از وترهای مخروط یا ارتفاع آن موازی نباشد حاصل بیضی خواهد بود.

هذلولی[۴]

هُذلولی خمی باز است که از برخورد یک صفحه با سطح مخروطی، در حالتی که صفحه، موازی با محورِ سطحِ مخروطی باشد، پدید می‌آید. در صفحهٔ اقلیدسی و از نظر مکان هندسی، هذلولی مجموعه‌ای از نقاط در یک صفحه است که تفاضل فاصلهٔ هر یک از آن‌ها از دو نقطهٔ ثابت در صفحه (کانون‌ها)، مقداری ثابت (دو برابر مقدار a در هذلولی) باشد؛ اگر نصف اندازهٔ طول و عرض هذلولی را a و b و نصف فاصلهٔ کانونی را c بنامیم، در هر هذلولی رابطهٔ c² = a² + b² برقرار خواهد بود. هر هذلولی دو خط مجانب دارد که در مرکز هذلولی با هم برخورد می‌کنند.

پانویس

مقاطع مخروطی

جستارهای وابسته

• دستگاه مختصات دائرةالبروجی

منابع

1. Sharma, p. 150
2. تحقیق از طریق مقاله:دایره
3. تحقیق از طریق سهمی
4. تحقیق از طریق:هذلولی

• Sharma, A.K. (2005). Text Book of Conic Section. Discovery Publishing House. ISBN 8183560008, 9788183560009. {{cite book}}: Check |isbn= value: invalid character (help); Cite has empty unknown parameter: |coauthors= (help)

پیوند به بیرون

• Conic section (Geometry) در دانشنامهٔ بریتانیکا