Sistema cristalino

Un sólido cristalino se construye a partir de la repetición en el espacio de una estructura elemental paralelepipédica denominada celda unitaria. Los siete sistemas de cristal son triclínico, monoclínico, ortorrómbico, tetragonal,trigonal, hexagonal y cúbico. Informalmente, dos cristales están en el mismo sistema cristalino si tienen simetrías similares (aunque hay muchas excepciones).

Celda unitaria

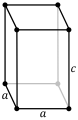
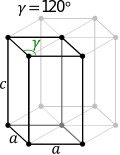
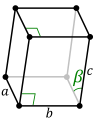
En función de los parámetros de red, es decir, de las longitudes de los lados o ejes del paralelepípedo elemental y de los ángulos que forman, se distinguen siete sistemas cristalinos:

Sistema cristalino	Ejes	Ángulos entre ejes
Cúbico	a = b = c	α = β = γ = 90°
Tetragonal	a = b ≠ c	α = β = γ = 90°
Ortorrómbico (o Rómbico)	a ≠ b ≠ c	α = β = γ = 90°
Hexagonal	a = b ≠ c	α = β = 90°; γ = 120°
Trigonal (o Romboédrico)	a = b = c	α = β = γ ≠ 90°
Monoclínico	a ≠ b ≠ c	α = γ = 90°; β ≠ 90°
Triclínico	a ≠ b ≠ c	α ≠ β ≠ γ α, β, γ ≠ 90°

En función de las posibles localizaciones de los átomos en la celda unitaria se establecen 14 estructuras cristalinas básicas, las denominadas redes de Bravais.

Clasificaciones

Los cristales se pueden clasificar de tres maneras: sistemas de cristales, familias de cristales y sistemas de entramado. Éstos utilizan grupo espacial, redes y grupo puntual. Las distintas clasificaciones se confunden a menudo: en particular, el sistema cristalino trigonal se confunde a menudo con el sistema de red romboédrica, y el término "sistema cristalino" se utiliza a veces para referirse a uno de los otros.

Los espacios con menos de tres dimensiones tienen el mismo número de sistemas de cristales, familias de cristales y sistemas de red. En un espacio unidimensional, hay un sistema de cristales. En el espacio 2D, hay cuatro sistemas de cristales: oblicuo, rectangular, cuadrado y hexagonal.

Familia de cristales

Una familia de cristales está determinada por las redes y los grupos de puntos. Se forma combinando sistemas cristalinos que tienen grupos espaciales asignados a un sistema de red común. En tres dimensiones, las familias y los sistemas de cristales son idénticos, excepto los sistemas de cristales hexagonales y trigonales, que se combinan en una familia de cristales hexagonales. Las seis familias de cristales son triclínica, monoclínica, ortorrómbica, tetragonal, hexagonal y cúbica.

Cristal hexagonal de hanksita, con simetría en el eje c

Sistema de red cristalina

Un sistema de red cristalina es un grupo de redes cristalinas con el mismo conjunto de grupos de puntos, que son subgrupos del clases aritméticas de cristales. Los grupos espaciales y los cristales se clasifican como sistemas reticulares según sus redes de Bravais. Los 14 entramados de Bravais se agrupan en siete sistemas de entramado: triclínico, monoclínico, ortorrómbico, tetragonal, romboédrico, hexagonal y cúbico.

Cinco de los sistemas cristalinos son esencialmente iguales a cinco de los sistemas de red, mientras que los sistemas cristalinos hexagonales y trigonales son diferentes.

La mayoría de los grupos de puntos se asignan a un único sistema de red, en cuyo caso tanto el cristal como el sistema de red tienen el mismo nombre. Sin embargo, cinco grupos de puntos se asignan a dos sistemas de red, el romboédrico y el hexagonal, porque ambos presentan una triple simetría rotacional. Estos grupos de puntos se asignan al sistema cristalino trigonal.

La relación entre las familias de cristales tridimensionales, los sistemas de cristales y los sistemas de red se muestra en la siguiente tabla:

Familia de cristales	Sistema de cristales	Simetrías requeridas del grupo de puntos	Grupos de puntos	Grupo espacial	Redes de Bravais	Sistema de red
Triclínico	Triclínico	Ninguno	2	2	1	Triclínico
Monoclínico	Monoclínico	1 doble eje de rotación o 1 plano de espejo	3	13	2	Monoclínico
Ortorrómbico	Ortorrómbico	3 ejes de rotación dobles o 1 eje de rotación doble y 2 planos de espejo	3	59	4	Ortorrómbico
Sistema cristalino tetragonal	Tetragonal	1 eje de rotación cuádruple	7	68	2	Tetragonal
Hexagonal	Trigonal	1 eje de rotación triple	5	7	1	Romboedro
				18	1	Hexagonal
	Hexagonal	1 eje de rotación séxtuple	7	27
Cúbico	Cúbico	4 ejes triples de rotación	5	36	3	Cúbico
6	7	Total	32	230	14	7

Nota: no existe un sistema de entramado "trigonal". Para evitar la confusión de la terminología, el término "celosía trigonal" no se utiliza.

Elementos de simetría

El tipo de sistema normal cristalino depende de la disposición simétrica y repetitiva de las caras que forman el cristal. Dicha disposición es consecuencia del ordenamiento interno de sus átomos y, por lo tanto, característico de cada mineral. Las caras se dispondrán según los elementos de simetría que tenga ese sistema, siendo uno de ellos característico de cada uno de los siete sistemas:

Sistema cristalino	Elementos característicos
Cúbico	Cuatro ejes ternarios
Tetragonal	Un eje cuaternario (o binario derivado)
Ortorrómbico	Tres ejes binarios o tres planos de simetría
Hexagonal	Un eje senario (o ternario derivado)
Trigonal (o Romboédrica)	Un eje ternario
Monoclínico	Un eje binario o un plano de simetría
Triclínico	Un centro de simetría o bien ninguna simetría

Tipos

• 
  Cúbico
• 
  Tetragonal
• 
  Ortorrómbico
• 
  Hexagonal
• 
  Romboédrico
• 
  Monoclínico
• 
  Triclínico

En otras dimensiones

Espacio bidimensional

El espacio bidimensional tiene el mismo número de sistemas de cristal, familias de cristal y sistemas de celosía. En el espacio 2D, hay cuatro sistemas de cristal: oblicuo, rectangular, cuadrado y hexagonal.

Espacio de cuatro dimensiones

‌La celda unitaria de cuatro dimensiones se define por cuatro longitudes de borde (a, b, c, d) ay seis ángulos interaxiales (α, β, γ, δ, ε, ζ). Las siguientes condiciones para los parámetros de la red definen 23 familias de cristales

Familias de cristal en espacio de 4 dimensiones (4D)

N.º	Familia	Longitudes de borde	Ángulos interaxiales
1	Hexaclínico	a ≠ b ≠ c ≠ d	α ≠ β ≠ γ ≠ δ ≠ ε ≠ ζ ≠ 90°
2	Triclínico	a ≠ b ≠ c ≠ d	α ≠ β ≠ γ ≠ 90° δ = ε = ζ = 90°
3	Diclínico	a ≠ b ≠ c ≠ d	α ≠ 90° β = γ = δ = ε = 90° ζ ≠ 90°
4	Monoclínico	a ≠ b ≠ c ≠ d	α ≠ 90° β = γ = δ = ε = ζ = 90°
5	Ortogonal	a ≠ b ≠ c ≠ d	α = β = γ = δ = ε = ζ = 90°
6	Monoclínico tetragonal	a ≠ b = c ≠ d	α ≠ 90° β = γ = δ = ε = ζ = 90°
7	Monoclínico hexagonal	a ≠ b = c ≠ d	α ≠ 90° β = γ = δ = ε = 90° ζ = 120°
8	Diclínico ditetragonal	a = d ≠ b = c	α = ζ = 90° β = ε ≠ 90° γ ≠ 90° δ = 180° − γ
9	Diclínico ditrigonal (dihexagonal)	a = d ≠ b = c	α = ζ = 120° β = ε ≠ 90° γ ≠ δ ≠ 90° cos δ = cos β − cos γ
10	Ortogonal tetragonal	a ≠ b = c ≠ d	α = β = γ = δ = ε = ζ = 90°
11	Ortogonal hexagonal	a ≠ b = c ≠ d	α = β = γ = δ = ε = 90°, ζ = 120°
12	Monoclínico ditetragonal	a = d ≠ b = c	α = γ = δ = ζ = 90° β = ε ≠ 90°
13	Ditrigonal (dihexagonal) monoclínico	a = d ≠ b = c	α = ζ = 120° β = ε ≠ 90° γ = δ ≠ 90° cos γ = −1/2cos β
14	Ditetragonal ortogonal	a = d ≠ b = c	α = β = γ = δ = ε = ζ = 90°
15	Tetragonal hexagonal	a = d ≠ b = c	α = β = γ = δ = ε = 90° ζ = 120°
16	Dihexagonal ortogonal	a = d ≠ b = c	α = ζ = 120° β = γ = δ = ε = 90°
17	Cúbico ortogonal	a = b = c ≠ d	α = β = γ = δ = ε = ζ = 90°
18	Octagonal	a = b = c = d	α = γ = ζ ≠ 90° β = ε = 90° δ = 180° − α
19	Decagonal	a = b = c = d	α = γ = ζ ≠ β = δ = ε cos β = −1/2 − cos α
20	Dodecagonal	a = b = c = d	α = ζ = 90° β = ε = 120° γ = δ ≠ 90°
21	Diisohexagonal ortogonal	a = b = c = d	α = ζ = 120° β = γ = δ = ε = 90°
22	Icosagonal (icosaedro)	a = b = c = d	α = β = γ = δ = ε = ζ cos α = −1/4
23	Hipercúbico	a = b = c = d	α = β = γ = δ = ε = ζ = 90°

Los nombres aquí se dan según Whittaker.^[1] Son casi los mismos que en Brown et al,^[2] con excepción de los nombres de las familias de cristales 9, 13 y 22. Los nombres de estas tres familias según Brown et al se dan entre paréntesis.

La relación entre las familias de cristales cuatridimensionales, los sistemas cristalinos y los sistemas reticulares se muestra en la siguiente tabla.^[1][2] Los sistemas enantiomórficos están marcados con un asterisco. El número de pares enantiomórficos se da entre paréntesis. Aquí, el término "enantiomórfico" tiene un significado diferente al de la tabla para las clases de cristales tridimensionales. Esto último significa que los grupos puntuales enantiomórficos describen estructuras quirales (enantiomórficas). En la tabla actual, "enantiomórfico" significa que un grupo en sí mismo (considerado como un objeto geométrico) es enantiomórfico, como pares enantiomórficos de grupos espaciales tridimensionales P3₁ y P3₂, P4₁22 y P4₃22. A partir del espacio de cuatro dimensiones, los grupos puntuales también pueden ser enantiomórficos en este sentido.

Sistemas de cristal en el espacio 4D

N.º de familia cristalina	Familia de cristal	Sistema de cristal	N.º de sistema de cristal de	Grupos de puntos	Grupos espaciales	Redes de Bravais	Sistema de celosía
I	Hexaclínico		1	2	2	1	P hexaclínico
II	Triclínico		2	3	13	2	P, S triclínico
III	Diclínico		3	2	12	3	P, S, D diclínico
IV	Monoclínico		4	4	207	6	P, S, S, I, D, F monoclínico
V	Ortogonal	Ortogonal no axial	5	2	2	1	Ortogonal KU
					112	8	Ortogonal P, S, I, Z, D, F, G, U
		Ortogonal axial	6	3	887
VI	Monoclínico tetragonal		7	7	88	2	Tetragonal monoclínico P, I
VII	Hexagonal monoclínico	Trigonal monoclínico	8	5	9	1	Hexagonal monoclínico R
					15	1	Hexagonal monoclínico P
		Hexagonal monoclínico	9	7	25
VIII	Diclínico ditetragonal*		10	1 (+1)	1 (+1)	1 (+1)	Diclínico ditetragonal P*
IX	Diclínico ditetragonal*		11	2 (+2)	2 (+2)	1 (+1)	Diclínico ditrigonal P*
X	Ortogonal tetragonal	Ortogonal tetragonal inversa	12	5	7	1	Ortogonal tetragonal KG
					351	5	Ortogonal tetragonal P, S, I, Z, G
		Ortogonal tetragonal propia	13	10	1312
XI	Ortogonal hexagonal	Ortogonal trigonal	14	10	81	2	Ortogonal hexagonal R, RS
					150	2	Ortogonal hexagonal P, S
		Ortogonal hexagonal	15	12	240
XII	Monoclínico ditetragonal*		16	1 (+1)	6 (+6)	3 (+3)	Monoclínico ditetragonal P*, S*, D*
XIII	Monoclínico ditrigonal*		17	2 (+2)	5 (+5)	2 (+2)	Monoclínico ditrigonal P*, RR*
XIV	Ditetragonal ortogonal	Cripto-ditetragonal ortogonal	18	5	10	1	Ditetragonal ortogonal D
					165 (+2)	2	Ditetragonal ortogonal P, Z
		Ditetragonal ortogonal	19	6	127
XV	Hexagonal tetragonal		20	22	108	1	Hexagonal tetragonal P
XVI	Dihexagonal ortogonal	Cripto-ditrigonal ortogonal*	21	4 (+4)	5 (+5)	1 (+1)	Dihexagonal ortogonal G*
					5 (+5)	1	Dihexagonal ortogonal P
		Dihexagonal ortogonal	23	11	20
		ditrigonal ortogonal	22	11	41
					16	1	Dihexagonal ortogonal RR
XVII	Ortogonal cúbico	Ortogonal cúbico simple	24	5	9	1	Ortogonal cúbico KU
					96	5	Ortogonal cúbico P, I, Z, F, U
		Ortogonal cúbico complejo	25	11	366
XVIII	Octagonal*		26	2 (+2)	3 (+3)	1 (+1)	Octagonal P*
XIX	Decagonal		27	4	5	1	Decagonal P
XX	Dodecagonal*		28	2 (+2)	2 (+2)	1 (+1)	Dodecagonal P*
XXI	Ortogonal diisohexagonal	Ortogonal diisohexagonal simple	29	9 (+2)	19 (+5)	1	Ortogonal diisohexagonal RR
					19 (+3)	1	Ortogonal diisohexagonal P
		Ortogonal diisohexagonal complejo	30	13 (+8)	15 (+9)
XXII	Icosagonal		31	7	20	2	Icosagonal P, SN
XXIII	Hipercúbico	Hipercúbico octagonalc	32	21 (+8)	73 (+15)	1	Hipercúbico P
					107 (+28)	1	Hipercúbico Z
		Hipercúbico dodecagonal	33	16 (+12)	25 (+20)
Total	23 (+6)	33 (+7)		227 (+44)	4783 (+111)	64 (+10)	33 (+7)

Véase también

• Estructura cristalina
• Grupo espacial
• Notación de Hermann-Mauguin