Bivector

En matemáticas, un bivector o 2-vector es una cantidad en álgebra exterior o álgebra geométrica que amplía la idea de escalares y vectores. Si un escalar se considera una cantidad de orden cero, y un vector es una cantidad de orden uno, entonces se puede considerar que un bivector es de orden dos.

Sectores de planos paralelos y con la misma orientación y área, se corresponden con el mismo bivector a ∧ b.^[1]

Los bivectores tienen aplicaciones en muchas áreas de las matemáticas y la física. Están relacionados con los números complejos en dos dimensiones y con los vectores axiales y los cuaterniones en tres dimensiones. Se pueden usar para generar rotaciones en cualquier número de dimensiones, y son una herramienta útil para clasificar tales rotaciones. También se utilizan en física, uniendo varias cantidades no relacionables de otra manera.

El producto exterior aplicado sobre los vectores genera bivectores: dados dos vectores a y b, su producto exterior a ∧ b es un bivector, al igual que la suma de cualquier bivector. No todos los bivectores se pueden generar como un solo producto exterior. Más precisamente, un bivector que se puede expresar como un producto exterior se llama simple. En hasta tres dimensiones, todos los bivectores son simples, pero en dimensiones superiores no es así.^[2] El producto exterior de dos vectores es anticonmutativo y alternante, por lo que b ∧ a es el opuesto del bivector a ∧ b, que produce la orientación opuesta, y a ∧ a es el bivector cero.

Geométricamente, un bivector simple se puede interpretar como un sector plano orientado, de forma análoga a pensar en un vector como un segmento con una dirección dada.^[3] El bivector a ∧ b tiene una magnitud igual al área del paralelogramo con lados a y b; tiene la colocación del plano que abarca a y b; y tiene el sentido de la rotación que alinearía a con b.^[3][4]

En términos simples, cualquier superficie se asimila al mismo bivector si tiene la misma área, la misma orientación y es paralela al mismo plano (véase la figura).

Historia

El bivector fue definido por primera vez en 1844 por el matemático alemán Hermann Grassmann en álgebra exterior como el resultado del producto exterior de dos vectores. Apenas el año anterior, en Irlanda, Hamilton había descubierto el cuaternión. Habría que esperar hasta 1888 para que el matemático inglés William Kingdon Clifford agregase el producto geométrico al álgebra de Grassmann, incorporando las ideas de Hamilton y de Grassmann. De la fusión de las dos ideas surgió la denominada álgebra de Clifford, gracias a la que el bivector se entendió completamente tal como se conoce hoy en día.

Alrededor de esta época, Josiah Willard Gibbs y Oliver Heaviside desarrollaron el cálculo vectorial, que incluía el producto vectorial y el producto escalar separados, deducidos a partir de la multiplicación de cuaterniones.^[5][6][7] El éxito del cálculo vectorial y del libro Análisis Vectorial de Gibbs y Wilson tuvo el efecto de que las ideas de Hamilton y Clifford se pasaran por alto durante mucho tiempo, ya que gran parte de las matemáticas y física del siglo XX se formularon utilizando vectores. Gibbs utilizó los vectores para desempeñar el papel de los bivectores en tres dimensiones, y se sirvió de los bivectores para describir cantidades no relacionadas, un uso que a veces se ha copiado.^[8][9][10] Hoy en día, los bivectores se estudian ampliamente como parte del álgebra geométrica, un álgebra de Clifford sobre un espacio vectorialreal o complejo dotado de una forma cuadrática no degenerada. Su resurgimiento fue liderado por David Hestenes, que junto con otros investigadores, aplicó el álgebra geométrica a una gama de nuevas aplicaciones en física.^[11]

Conceptos generales

Para este artículo, el bivector se considerará solo en álgebras geométricas reales. Esto en la práctica no es una restricción, ya que todas las aplicaciones útiles se extraen de tales álgebras. Además, a menos que se indique lo contrario, todos los ejemplos poseen una métrica euclídea y, por lo tanto, una forma cuadrática definida-positiva asociada.

El álgebra geométrica y el producto geométrico

El bivector surge de la definición del producto geométrico sobre un espacio vectorial. Para los vectores a, b y c, el producto geométrico de los vectores se define de la siguiente manera:

Asociatividad (álgebra)

${\displaystyle (\mathbf {ab} )\mathbf {c} =\mathbf {a} (\mathbf {bc} )}$

Distributividad a izquierda y a derecha

${\displaystyle {\begin{aligned}\mathbf {a} (\mathbf {b} +\mathbf {c} )&=\mathbf {ab} +\mathbf {ac} \\(\mathbf {b} +\mathbf {c} )\mathbf {a} &=\mathbf {ba} +\mathbf {ca} \end{aligned}}}$

Contracción

${\displaystyle {\mathbf {a} }^{2}=Q(\mathbf {a} )=\epsilon _{\mathbf {a} }{\left|\mathbf {a} \right|}^{2}}$
donde Q es la forma cuadrática, |a| es la magnitud de a y ϵ_a es la signatura del vector. Para un espacio con métrica euclidiana ϵ_a es 1, se puede omitir, y la condición de contracción es:

${\displaystyle {\mathbf {a} }^{2}={\left|\mathbf {a} \right|}^{2}}$

El producto interior

De la asociatividad a(ab) = a²b, un escalar que multiplica a b. Cuando b no es paralelo a y, por lo tanto, no es un múltiplo escalar de a, ab no puede ser un escalar. Pero

${\displaystyle {\frac {1}{2}}(\mathbf {ab} +\mathbf {ba} )={\frac {1}{2}}((\mathbf {a} +\mathbf {b} )^{2}-\mathbf {a} ^{2}-\mathbf {b} ^{2})}$

es una suma de escalares y por lo tanto es un escalar. A partir del teorema del coseno en el triángulo formado por los vectores, su valor es |a||b| cosθ, donde θ es el ángulo entre los vectores. Por lo tanto, es idéntico al producto interior entre dos vectores, y se escribe de la misma manera:

${\displaystyle \mathbf {a} \cdot \mathbf {b} ={\frac {1}{2}}(\mathbf {ab} +\mathbf {ba} ).}$

Es simétrico, tiene valor escalar y se puede utilizar para determinar el ángulo entre dos vectores: en particular, si a y b son ortogonales, el producto es cero.

El producto exterior

Al igual que el producto interior se puede formular como la parte simétrica del producto geométrico de otra cantidad, el producto exterior se puede formular como su parte antisimétrica:

${\displaystyle \mathbf {a} \wedge \mathbf {b} ={\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )}$

Es antisimétrico en a y b

${\displaystyle \mathbf {b} \wedge \mathbf {a} ={\frac {1}{2}}(\mathbf {ba} -\mathbf {ab} )=-{\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )=-\mathbf {a} \wedge \mathbf {b} }$

y por adición:

${\displaystyle \mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} ={\frac {1}{2}}(\mathbf {ab} +\mathbf {ba} )+{\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )=\mathbf {ab} }$

Es decir, el producto geométrico es la suma del producto interior simétrico y del producto exterior antisimétrico.

Para examinar la naturaleza de a ∧ b, considérese la fórmula

${\displaystyle (\mathbf {a} \cdot \mathbf {b} )^{2}-(\mathbf {a} \wedge \mathbf {b} )^{2}=\mathbf {a} ^{2}\mathbf {b} ^{2},}$

que utilizando el teorema de Pitágoras, da el valor de (a ∧ b)²

${\displaystyle (\mathbf {a} \wedge \mathbf {b} )^{2}=(\mathbf {a} \cdot \mathbf {b} )^{2}-\mathbf {a} ^{2}\mathbf {b} ^{2}=\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}(\cos ^{2}\theta -1)=-\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}\sin ^{2}\theta }$

Un cuadrado negativo no puede ser una cantidad escalar o vectorial, por lo que es un nuevo tipo de objeto, un bivector. Tiene magnitud | a | | b | | sinθ |, donde θ es el ángulo entre los vectores, y por lo tanto es cero para vectores paralelos.

Para distinguirlos de los vectores, los bivectores se escriben aquí con mayúsculas en negrita, por ejemplo:

${\displaystyle \mathbf {A} =\mathbf {a} \wedge \mathbf {b} =-\mathbf {b} \wedge \mathbf {a} \ ,}$

aunque se utilizan otras convenciones, en particular cuando vectores y bivectores son elementos del álgebra geométrica.

Propiedades

El espacio Λ²ℝⁿ

El álgebra generada por el producto geométrico es el álgebra geométrica sobre el espacio vectorial. Para un espacio vectorial euclídeo se escribe ${\displaystyle {\mathcal {G}}_{n}}$ o Cℓ_n(ℝ), donde n es la dimensión del espacio vectorial ℝⁿ. Cℓ_n es tanto un espacio vectorial como un álgebra, generado por todos los productos entre vectores en ℝⁿ, por lo que contiene todos los vectores y bivectores. Más precisamente, siendo un espacio vectorial, contiene los vectores y bivectores como subespacios vectoriales, aunque no subálgebras (ya que el producto geométrico de dos vectores no es generalmente otro vector). El espacio de todos los bivectores se escribe Λ²ℝⁿ.^[12]

Subálgebra par

La subálgebra generada por los bivectores es la subálgebra par del álgebra geométrica, denotada como Cℓ+
n. Este álgebra resulta de considerar todos los productos de escalares y bivectores generados por el producto geométrico. Tiene la dimensión 2ⁿ⁻¹ y contiene Λ²ℝⁿ como un subespacio lineal con la dimensión 1/2n(n−1) (un número triangular). En dos y tres dimensiones, la subálgebra uniforme contiene solo escalares y bivectores, y cada uno es de particular interés. En dos dimensiones, la subálgebra par es isomórfica a los números complejos, mientras que en tres es isomorfa a los cuaterniones. Más generalmente, la subálgebra uniforme puede usarse para generar rotaciones en cualquier dimensión, y puede ser generada por bivectores en el álgebra.

Magnitud

Como se señaló en la sección anterior, la magnitud de un bivector simple, que es el producto exterior de dos vectores a y b, es |a| |b| sin θ, donde θ es el ángulo entre los vectores. Se escribe |B|, donde B es el bivector.

Para los bivectores generales, la magnitud se puede calcular tomando la norma del bivector considerado como un vector en el espacio Λ²ℝⁿ. Si la magnitud es cero, entonces todas las componentes del bivector son cero, y el bivector es el bivector cero, que como elemento del álgebra geométrica es igual al cero escalar.

Bivectores unidad

Un bivector unidad posee magnitud 1. Se puede construir a partir de cualquier bivector que no sea cero, dividiendo el bivector por su magnitud, es decir

${\displaystyle {\frac {\mathbf {B} }{\left|\mathbf {B} \right|}}.}$

De particular interés son los bivectores unitarios formados a partir de los productos de la base canónica. Si e _i y e _j son vectores de una base distintos entre sí, entonces el producto e_i ∧ e_j es un bivector. Como los vectores son ortogonales, esto es solo e_i e_j, escrito e_ij, con magnitud uno, ya que los vectores son todos unitarios. El conjunto de todos estos bivectores forman una base de Λ²ℝⁿ. Por ejemplo, en cuatro dimensiones, la base de Λ²ℝ⁴ es (e₁ e₂, e₁ e₃, e₁ e₄, e₂ e₃, e₂ e₄, e₃ e₄) o (e₁₂, e₁₃, e₁₄, e₂₃, e₂₄, e₃₄).^[13]

Bivectores simples

El producto exterior de dos vectores es un bivector, pero no todos los bivectores son productos exteriores de dos vectores. Por ejemplo, en cuatro dimensiones el bivector

${\displaystyle \mathbf {B} =\mathbf {e} _{1}\wedge \mathbf {e} _{2}+\mathbf {e} _{3}\wedge \mathbf {e} _{4}=\mathbf {e} _{1}\mathbf {e} _{2}+\mathbf {e} _{3}\mathbf {e} _{4}=\mathbf {e} _{12}+\mathbf {e} _{34}}$

no se puede escribir como el producto exterior de dos vectores. Un bivector que se puede escribir como el producto exterior de dos vectores es simple. En dos y tres dimensiones todos los bivectores son simples, pero no en cuatro o más dimensiones; en cuatro dimensiones, cada bivector es la suma de, como máximo, dos productos exteriores. Un bivector tiene un cuadrado real solo si es simple, y solo los bivectores simples pueden representarse geométricamente mediante un área de plano orientado.^[2]

Producto de dos bivectores

El producto geométrico de dos bivectores, A y B, es

${\displaystyle \mathbf {A} \mathbf {B} =\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} +\mathbf {A} \wedge \mathbf {B} .}$

La cantidad A · B es el producto interior de valor escalar, mientras que A ∧ B es el producto exterior de grado 4 que surge en cuatro o más dimensiones. La cantidad A × B es el producto conmutador de dos operadores de valor bivector, dado por

${\displaystyle \mathbf {A} \times \mathbf {B} ={\frac {1}{2}}(\mathbf {AB} -\mathbf {BA} ),}$^[14]

El espacio de los bivectores Λ²ℝⁿ es un álgebra de Lie sobre ℝ, con el producto del conmutador como el soporte de Lie. El producto geométrico completo de los bivectores genera una subálgebra uniforme.

De particular interés es el producto de un bivector consigo mismo. Como el producto del conmutador es antisimétrico, el producto se simplifica a

${\displaystyle \mathbf {A} \mathbf {A} =\mathbf {A} \cdot \mathbf {A} +\mathbf {A} \wedge \mathbf {A} .}$

Si el bivector es "simple", el último término es cero y el producto A · A es de valor escalar, que se puede usar para verificar la simplicidad. En particular, el producto exterior de los bivectores solo existe en cuatro o más dimensiones, por lo que todos los bivectores en dos y tres dimensiones son simples.^[2]

Dos dimensiones

Cuando se trabaja con coordenadas en álgebra geométrica, es habitual escribir la base como (e₁, e₂, ...), una convención que se usará aquí.

Un vector en el espacio bidimensional real ℝ² se puede escribir como a = a₁e₁ + a₂e₂, donde a₁ y a₂ son dos números reales; y e₁ y e₂ son los vectores de una base ortonormal. El producto geométrico de dos de tales vectores es

${\displaystyle {\begin{aligned}\mathbf {a} \mathbf {b} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2})(b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2})\\&=a_{1}b_{1}\mathbf {e} _{1}\mathbf {e} _{1}+a_{1}b_{2}\mathbf {e} _{1}\mathbf {e} _{2}+a_{2}b_{1}\mathbf {e} _{2}\mathbf {e} _{1}+a_{2}b_{2}\mathbf {e} _{2}\mathbf {e} _{2}\\&=a_{1}b_{1}+a_{2}b_{2}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.\end{aligned}}}$

Esto se puede dividir en el producto interior simétrico, de valor escalar, y un producto exterior antisimétrico, de valor bivectorial:

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2},\\\mathbf {a} \wedge \mathbf {b} &=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12}.\end{aligned}}}$

Todos los bivectores en dos dimensiones son de esta forma, es decir, múltiplos del bivector e₁ e₂, escrito e₁₂ para enfatizar que es un bivector en lugar de un vector. La magnitud de e₁₂ es 1, con

${\displaystyle \mathbf {e} _{12}^{2}=-1,}$

por eso se llama el bivector unidad. El término bivector unidad se puede usar en otras dimensiones, pero solo se define de forma única (hasta el signo) en dos dimensiones y todos los bivectores son múltiplos de e₁₂. Como el elemento de grado más alto del álgebra e₁₂, es también el pseudoscalar que recibe el símbolo i.

Números complejos

Con las propiedades del cuadrado negativo y la magnitud de la unidad, el bivector unidad se puede identificar con la unidad imaginaria de los número complejos. Los bivectores y los escalares forman juntos la subálgebra uniforme del álgebra geométrica, que es un isomorfismo con respecto a los números complejos. El subálgebra par tiene base (1, e₁₂), todo el álgebra tiene base (1, e₁, e₂, e₁₂).

Los números complejos generalmente se identifican con los vectores en coordenadas cartesianas bidimensionales, lo que significaría asociarlos con los elementos vectoriales del álgebra geométrica. No hay ninguna contradicción en esto, ya que para pasar de un vector general a un número complejo, un eje debe identificarse como el eje real, denominado e₁. Esto se multiplica por todos los vectores para generar los elementos del subálgebra par.

Todas las propiedades de los números complejos pueden derivarse de los bivectores, pero dos son de particular interés. En primer lugar, como los números complejos, el producto de bivectores y por lo tanto, la subálgebras pares son conmutativas. Esto solo es cierto en dos dimensiones, por lo que las propiedades del bivector en dos dimensiones que dependen de la conmutatividad no suelen generalizarse a dimensiones más altas.

En segundo lugar, se puede escribir un bivector general como

${\displaystyle \theta \mathbf {e} _{12}=i\theta ,}$

donde θ es un número real. Aplicando la serie de Taylor de la exponencial y usando la propiedad e₁₂² = −1, se obtiene como resultado una versión bivectorial de la fórmula de Euler,

${\displaystyle e^{\theta \mathbf {e} _{12}}=e^{i\theta }=\cos {\theta }+i\sin {\theta },}$

que cuando se multiplica por cualquier vector lo rota en un ángulo θ sobre el origen:

${\displaystyle (x'\mathbf {e} _{1}+y'\mathbf {e} _{2})=(x\mathbf {e} _{1}+y\mathbf {e} _{2})e^{i\theta }.}$

El producto de un vector con un bivector en dos dimensiones es anticonmutativo, por lo que los siguientes productos generan la misma rotación:

${\displaystyle \mathbf {v} '=\mathbf {v} e^{i\theta }=e^{-i\theta }\mathbf {v} =e^{\frac {-i\theta }{2}}\mathbf {v} e^{\frac {i\theta }{2}}.}$

De estos, el último producto es el que se generaliza en dimensiones más altas. La cantidad necesaria se llama rotor y recibe el símbolo R, por lo que en dos dimensiones se puede escribir un rotor que gire el ángulo θ como:

${\displaystyle R=e^{\frac {-i\theta }{2}}=e^{\frac {-\theta \mathbf {e} _{12}}{2}},}$

y la rotación que genera es:^[15]

${\displaystyle \mathbf {v} '=R\mathbf {v} R^{-1}.\,}$

Tres dimensiones

En tres dimensiones el producto geométrico de dos vectores es:

${\displaystyle {\begin{aligned}\mathbf {ab} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3})(b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+b_{3}\mathbf {e} _{3})\\&=a_{1}b_{1}{\mathbf {e} _{1}}^{2}+a_{2}b_{2}{\mathbf {e} _{2}}^{2}+a_{3}b_{3}{\mathbf {e} _{3}}^{2}+(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{2}\mathbf {e} _{3}+(a_{3}b_{1}-a_{1}b_{3})\mathbf {e} _{3}\mathbf {e} _{1}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.\end{aligned}}}$

Esto se puede dividir en el producto simétrico, de valor escalar, interior; y en el producto antisimétrico, de valor bivector, exterior:

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\\\mathbf {a} \wedge \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{23}+(a_{3}b_{1}-a_{1}b_{3})\mathbf {e} _{31}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12}.\end{aligned}}}$

En tres dimensiones, todos los bivectores son simples y, por lo tanto, el resultado de un producto exterior. Los bivectores unitarios e₂₃, e₃₁ y e₁₂ forman una base del espacio de los bivectores Λ²ℝ³, que en sí es un espacio lineal tridimensional. Así que si un bivector general es:

${\displaystyle \mathbf {A} =A_{23}\mathbf {e} _{23}+A_{31}\mathbf {e} _{31}+A_{12}\mathbf {e} _{12},}$

se pueden agregar como vectores

${\displaystyle \mathbf {A} +\mathbf {B} =(A_{23}+B_{23})\mathbf {e} _{23}+(A_{31}+B_{31})\mathbf {e} _{31}+(A_{12}+B_{12})\mathbf {e} _{12}.}$

mientras que cuando se multiplican producen lo siguiente:

${\displaystyle \mathbf {A} \mathbf {B} =-A_{23}B_{23}-A_{31}B_{31}-A_{12}B_{12}+(A_{12}B_{31}-A_{31}B_{12})\mathbf {e} _{23}+(A_{23}B_{12}-A_{12}B_{23})\mathbf {e} _{31}+(A_{31}B_{23}-A_{23}B_{31})\mathbf {e} _{12}}$

que se puede dividir en sus partes escalar y bivectorial (antisimétrica y simétrica) de la siguiente manera

${\displaystyle {\begin{aligned}\mathbf {A} \cdot \mathbf {B} &=-A_{12}B_{12}-A_{31}B_{31}-A_{23}B_{23}\\\mathbf {A} \times \mathbf {B} &=(A_{23}B_{31}-A_{31}B_{23})\mathbf {e} _{12}+(A_{12}B_{23}-A_{23}B_{12})\mathbf {e} _{13}+(A_{31}B_{12}-A_{12}B_{31})\mathbf {e} _{23}.\end{aligned}}}$

El producto exterior de dos bivectores en tres dimensiones es cero.

Un bivector B puede escribirse como el producto de su magnitud y un bivector unitario, por lo que se escribe β para |B| y utilizando la serie de Taylor para la exponencial se puede demostrar que

${\displaystyle e^{\mathbf {B} }=e^{\beta {\frac {\mathbf {B} }{\beta }}}=\cos {\beta }+{\frac {\mathbf {B} }{\beta }}\sin {\beta }.}$

Esta es otra versión de la fórmula de Euler, pero con un bivector general en tres dimensiones. A diferencia del caso en dos dimensiones, los bivectores no son conmutativos, por lo que las propiedades que dependen de la conmutatividad no se aplican en tres dimensiones. Por ejemplo, en general e^{A + B} ≠ e^Ae^B en tres (o más) dimensiones.   El álgebra geométrica completa en tres dimensiones, Cℓ₃(ℝ), tiene base (1, e₁, e₂, e₃, e₂₃, e₃₁, e₁₂, e₁₂₃). El elemento e₁₂₃ es un trivector y el pseudoscalar de la geometría. Los bivectores en tres dimensiones a veces se identifican con los vectores axiales^[16] con los que están relacionados, como se analiza más adelante.

Cuaterniones

Los bivectores no están cerrados bajo el producto geométrico, pero la subálgebra es uniforme. En tres dimensiones, consta de todos los elementos escalares y bivectores del álgebra geométrica, por lo que se puede escribir un elemento general, por ejemplo, a+A, donde a es la parte escalar y A es la parte bivector. Está escrito en Cℓ+
3 y tiene base (1, e₂₃, e₃₁, e₁₂). El producto de dos elementos generales de la subálgebra par es

${\displaystyle (a+\mathbf {A} )(b+\mathbf {B} )=ab+a\mathbf {B} +b\mathbf {A} +\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} .}$

La subálgebra par, que es el álgebra que consta de escalares y bivectores, es isomorfa a los cuaterniones, ℍ. Esto se puede ver comparando la base con la base de los cuaterniones, o del producto visto anteriormente, que es idéntico al producto de cuaterniones, excepto por un cambio de signo que se relaciona con los productos negativos en el producto interior bivectorial A · B. Otras propiedades del cuaternión pueden relacionarse de manera similar o derivarse del álgebra geométrica.

Esto sugiere que la división habitual de un cuaternión en partes escalares y vectoriales se representaría mejor como una división en partes escalares y bivectoriales. Si se aplica este criterio, el producto de cuaterniones es simplemente el producto geométrico. También relaciona los cuaterniones en tres dimensiones con los números complejos en dos, ya que cada uno es isomorfo a la subálgebra par de la dimensión correspondiente, una relación que se generaliza a dimensiones más altas.

Vector de rotación

El vector de rotación, la representación axial-angular de un giro, es una forma compacta de representar rotaciones en tres dimensiones. En su forma más compacta, consiste en un vector, el producto de un vector unitario ω que es el eje de rotación con el ángulo (con su signo) de rotación θ, de modo que la magnitud del vector de rotación general θω es igual al ángulo de rotación (sin signo).

El cuaternión asociado a la rotación es:

${\displaystyle q=\left(\cos \left({\frac {\theta }{2}}\right),\omega \sin \left({\frac {\theta }{2}}\right)\right)}$

En álgebra geométrica la rotación está representada por un bivector. Esto se puede ver en su relación con los cuaterniones. Sea Ω un bivector en el plano de rotación, y sea θ el ángulo de rotación. Entonces, el bivector de rotación es Ωθ. El cuaternión se corresponde estrechamente con la exponencial de la mitad del bivector Ωθ. Es decir, los componentes del cuaternión corresponden a las partes escalares y bivectoriales de la siguiente expresión:

${\displaystyle e^{\frac {\Omega \theta }{2}}=\cos \left({\frac {\theta }{2}}\right)+\Omega \sin \left({\frac {\theta }{2}}\right)}$

El exponencial se puede definir en términos de sus series de potencias y se puede evaluar fácilmente utilizando el hecho de que Ω al cuadrado es -1.

Así, las rotaciones pueden ser representadas por bivectores. De la misma forma, los cuaterniones son elementos del álgebra geométrica, y están relacionados por la aplicación exponencial en ese álgebra.

Rotores

El bivector Ωθ genera una rotación a través de la aplicación exponencial. Los elementos pares generados hacen girar un vector general en tres dimensiones de la misma manera que los cuaterniones:

${\displaystyle \mathbf {v} '=e^{\frac {{\boldsymbol {\Omega }}\theta }{2}}\mathbf {v} e^{-{\frac {{\boldsymbol {\Omega }}\theta }{2}}}.}$

En cuanto al caso en dos dimensiones, la cantidad e^Ωθ se llama rotor y se escribe R. La cantidad e^−Ωθ es entonces R⁻¹, y genera las rotaciones de la siguiente manera

${\displaystyle \mathbf {v} '=R\mathbf {v} R^{-1}.\,}$

Esto es idéntico al caso de dos dimensiones, excepto que aquí los rotores son objetos de cuatro dimensiones isomorfos a los cuaterniones. Esto puede generalizarse a todas las dimensiones, con rotores, elementos de la subálgebra par con magnitud uno, generados por la aplicación exponencial de los bivectores. Forman un recubrimiento doble sobre el grupo de rotación, por lo que los rotores R y -R representan la misma rotación.

Matrices

Los bivectores son isomorfos a las matrices antisimétricas. El bivector general B₂₃e₂₃ + B₃₁e₃₁ + B₁₂e₁₂ se corresponde con la matriz.

${\displaystyle M_{B}={\begin{pmatrix}0&B_{12}&-B_{31}\\-B_{12}&0&B_{23}\\B_{31}&-B_{23}&0\end{pmatrix}}.}$

Esto, multiplicado por vectores en ambos lados, da el mismo vector que el producto de un vector y un bivector menos el producto externo. Un ejemplo es el caso de la velocidad angular.

Las matrices antisimétricas generan matrices ortogonales con determinante 1 a través de la aplicación exponencial. En particular, el exponente de un bivector asociado con una rotación es una matriz de rotación, es decir, la matriz de rotación M_R dada por la matriz antisimétrica anterior es:

${\displaystyle M_{R}=e^{M_{B}}.}$

La rotación descrita por M_R es la misma que la descrita por el rotor R dada por:

${\displaystyle R=e^{\frac {B}{2}},}$

y la matriz M_R también se puede calcular directamente desde el rotor R:

${\displaystyle M_{R}={\begin{pmatrix}(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{1}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{2}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{3}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{3}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{3}\end{pmatrix}}.}$

Los bivectores están relacionados con los valores propios de una matriz de rotación. Dada una matriz de rotación M, los valores propios pueden calcularse resolviendo la ecuación característica para esa matriz 0 = det(M − λI). Por el teorema fundamental del álgebra este polinomio posee tres raíces, pero solo una raíz real, ya que solo hay un vector propio, el eje de rotación. Las otras raíces deben ser un par conjugado complejo. Tienen magnitud unidad, tratándose de logaritmos imaginarios puros, iguales a la magnitud del bivector asociado con la rotación, que también es el ángulo de rotación. Los vectores propios asociados con los valores propios complejos están en el plano del bivector, por lo que el producto exterior de dos vectores propios no paralelos da como resultado el bivector, o al menos un múltiplo de él.

Vectores axiales

El momento 3-angular es un bivector (elemento plano) y un vector axial, de una partícula de masa m con 3-posición instantánea x y 3-momento p

El vector de rotación es un ejemplo de un vector axial. Los vectores axiales, o pseudovectores, son vectores con la característica especial de que sus coordenadas experimentan un cambio de signo en relación con los vectores habituales (también llamados vectores polares) que se invierten a través del origen, la reflexión en un plano u otra transformación lineal con inversión de orientación.^[17] Los ejemplos incluyen magnitudes como el par motor, el momento angular y el vector del campo magnético. Las cantidades que utilizan vectores axiales en el álgebra vectorial están representadas adecuadamente por bivectores en el álgebra geométrica.^[18] Más precisamente, si se elige una orientación subyacente, los vectores axiales se identifican naturalmente con los vectores habituales. El dual de Hodge proporciona un isomorfismo entre los vectores axiales y los bivectores, por lo que cada vector axial está asociado con un bivector y viceversa; es decir:

${\displaystyle \mathbf {A} =*\mathbf {a} \,,\quad \mathbf {a} =*\mathbf {A} }$

donde ∗ indica el dual de Hodge. Tenga en cuenta que si la orientación subyacente se invierte por inversión a través del origen, tanto la identificación de los vectores axiales con los vectores habituales como el signo de cambio dual de Hodge, pero los bivectores no se mueven. Alternativamente, usando el pseudoscalar unidad en Cℓ₃ (ℝ), i=e₁, e₂, e₃ da

${\displaystyle \mathbf {A} =\mathbf {a} i\,,\quad \mathbf {a} =-\mathbf {A} i.}$

Esta forma es más fácil de usar, ya que el producto es solo el producto geométrico. Pero es antisimétrico porque (como en dos dimensiones) la unidad pseudoscalar i se ajusta a −1, por lo que se necesita introducir un valor negativo en uno de los productos.

Esta relación se extiende a operaciones como el vector producto vectorial con valor vectorial y el producto exterior con valor de bivector, ya que cuando se escriben como determinantes se calculan de la misma manera:

${\displaystyle \mathbf {a} \times \mathbf {b} ={\begin{vmatrix}\mathbf {e} _{1}&\mathbf {e} _{2}&\mathbf {e} _{3}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\,,\quad \mathbf {a} \wedge \mathbf {b} ={\begin{vmatrix}\mathbf {e} _{23}&\mathbf {e} _{31}&\mathbf {e} _{12}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\ ,}$

Así están relacionados por el dual de Hodge:

${\displaystyle {*(\mathbf {a} \wedge \mathbf {b} )}=\mathbf {a\times b} \,,\quad {*(\mathbf {a\times b} )}=\mathbf {a} \wedge \mathbf {b} .}$

Los bivectores tienen una serie de ventajas sobre los vectores axiales. Se diferencian mejor los vectores axiales y polares, es decir, las cantidades representadas por ellos, por lo que es más claro qué operaciones están permitidas y cuáles son sus resultados. Por ejemplo, el producto interno de un vector polar y un vector axial que resulta del producto cruzado en el producto mixto debe dar como resultado un pseudoscalar, un resultado que es más obvio si el cálculo se enmarca como el producto exterior de un vector y un bivector. Se generalizan a otras dimensiones; en particular, los bivectores se pueden usar para describir cantidades como el par y el momento angular en dos y en tres dimensiones. Además, coinciden estrechamente con la intuición geométrica de varias maneras, como se ve en la siguiente sección.^[19]

Interpretación geométrica

Como sugieren su nombre y el del álgebra, uno de los atractivos de los bivectores es que tienen una interpretación geométrica natural. Esto se puede describir en cualquier dimensión, pero es mejor hacerlo en tres, donde se pueden establecer paralelismos con objetos más familiares, antes de aplicarlos a dimensiones más altas. En dos dimensiones, la interpretación geométrica es trivial, ya que el espacio es bidimensional, por lo que tiene solo un plano, y todos los bivectores están asociados con él, diferenciándose solo por un factor de escala.

Todos los bivectores pueden interpretarse como planos, o más precisamente como sectores planos orientados. En tres dimensiones hay tres propiedades de un bivector que pueden ser interpretadas geométricamente:

• La disposición del plano en el espacio, precisamente la disposición del plano (o alternativamente, su rotación, orientación geométrica o gradiente del plano), se asocia con la relación de los componentes del bivector. En particular, los tres bivectores básicos, e₂₃,e₃₁ y e₁₂, o múltiplos escalares de ellos, están asociados con el plano yz, el plano xz y el plano xy respectivamente.
• La magnitud del bivector está asociado con el área del sector plano. El área no tiene una forma particular, por lo que se puede utilizar cualquier forma. Incluso se puede representar de otras maneras, como por ejemplo una medida angular. Pero si los vectores se interpretan como longitudes, el bivector generalmente se interpreta como un área con las mismas unidades, de la manera siguiente:
• Al igual que la dirección de un vector, un plano asociado con un bivector tiene una dirección, una circulación o un sentido de rotación en el plano, que toma dos valores (positivo o negativo) en relación con el sentido del reloj cuando se observa desde un punto de vista no contenido en el plano. Esto se asocia con un cambio de signo en el bivector, es decir, si se invierte la dirección, cambia el signo del bivector. Alternativamente, si dos bivectores tienen la misma disposición y magnitud pero direcciones opuestas, uno es el negativo del otro.
• Si se imagina como un paralelogramo 2d, con el origen del vector en 0, el área (con su signo) es el determinante de las coordenadas cartesianas de los vectores (${\displaystyle a_{x}b_{y}-b_{x}a_{y}}$).^[20]

El producto cruzado a × b es ortogonal al bivector a ∧ b

En tres dimensiones, todos los bivectores pueden ser generados por el producto exterior de dos vectores. Si el bivector B = a ∧ b, entonces la magnitud de B es

${\displaystyle \left|\mathbf {B} \right|=\left|\mathbf {a} \right|\left|\mathbf {b} \right|\sin {\theta },}$

donde θ es el ángulo entre los vectores. Esta es el área del paralelogramo con lados a y b, como se muestra en el diagrama. Una interpretación es que el área es barrida por b a medida que avanza a. El producto exterior es antisimétrico, por lo que invertir el orden de a y b para hacer que a se mueva en b resulta en un bivector con el Dirección opuesta que es la negativa de la primera. El plano del bivector a ∧ b contiene tanto a a como a b, por lo que ambos son paralelos al plano.

Los bivectores y vectores axiales están relacionados por la dualidad de Hodge. En un espacio vectorial real, el dual de Hodge relaciona un subespacio con su complemento ortogonal, por lo que si un bivector está representado por un plano, el vector axial asociado con él es simplemente el vector normal del plano. El plano tiene dos normales, una en cada lado, que determinan las dos orientaciones relativas posibles entre el plano y el bivector.

Relación entre fuerza F, torsor τ, cantidad de movimiento p y momento angular L

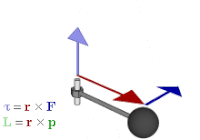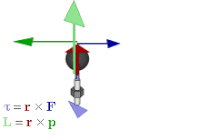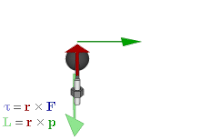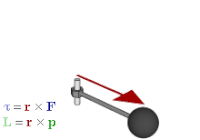
Este hecho relaciona el producto vectorial con el producto exterior. También se puede utilizar para representar cantidades físicas, como par motor y momento angular. En el álgebra vectorial, generalmente se representan mediante vectores, perpendiculares al plano en el que se definen la fuerza, la cantidad de movimiento o el desplazamiento. Pero si se usa un bivector en su lugar, el plano es el plano del bivector, por lo que es una forma más natural de representar las cantidades y la forma en que actúan. A diferencia de la representación vectorial, también se generaliza en otras dimensiones.

El producto de dos bivectores tiene una interpretación geométrica. Para los bivectores que no sean cero A y B, el producto se puede dividir en partes simétricas y antisimétricas de la siguiente manera:

${\displaystyle \mathbf {AB} =\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} .}$

Al igual que los vectores, estos tienen magnitudes | A · B | = | A || B | cos θ y | A × B | = | A || B | sin θ, donde θ es el ángulo entre los planos. En tres dimensiones es el mismo que el ángulo entre los vectores normales duales a los planos, y se generaliza en cierta medida en dimensiones más altas.

Dos bivectores, coincidentes con dos de las caras no paralelas de un prisma, siendo sumadas para generar un tercer bivector^[12]

Los bivectores se pueden sumar como áreas. Dados dos bivectores que no son cero B y C en tres dimensiones, siempre es posible encontrar un vector a que esté contenido en ambos, por lo que los bivectores se pueden definir como productos exteriores que implican a a:

${\displaystyle {\begin{aligned}\mathbf {B} &=\mathbf {a} \wedge \mathbf {b} \\\mathbf {C} &=\mathbf {a} \wedge \mathbf {c} \end{aligned}}}$

Esto se puede interpretar geométricamente como se ve en el diagrama: las dos áreas se suman para dar una tercera, con las tres áreas formando las caras de un prisma con a, b, c y b + c como aristas. Esto corresponde a las dos formas de calcular el área utilizando la distributividad del producto exterior:

${\displaystyle {\begin{aligned}\mathbf {B} +\mathbf {C} &=\mathbf {a} \wedge \mathbf {b} +\mathbf {a} \wedge \mathbf {c} \\&=\mathbf {a} \wedge (\mathbf {b} +\mathbf {c} ).\end{aligned}}}$

Esta propiedad solo se verifica en tres dimensiones, ya que es la única dimensión donde debe existir un vector paralelo a ambos bivectores. En dimensiones más altas, los bivectores generalmente no están asociados con un solo plano, o si lo son (bivectores simples), es posible que dos bivectores no tengan un vector en común, por lo que se suman en un bivector no simple.

Cuatro dimensiones

En cuatro dimensiones, los elementos básicos del espacio Λ²ℝ⁴ de los bivectores son (e₁₂, e₁₃, e₁₄, e₂₃, e₂₄, e₃₄), por lo que un bivector general es de la forma

${\displaystyle \mathbf {A} =a_{12}\mathbf {e} _{12}+a_{13}\mathbf {e} _{13}+a_{14}\mathbf {e} _{14}+a_{23}\mathbf {e} _{23}+a_{24}\mathbf {e} _{24}+a_{34}\mathbf {e} _{34}.}$

Ortogonalidad

En cuatro dimensiones, el dual de Hodge de un bivector es otro bivector, y el espacio Λ²ℝ⁴ es dual a sí mismo. Los vectores normales no son únicos, pero en cambio, cada plano es ortogonal a todos los vectores en su espacio dual de Hodge, lo que se puede usar para dividir los bivectores en dos mitades de la siguiente manera: sean tres pares de bivectores ortogonales: (e₁₂, e₃₄), (e₁₃, e₂₄) y (e₁₄, e₂₃). Hay cuatro formas distintas de elegir un bivector de cada uno de los dos primeros pares, y una vez que se seleccionan estos dos primeros, su suma produce el tercer bivector del otro par. Por ejemplo, (e₁₂, e₁₃, e₁₄) y (e₂₃, e₂₄ , e₃₄).

Bivectores simples en 4D

En cuatro dimensiones, los bivectores son generados por el producto exterior de los vectores en ℝ⁴, pero con una diferencia importante con respecto a ℝ³ y a ℝ², dado que en cuatro dimensiones no todos los bivectores son simples. Por ejemplo, hay bivectores como e₁₂ + e₃₄ que no pueden ser generados por el producto exterior de dos vectores. Esto también significa que no tienen un cuadrado real, es decir, escalar. En este caso

${\displaystyle (\mathbf {e} _{12}+\mathbf {e} _{34})^{2}=\mathbf {e} _{12}\mathbf {e} _{12}+\mathbf {e} _{12}\mathbf {e} _{34}+\mathbf {e} _{34}\mathbf {e} _{12}+\mathbf {e} _{34}\mathbf {e} _{34}=-2+2\mathbf {e} _{1234}.}$

El elemento e₁₂₃₄ es el pseudoscalar en Cℓ₄ (distinto de un escalar propiamente dicho), por lo que el cuadrado no es escalar.

Todos los bivectores en cuatro dimensiones se pueden generar utilizando como máximo dos productos exteriores y cuatro vectores. El bivector anterior se puede escribir como

${\displaystyle \mathbf {e} _{12}+\mathbf {e} _{34}=\mathbf {e} _{1}\wedge \mathbf {e} _{2}+\mathbf {e} _{3}\wedge \mathbf {e} _{4}.}$

De manera similar, cada bivector se puede escribir como la suma de dos bivectores simples. Es útil elegir dos bivectores ortogonales para esto, y siempre es posible hacerlo. Además, para un bivector genérico, la elección de los bivectores simples es única, es decir, solo hay una forma de descomposición en bivectores ortogonales; la única excepción es cuando los dos bivectores ortogonales tienen magnitudes iguales (como en el ejemplo anterior): en este caso, la descomposición no es única.^[2] La descomposición es siempre única en el caso de los bivectores simples, con la ventaja añadida de que una de las partes ortogonales es cero.

Rotaciones en ℝ⁴

Como en tres dimensiones, los bivectores en cuatro dimensiones generan rotaciones a través de la aplicación exponencial, y todas las rotaciones se pueden generar de esta manera. Como en tres dimensiones, si B es un bivector, el rotor R es e^B/2 y las rotaciones se generan de la misma manera:

${\displaystyle v'=RvR^{-1}.\,}$

Proyección 3D de un teseracto sometido a una rotación isoclinica

Sin embargo, las rotaciones generadas son más complejas. Se pueden categorizar de la siguiente manera:

Las rotaciones simples son aquellas que fijan un plano en 4D y giran en un ángulo sobre este plano.

Las rotaciones dobles tienen solo un punto fijo, el origen, y giran en dos ángulos alrededor de dos planos ortogonales. En general, los ángulos son diferentes y los planos están especificados explícitamente.

Las rotaciones isoclínicas son rotaciones dobles donde los ángulos de rotación son iguales. En este caso, los planos sobre los que se lleva a cabo la rotación no son únicos.

Estas rotaciones son generadas por bivectores de una manera directa. Las rotaciones simples se generan mediante bivectores simples, con el plano fijo dual u ortogonal al plano del bivector. Se puede decir que la rotación tiene lugar alrededor de ese plano, en el plano del bivector. Todos los otros bivectores generan rotaciones dobles, con los dos ángulos de rotación igualando las magnitudes de los dos bivectores simples de los que se compone el bivector no simple. Las rotaciones isoclínicas surgen cuando estas magnitudes son iguales, en cuyo caso la descomposición en dos bivectores simples no es única.^[21]

Los bivectores en general no conmutan, pero una excepción son los bivectores ortogonales y sus exponenciales. Entonces, si el bivector B = B₁ + B₂, donde B₁ y B₂ son bivectores ortogonales simples, se puede utilizar para generar una rotación que se descompone en dos rotaciones simples que conmutan de la siguiente manera:

${\displaystyle R=e^{\frac {\mathbf {B} _{1}+\mathbf {B} _{2}}{2}}=e^{\frac {\mathbf {B} _{1}}{2}}e^{\frac {\mathbf {B} _{2}}{2}}=e^{\frac {\mathbf {B} _{2}}{2}}e^{\frac {\mathbf {B} _{1}}{2}}}$

lo que siempre es posible, ya que todos los bivectores se pueden expresar como sumas de bivectores ortogonales.

Rotaciones en el espacio-tiempo

El espacio-tiempo es un modelo matemático del universo utilizado en la relatividad especial. Contempla las tres dimensiones del espacio y una dimensión temporal, combinadas en un solo espacio de cuatro dimensiones. Se describe naturalmente utilizando el álgebra geométrica y los bivectores, con la distancia euclidiana reemplazada por el espacio-tiempo de Minkowski. Esta álgebra es idéntica a la del espacio euclídeo, excepto que se cambia la signatura, por lo que

${\displaystyle {\mathbf {e} _{i}}^{2}={\begin{cases}1,&i=1,2,3\\-1,&i=4\end{cases}}}$

(téngase en cuenta que el orden y los índices anteriores no son universales, aquí e₄ es la dimensión temporal). El álgebra geométrica es Cℓ_3,1(ℝ), y el subespacio de los bivectores es Λ²ℝ^3,1.

Los bivectores simples son de dos tipos. Los bivectores simples e₂₃, e₃₁ y e₁₂ tienen cuadrados negativos y abarcan los bivectores del subespacio tridimensional correspondiente al espacio euclidiano, ℝ³. Estos bivectores generan rotaciones ordinarias en ℝ³.

Los bivectores simples e₁₄, e₂₄ y e₃₄ tienen cuadrados positivos y, como planos, abarcan una dimensión espacial y la dimensión temporal. Estos también generan rotaciones a través de la aplicación exponencial, pero en lugar de funciones trigonométricas, se necesitan funciones hiperbólicas, que generan un rotor de la siguiente manera:

${\displaystyle e^{\frac {{\boldsymbol {\Omega }}\theta }{2}}=\cosh \left({\frac {\theta }{2}}\right)+{\boldsymbol {\Omega }}\sinh \left({\frac {\theta }{2}}\right),}$

donde Ω es el bivector (e₁₄, etc.), identificado a través de la métrica con una transformación lineal antisimétrica de ℝ^3,1. Estos son los impulsos de Lorentz, expresados de una manera particularmente compacta, utilizando el mismo tipo de álgebra que en ℝ³ y ℝ⁴.

En general, todas las rotaciones del espacio-tiempo se generan desde los bivectores a través de la aplicación exponencial, es decir, un rotor general generado por el bivector A tiene la forma

${\displaystyle R=e^{\frac {\mathbf {A} }{2}}.}$

El conjunto de todas las rotaciones en el espacio-tiempo forma el grupo de Lorentz, y de ellas se pueden deducir la mayoría de las consecuencias de la relatividad especial. De manera más general, se demuestra cómo se pueden describir las transformaciones en el espacio euclidiano y el espacio-tiempo utilizando el mismo tipo de álgebra.

Ecuaciones de Maxwell

(Nota: en esta sección, los 3 vectores tradicionales se indican mediante líneas sobre los símbolos, y el vector del espacio-tiempo y los bivectores con símbolos en negrita, con los vectores J y A excepcionalmente en mayúsculas)

Las ecuaciones de Maxwell se utilizan en física para describir la relación entre los campos eléctrico y magnético. Normalmente dados como cuatro ecuaciones diferenciales, tienen una forma especialmente compacta cuando los campos se expresan como un bivector de espacio-tiempo de Λ²ℝ^3,1. Si los campos eléctrico y magnético en ℝ³ son E y B, entonces el bivector electromagnético es

${\displaystyle \mathbf {F} ={\frac {1}{c}}{\overline {E}}\mathbf {e} _{4}+{\overline {B}}\mathbf {e} _{123},}$

donde e₄ es nuevamente el vector base para la dimensión temporal y c es la velocidad de la luz. El producto B e₁₂₃ produce el bivector que es dual de Hodge para B en tres dimensiones, como discussed above, mientras que E e₄ como producto de vectores ortogonales también tiene un valor de bivector. En general, es el tensor de campo electromagnético expresado de forma más compacta como un bivector, y se utiliza de la siguiente manera. Primero se relaciona con la cuadricorriente J, una cantidad vectorial dada por

${\displaystyle \mathbf {J} ={\overline {j}}+c\rho \mathbf {e} _{4},}$

donde j es la densidad de corriente y ρ es la carga eléctrica. Están relacionados por un operador diferencial ∂, que es

${\displaystyle \partial =\nabla -\mathbf {e} _{4}{\frac {1}{c}}{\frac {\partial }{\partial t}}.}$

El operador ∇ es un operador diferencial en álgebra geométrica, actuando sobre las dimensiones del espacio y dado por ∇M = ∇·M + ∇∧M. Cuando se aplica a los vectores ∇ · M es la divergencia y ∇∧ M es el rotacional pero con un bivector en lugar de un vector, esto es dual en tres dimensiones al rotacional. Para la cantidad general M, actúan como reductores de grado y elevando operadores diferenciales. En particular, si M es un escalar, entonces este operador es solo el gradiente, y puede considerarse como un operador nabla algebraico geométrico.

Juntos, pueden usarse para dar una forma particularmente compacta a las ecuaciones de Maxwell en el vacío:

${\displaystyle \partial \mathbf {F} =\mathbf {J} .}$

Cuando se descompone de acuerdo con el álgebra geométrica, el uso de productos geométricos que tienen efectos de aumento de grado y de disminución de grado, es equivalente a las cuatro ecuaciones de Maxwell. Esta es su forma en el vacío, pero la forma general es solo un poco más compleja. También está relacionada con el cuatro-potencial electromagnético, un vector A dado por

${\displaystyle \mathbf {A} ={\overline {A}}+{\frac {1}{c}}V\mathbf {e} _{4},}$

donde A es el potencial magnético vectorial y V es el potencial eléctrico. Se relaciona con el bivector electromagnético de la siguiente manera

${\displaystyle \partial \mathbf {A} =-\mathbf {F} ,}$

utilizando el mismo operador diferencial ∂.^[22]

Dimensiones superiores

Como se ha sugerido en secciones anteriores, gran parte del álgebra geométrica se generaliza bien en dimensiones más altas. El álgebra geométrica para el espacio real ℝⁿ es Cℓ_n (ℝ), y el subespacio de los bivectores es Λ²ℝⁿ.

El número de bivectores simples necesarios para formar un bivector general aumenta con la dimensión, por lo que para n impar es (n−1)/2 y para n par es n/2. Por lo tanto, para las cuatro y cinco dimensiones solo se necesitan dos bivectores simples, pero se requieren tres para la sexta y la séptima dimensiones. Por ejemplo, en seis dimensiones con base estándar (e ₁, e₂, e₃, e₄, e₅,e₆) el bivector

${\displaystyle \mathbf {e} _{12}+\mathbf {e} _{34}+\mathbf {e} _{56}}$

es la suma de tres bivectores simples, pero no menos. Como en cuatro dimensiones, siempre es posible encontrar bivectores ortogonales simples para esta suma.

Rotaciones en dimensiones superiores

Como los rotores de tres y cuatro dimensiones son generados por la aplicación exponencial, así

${\displaystyle e^{\frac {\mathbf {B} }{2}}}$

es el rotor generado por el bivector B. Las rotaciones simples, que tienen lugar en un plano de rotación alrededor de una hoja fija de dimensión (n − 2), son generadas por bivectores simples, mientras que otros bivectores generan rotaciones más complejas que pueden describirse a su vez en términos de sumas de bivectores simples, cada una relacionada con un plano de rotación. Todos los bivectores se pueden expresar como la suma de bivectores ortogonales y conmutativos simples, por lo que las rotaciones siempre se pueden descomponer en un conjunto de rotaciones conmutativas sobre los planos asociados con estos bivectores. El grupo de rotores en n dimensiones forma el grupo espinorial, Espín(n).

Una característica notable, relacionada con el número de bivectores simples y, por lo tanto, de los planos de rotación, es que en las dimensiones impares, cada rotación tiene un eje fijo; es engañoso llamarlo un eje de rotación, ya que en las dimensiones más altas las rotaciones tienen lugar en múltiples planos ortogonales, lo que se relaciona con los bivectores, ya que los bivectores en dimensiones impares se descomponen en el mismo número de bivectores que la dimensión par por debajo, por lo que tienen el mismo número de planos, pero una dimensión adicional. Como cada plano genera rotaciones en dos dimensiones en dimensiones impares, debe haber una dimensión, es decir, un eje invariante, que no se está rotando.^[23]

Los bivectores también están relacionados con las matrices de rotación en n dimensiones. Como en tres dimensiones, el polinomio característico de una matriz se puede resolver para encontrar sus valores propios. En dimensiones impares, presenta al menos una raíz real (siendo el autovector el eje fijo de rotación), y en dimensiones pares no tiene raíces reales, por lo que todas o todas menos una de las raíces son pares complejos conjugados. Cada par está asociado con un componente simple del bivector asociado con la rotación. En particular, el registro de cada par es ± la magnitud, mientras que los vectores propios generados a partir de las raíces son paralelos y, por lo tanto, se pueden usar para generar el bivector. En general, los valores propios y los bivectores son únicos, y el conjunto de valores propios proporciona la descomposición completa en bivectores simples; si las raíces se repiten, la descomposición del bivector en bivectores simples no es única.

Geometría proyectiva

El álgebra geométrica se puede aplicar a la geometría proyectiva de una manera directa. El álgebra geométrica utilizada es Cℓ_n(ℝ), n ≥ 3, el álgebra del espacio vectorial real ℝⁿ, que se utiliza para describir objetos en el espacio proyectivo real ℝℙ^{n − 1}. Los vectores que no son cero en Cℓ_n(ℝ) o ℝⁿ están asociados con puntos en el espacio proyectivo, por lo que los vectores que se diferencian solo por un factor de escala, su producto exterior es cero y se asignan al mismo punto. Los bivectores simples que no son cero en Λ²ℝⁿ representan líneas en ℝℙ^{n − 1}, con bivectores que difieren solo por un factor de escala (positivo o negativo) que representa la misma recta.

Una descripción de la geometría proyectiva se puede construir en el álgebra geométrica usando operaciones básicas. Por ejemplo, dados dos puntos distintos en ℝℙⁿ⁻¹ representados por los vectores a y b, la recta entre ellos está dada por a ∧ b (o b ∧ a). Dos rectas se intersecan en un punto si A ∧ B = 0 para sus bivectores A y B. Este punto está dado por el vector

${\displaystyle \mathbf {p} =\mathbf {A} \lor \mathbf {B} =(\mathbf {A} \times \mathbf {B} )J^{-1}.}$

La operación "⋁" es la confluencia, que se puede definir como anteriormente en términos de la unión, J = A ∧ B para A ∧ B no cero. Usando estas operaciones, la geometría proyectiva se puede formular en términos de álgebra geométrica. Por ejemplo, dado un tercer bivector C (distinto de cero), el punto p se encuentra en la recta dada por C si y solo si

${\displaystyle \mathbf {p} \land \mathbf {C} =0.}$

Así que la condición para las rectas dadas por A, B y C sean colineales es que

${\displaystyle (\mathbf {A} \lor \mathbf {B} )\land \mathbf {C} =0,}$

lo que en Cℓ₃(ℝ) y ℝℙ² se simplifica a

${\displaystyle \langle \mathbf {ABC} \rangle =0,}$

donde los corchetes de ángulo denotan la parte escalar del producto geométrico. De la misma manera, todas las operaciones del espacio proyectivo se pueden escribir en términos de álgebra geométrica, con los bivectores que representan rectas generales en el espacio proyectivo, por lo que toda la geometría se puede desarrollar utilizando el álgebra geométrica.^[14]

Tensores y matrices

Como ya se ha visto, un bivector se puede escribir como una matriz antisimétrica, que a través de la aplicación exponencial genera una matriz de rotación que describe la misma rotación que el rotor, también generado por la aplicación exponencial pero aplicada al vector. Pero también se utiliza con otros bivectores, como el de la velocidad angular y el tensor de campo electromagnético, respectivamente una matriz o un tensor antisimétricos de 3 × 3 y de 4 × 4.

Los bivectores reales en Λ²ℝⁿ son isomorfos a matrices antisimétricas de orden nxn, o alternativamente, a tensores antisimétricos de orden 2 en ℝⁿ. Si bien los bivectores son isomorfos a los vectores (a través del dual) en tres dimensiones, pueden representarse mediante matrices antisimétricas en cualquier dimensión. Esto es útil para relacionar los bivectores con los problemas descritos por las matrices, por lo que se pueden volver a plantear en términos de bivectores, dada una interpretación geométrica, y luego a menudo se resuelven más fácilmente o se relacionan geométricamente con otros problemas bivectoriales.^[24]

Más generalmente, cada álgebra geométrica real es isomórfica a un álgebra matricial. Esta última contiene a los bivectores como un subespacio, aunque a menudo de una manera que no es especialmente útil. Estas matrices son de interés principalmente como una forma de clasificar las álgebras de Clifford.^[25]

Véase también

• Multivector
• Álgebra multilineal

Referencias

1. Leo Dorst; Daniel Fontijne; Stephen Mann (2009). Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry (2nd edición). Morgan Kaufmann. p. 32. ISBN 978-0-12-374942-0. «El bivector algebraico no es específico en forma; geométricamente es una cantidad de área orientada en un plano específico, eso es todo.»
2. Lounesto (2001) p. 87
3. David Hestenes (1999). New foundations for classical mechanics: Fundamental Theories of Physics (2nd edición). Springer. p. 21. ISBN 978-0-7923-5302-7.
4. Lounesto (2001) p. 33
5. Karen Hunger Parshall; David E. Rowe (1997). The Emergence of the American Mathematical Research Community, 1876–1900. American Mathematical Society. p. 31 ff. ISBN 978-0-8218-0907-5.
6. Rida T. Farouki (2007). «Chapter 5: Quaternions». Pythagorean-hodograph curves: algebra and geometry inseparable. Springer. p. 60 ff. ISBN 978-3-540-73397-3.
7. A discussion of quaternions from these years is Alexander McAulay (1911). «Quaternions». The encyclopædia britannica: a dictionary of arts, sciences, literature and general information. Vol. 22 (11th edición). Cambridge University Press. p. 718 et seq.
8. Josiah Willard Gibbs; Edwin Bidwell Wilson (1901). Vector analysis: a text-book for the use of students of mathematics and physics. Yale University Press. p. 481 ff.
9. Philippe Boulanger; Michael A. Hayes (1993). Bivectors and waves in mechanics and optics. Springer. ISBN 978-0-412-46460-7.
10. PH Boulanger & M Hayes (1991). «Bivectors and inhomogeneous plane waves in anisotropic elastic bodies». En Julian J. Wu; Thomas Chi-tsai Ting & David M. Barnett, eds. Modern theory of anisotropic elasticity and applications. Society for Industrial and Applied Mathematics (SIAM). p. 280 et seq. ISBN 978-0-89871-289-6.
11. David Hestenes (30 de septiembre de 1999). op. cit. p. 61. ISBN 978-0-7923-5302-7.
12. Lounesto (2001) p. 35
13. Lounesto (2001) p. 86
14. Hestenes, David; Ziegler, Renatus (1991). «Projective Geometry with Clifford Algebra». Acta Applicandae Mathematicae 23: 25-63. doi:10.1007/bf00046919. Archivado desde el original el 3 de marzo de 2016. Consultado el 15 de julio de 2019.
15. Lounesto (2001) p.29
16. William E Baylis (1994). Theoretical methods in the physical sciences: an introduction to problem solving using Maple V. Birkhäuser. p. 234, see footnote. ISBN 978-0-8176-3715-6. «Los términos vector axial y pseudovector son a menudo tratados como sinónimos, pero es bastante útil distinguir (... el pseudovector) de su dual (... el vector axial).»
17. En términos matemáticos estrictos, los vectores axiales son un espacio vectorial n-dimensional con la estructura de grupo habitual GL(n,R), pero con la representación no estándar A → A det(A)/|det(A)|.
18. Chris Doran; Anthony Lasenby (2003). Geometric algebra for physicists. Cambridge University Press. p. 56. ISBN 978-0-521-48022-2.
19. Lounesto (2001) pp. 37–39
20. WildLinAlg episode 4, Norman J Wildberger, Univ. of New South Wales, 2010, lecture via youtube
21. Lounesto (2001) pp. 89–90
22. Lounesto (2001) pp. 109–110
23. Lounesto (2001) p.222
24. Lounesto (2001) p. 193
25. Lounesto (2001) p. 217

Referencias generales

• Leo Dorst; Daniel Fontijne; Stephen Mann (2009). «§ 2.3.3 Visualizing bivectors». Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry (2nd edición). Morgan Kaufmann. p. 31 ff. ISBN 978-0-12-374942-0.
• Whitney, Hassler (1957). Geometric Integration Theory. Princeton: Princeton University Press. ISBN 978-0-486-44583-0.

• Lounesto, Pertti (2001). Clifford algebras and spinors. Cambridge: Cambridge University Press. ISBN 978-0-521-00551-7. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).

• Chris Doran & Anthony Lasenby (2003). «§ 1.6 The outer product». Geometric Algebra for Physicists. Cambridge: Cambridge University Press. p. 11 et seq. ISBN 978-0-521-71595-9.

• Datos: Q663908
• Multimedia: Bivectors / Q663908