Teorema maestro de Ramanujan

En matemáticas, el teorema maestro de Ramanujan, llamado así en honor a Srinivasa Ramanujan,^[1] es una técnica que proporciona una expresión analítica para la transformada de Mellin de una función analítica.

Página de un cuaderno de Ramanujan declarando su teorema maestro.

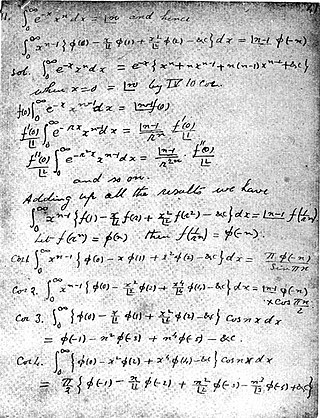
El resultado se muestra como sigue:

Si una función de variable compleja ${\textstyle f(x)}$ tiene una expresión de la forma

${\displaystyle f(x)=\sum _{k=0}^{\infty }{\frac {\,\varphi (k)\,}{k!}}(-x)^{k}}$

entonces la transformada de Mellin de ${\textstyle f(x)}$ está dada por

${\displaystyle \int _{0}^{\infty }x^{s-1}f(x)\,dx=\Gamma (s)\,\varphi (-s)}$

donde ${\textstyle \Gamma (s)}$ es la función gamma.

Esto fue usado ampliamente por Ramanujan para calcular integrales definidas y series infinitas.

Versiones en dimensiones altas de este teorema también aparecen en física cuántica (a través de diagramas de Feynman).^[2]

Un resultado similar fue también obtenido por Glaisher.^[3]

Formalismo alternativo

Una formulación alternativa del teorema maestro de Ramanujan es la siguiente:

${\displaystyle \int _{0}^{\infty }x^{s-1}\left(\,\lambda (0)-x\,\lambda (1)+x^{2}\,\lambda (2)-\,\cdots \,\right)dx={\frac {\pi }{\,\sin(\pi s)\,}}\,\lambda (-s)}$

la cual se convierte en la forma de arriba después de sustituir ${\textstyle \lambda (n)\equiv {\frac {\varphi (n)}{\,\Gamma (1+n)\,}}}$ y usando la ecuación funcional de la función gamma.

La integral de arriba es convergente para ${\textstyle 0<\operatorname {\mathcal {Re}} (s)<1}$ sujeta a las condiciones de crecimiento de ${\textstyle \varphi }$.^[4]

Demostración

Una demostración sujeta a supuestos "naturales" (aunque no a las condiciones necesarias más débiles) del teorema maestro de Ramanujan fue proporcionada por G. H. Hardy^[5] (capítulo XI) empleando el teorema de los residuos y el bien conocido teorema de inversión de Mellin.

Referencias

1. Berndt, B. (1985). Ramanujan's Notebooks, Part I. New York: Springer-Verlag.
2. González, Iván; Moll, V.H.; Schmidt, Iván (2011). «A generalized Ramanujan Master Theorem applied to the evaluation of Feynman diagrams». arXiv:1103.0588  [math-ph].
3. Glaisher, J.W.L. (1874). «A new formula in definite integrals». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 48 (315): 53-55. doi:10.1080/14786447408641072.
4. Amdeberhan, Tewodros; Gonzalez, Ivan; Harrison, Marshall; Moll, Victor H.; Straub, Armin (2012). «Ramanujan's Master Theorem». The Ramanujan Journal 29 (1–3): 103-120. S2CID 8886049. doi:10.1007/s11139-011-9333-y. Parámetro desconocido |citeseerx= ignorado (ayuda)
5. Hardy, G.H. (1978). Ramanujan: Twelve lectures on subjects suggested by his life and work (3rd edición). New York, NY: Chelsea. ISBN 978-0-8284-0136-4.

Enlaces externos

• «Ramanujan's Master Theorem». mathworld.wolfram.com.
• «rmt». ArminStraub. publications.

• Datos: Q7288993