Simetría cíclica en tres dimensiones

La simetría cíclica en tres dimensiones^[1] está integrada por cuatro series infinitas de grupos de puntos en tres dimensiones (n≥1) con simetría rotacional o reflexiva de multiplicidad n respecto a un eje (en un ángulo de 360°/n), tales que conservan la configuración de la situación de los puntos.

Grupos de puntos en tres dimensiones

Simetría involutiva Cs, (*) [ ] =	Simetría cíclica Cnv, (*nn) [n] =	Simetría diédrica Dnh, (*n22) [n,2] =
Grupo poliédrico, [n,3], (*n32)
Simetría tetraédrica Td, (*332) [3,3] =	Simetría octaédrica Oh, (*432) [4,3] =	Simetría icosaédrica Ih, (*532) [5,3] =

En geometría tridimensional se definen de acuerdo con los grupos de simetría finitos de un cono. Para n = ∞ corresponden a cuatro frisos. Se utiliza la notación de Schönflies. Los términos horizontal (h) y vertical (v) implican la existencia y dirección de reflexiones con respecto a un eje de simetría vertical. También se muestra la notación de Coxeter entre corchetes y la notación orbifold entre paréntesis.

Ejemplo de árbol de subgrupos de simetría para la simetría diédrica: D_4h, [4,2], (*224)

Tipos

Quiral

• C_n, [n]⁺, (nn) de orden n (es decir, con simetría n-rotacional), el grupo acro-n-gonal (grupo abstracto Z_n). Para n=1, sin simetría (el grupo trivial).

Aquirales

• C_nh, [n⁺,2], (n*) de orden 2n (es decir,simetría prismática o del grupo orto-n-gonal; el grupo abstracto Z_n × Dih₁); para n=1 esto se denota por C_s (1*) y se llama simetría especular, o también simetría bilateral. Tiene simetría especular con respecto a un plano perpendicular al eje de rotación n.

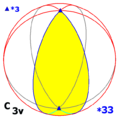
• C_nv, [n], (*nn) de orden 2n (simetría piramidal o del grupo completo acro-n-gonal; el grupo abstracto Dih_n); en biología C_2v se llama simetría birradial. Para n=1 se tiene nuevamente que C_s (1*). Tiene planos de simetría especular verticales. Este es el grupo de simetría de una pirámide regular de n lados.

• 'S_2n, [2⁺,2n⁺], (n×) de orden 2n (el grupo giro-n-gonal, que no debe confundirse con los grupos simétricos, para los cuales se usa la misma notación; es el grupo abstracto Z_2n). Tiene un eje de rotorreflexión de orden 2n, también llamado eje de rotación impropia de 2n, es decir, el grupo de simetría contiene una combinación de una reflexión en el plano horizontal y una rotación en un ángulo de 180°/n. Así, como D_nd, contiene un número de rotaciones impropias pero sin contener las rotaciones correspondientes.

• • Para n=1 se tiene que S₂ (1×), también denotado por C_i, también denominada simetría de inversión.

C_2h, [2,2⁺] (2*) y C_2v, [2], (*22) de orden 4 son dos de los tres tipos de grupos de simetría 3D con el grupo de Klein como grupo abstracto. C_2v se aplica, por ejemplo, para una loseta rectangular con su cara superior diferente de su cara inferior.

Grupos de frisos

Pieza de relleno de embalaje con simetría C_2h

En el límite, estos cuatro grupos representan los frisos en el plano euclídeo como C_∞, C_∞h, C_∞v y S_∞. Las rotaciones se convierten en traslaciones en el límite. Las porciones del plano infinito también se pueden cortar y conectar en un cilindro infinito.

Frisos

Notaciones				Ejemplos
IUC	Orbifold	Coxeter	Schönflies*	Plano euclídeo	Cilindro (n=6)
p1	∞∞	[∞]+	C∞
p1m1	*∞∞	[∞]	C∞v
p11m	∞*	[∞+,2]	C∞h
p11g	∞×	[∞+,2+]	S∞

Ejemplos

S2/Ci (1x):	C4v (*44):		C5v (*55):
Paralelepípedo	Pirámide cuadrada	Pirámide cuadrada elongada	Pirámide pentagonal

Véase también

• Simetría diédrica en tres dimensiones

Referencias

1. (Austria) Symposium on Graph Drawing 2001 (Vienna (2002). Graph Drawing: 9th International Symposium, GD 2001 Vienna, Austria, September 23-26, 2001, Revised Papers, Volumen 9. Springer Science & Business Media. pp. 190 de 524. ISBN 9783540433095. Consultado el 22 de agosto de 2022.

Bibliografía

• Sands, Donald E. (1993). «Crystal Systems and Geometry». Introduction to Crystallography. Mineola, New York: Dover Publications, Inc. p. 165. ISBN 0-486-67839-3.
• On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN 978-1-56881-134-5
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
• N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups

• Datos: Q5198233