Paralaje
diferencia en la posición aparente de un objeto visto a lo largo de dos líneas de visión diferentes De Wikipedia, la enciclopedia libre
El paralaje (del griego παράλλαξις [parálaksis], ‘cambio’, ‘diferencia’) es la desviación angular de la posición aparente de un objeto, dependiendo del punto de vista elegido.[1]
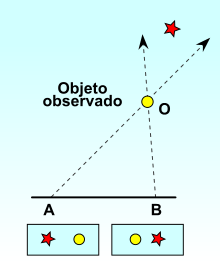
Al proyectar el objeto observado O contra un fondo suficientemente distante, la posición de O varía según el punto de vista en A o en B. Desde A, el objeto observado parece estar a la derecha de la lejana estrella roja, mientras que desde B se ve a la izquierda de aquella.
El ángulo AOB se denomina ángulo de paralaje, que abarca el segmento AB desde O.
Debido al acortamiento, los objetos cercanos muestran un paralaje mayor que los objetos lejanos, por lo que el paralaje puede utilizarse para determinar distancias.
Para medir grandes distancias, como la distancia de un planeta o una estrella a la Tierra, los astrónomos utilizan el principio de paralaje. En este caso, el término paralaje es el semiángulo de inclinación entre dos líneas de visión de la estrella, como se observa cuando la Tierra está en lados opuestos del Sol en su órbita.[2] Estas distancias forman el peldaño más bajo de lo que se denomina "la escalera de distancias cósmicas", el primero de una sucesión de métodos por los que los astrónomos determinan las distancias a los objetos celestes, sirviendo de base para otras mediciones de distancias en astronomía que forman los peldaños superiores de la escalera.
El paralaje también afecta a instrumentos ópticos como visores, binoculares, microscopios y cámara réflex de objetivos gemelos que ven objetos desde ángulos ligeramente diferentes. Muchos animales, junto con los humanos, tienen dos ojos con campos visuales superpuestos que utilizan el paralaje para obtener percepción de profundidad; este proceso se conoce como estereopsis. En visión por ordenador el efecto se utiliza para la visión estereoscópica por ordenador, y existe un dispositivo llamado telémetro de paralaje que lo utiliza para encontrar la distancia, y en algunas variaciones también la altitud a un objetivo.
Un sencillo ejemplo cotidiano de paralaje puede verse en los salpicaderos de los vehículos de motor que utilizan un velocímetro mecánico de aguja. Cuando se mira directamente desde delante, la velocidad puede ser exactamente 60, pero cuando se mira desde el asiento del pasajero, la aguja puede parecer que muestra una velocidad ligeramente diferente debido al ángulo de visión combinado con el desplazamiento de la aguja desde el plano de la esfera numérica.
Percepción visual
Resumir
Contexto

Dado que los ojos de los seres humanos y otros animales se encuentran en distintas posiciones en la cabeza, presentan distintas vistas simultáneamente. Esta es la base de la estereopsis, el proceso por el cual el cerebro explota el paralaje debido a las diferentes vistas del ojo para obtener la percepción de la profundidad y estimar las distancias a los objetos.[3]
Los animales también utilizan el paralaje de movimiento, en el que los animales (o sólo la cabeza) se mueven para obtener diferentes puntos de vista. Por ejemplo, las palomas (cuyos ojos no tienen campos de visión superpuestos y, por tanto, no pueden utilizar la estereopsis) mueven la cabeza arriba y abajo para ver la profundidad.[4] El paralaje de movimiento se explota también en el estereoscopia de meneo, gráficos por ordenador que proporcionan señales de profundidad a través de la animación de cambio de punto de vista en lugar de a través de la visión binocular.
Medición de la distancia
Resumir
Contexto
El paralaje surge debido a un cambio en el punto de vista que se produce por el movimiento del observador, del observado o de ambos. Lo esencial es el movimiento relativo. Al observar el paralaje, medir ángulos, y utilizando la geometría, se puede determinar la distancia.
La medición de distancias por paralaje es un caso especial del principio de triangulación, que afirma que se pueden resolver todos los lados y ángulos de una red de triángulos si, además de todos los ángulos de la red, se ha medido la longitud de al menos un lado. Así, la medición cuidadosa de la longitud de una línea de base puede fijar la escala de toda una red de triangulación. En la paralaje, el triángulo es extremadamente largo y estrecho, y midiendo tanto su lado más corto (el movimiento del observador) como el pequeño ángulo superior (siempre inferior a 1 arcosegundo,[5] dejando los otros dos cerca de 90 grados), se puede determinar la longitud de los lados largos (en la práctica considerados iguales).
En astronomía, suponiendo que el ángulo sea pequeño, la distancia a una estrella (medida en parsecs) es la recíproca del paralaje (medida en arco segundos): Por ejemplo, la distancia a Próxima Centauri es 1/0,7687 = 1.3009 parsecs (4,243 años luz).[6]

En la Tierra, se puede utilizar un telémetro de coincidencia o telémetro de paralaje para hallar la distancia a un objetivo. En topografía, el problema de resección explora las medidas angulares desde una línea de base conocida para determinar las coordenadas de un punto desconocido.
En astronomía
Resumir
Contexto
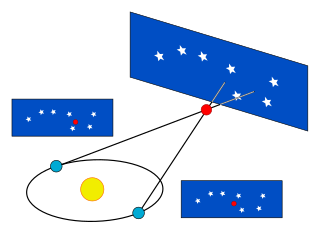

Las medidas de distancia fundamentales más importantes en astronomía proceden del paralaje trigonométrico, tal y como se aplica en el método del paralaje estelar. Cuando la Tierra orbita alrededor del Sol, la posición de las estrellas cercanas parece desplazarse ligeramente respecto al fondo más lejano. Estos desplazamientos son ángulos en un triángulo isósceles, con 2 AU (la distancia entre las posiciones extremas de la órbita de la Tierra alrededor del Sol) como base del triángulo y la distancia a la estrella como los catetos largos de igual longitud. La cantidad de desplazamiento es bastante pequeña, incluso para las estrellas más cercanas, midiendo 1 segundo de arco para un objeto a 1 parsec de distancia (3,26 año luzs), y a partir de entonces disminuyendo en cantidad angular a medida que aumenta la distancia. Los astrónomos suelen expresar las distancias en unidades de parsecs (arcosegundos de paralaje); en los medios populares se utilizan los años luz.
Dado que el paralaje se hace menor a mayor distancia estelar, sólo pueden medirse distancias útiles para estrellas que estén lo suficientemente cerca como para tener un paralaje mayor que unas pocas veces la precisión de la medición. En la década de 1990, por ejemplo, la misión Hipparcos obtuvo paralajes para más de cien mil estrellas con una precisión de aproximadamente un miliarcosegundo,[7] proporcionando distancias útiles para las estrellas hasta unos cientos de parsecs. La Wide Field Camera 3 del Hubble Space Telescope tiene el potencial de proporcionar una precisión de 20 a 40 micro segundos de arco, permitiendo mediciones de distancia fiables de hasta 5000 parsecs (16 000 ly) para un pequeño número de estrellas.[8][9] La misión espacial Gaia proporcionó distancias igualmente precisas a la mayoría de las estrellas más brillantes que la 15.ª magnitud.[10] Las distancias pueden medirse con una precisión del 10 % hasta el Centro Galáctico, a unos 30 000 años luz de distancia.
Las estrellas tienen una velocidad relativa al Sol que causa el movimiento propio (transversal a través del cielo) y la velocidad radial (movimiento hacia o desde el Sol). El primero se determina trazando la posición cambiante de las estrellas a lo largo de muchos años, mientras que la segunda procede de la medición del desplazamiento Doppler del espectro de la estrella causado por el movimiento a lo largo de la línea de visión. Para un grupo de estrellas con la misma clase espectral y un rango de magnitud similar, se puede obtener un paralaje medio a partir del análisis estadístico de los movimientos propios relativos a sus velocidades radiales. Este método de paralaje estadístico es útil para medir las distancias de estrellas brillantes más allá de 50 parsecs y estrellas variabless gigantes, incluyendo Cefeidas y las variables RR Lyrae.[11]
En astronomía se definen diversos tipos de paralaje. Estos son algunos:[12]
- El paralaje es el ángulo formado por la dirección de dos líneas visuales relativas a la observación de un mismo objeto desde dos puntos distintos, suficientemente alejados entre sí y no alineados con él. También suele emplearse este término para referirse a la distancia a las estrellas.

Paralaje anual
El paralaje anual es el máximo valor aparente que puede adquirir la posición de una estrella dada en el transcurso de un año debido a la posición variable de la Tierra en su órbita alrededor del Sol y que corresponderá al momento en que la longitud eclíptica de la estrella, que es siempre constante, difiera 90° de la longitud eclíptica de la Tierra, que varía constantemente.

En el año 1838, Friedrich Bessel fue el primero en determinar el paralaje de una estrella, 61 Cygni, en la constelación del Cisne. Dos años después, en 1840, Friedrich Georg Wilhelm von Struve logró medir el paralaje de Vega en la constelación de Lyra.
Los paralajes estelares están por debajo del segundo de arco. El sistema estelar más cercano a la Tierra es Alfa Centauri, un sistema formado por tres estrellas. La más cercana de ellas, Próxima Centauri, tiene un paralaje de 0,765", correspondiente a 1,31 pc, o 4,3 años luz.
A mayor distancia el paralaje es menor, y los errores cometidos se van haciendo más y más significativos, de modo que a partir de los 100 años luz ya no es fiable el paralaje anual trigonométrico para determinar distancias estelares.
Paralaje geocéntrico o paralaje diurno
El paralaje geocéntrico o paralaje diurno es la diferencia entre la dirección de un astro, visto desde un punto de la superficie de la Tierra (topocéntrico) y la misma dirección de ese astro visto desde el centro de la Tierra (geocéntrico).

Paralaje horizontal
El paralaje horizontal es el ángulo bajo el cual se vería el radio de la Tierra desde un astro cuando este se encuentra en el horizonte. Si el observador se sitúa en el ecuador, entonces, este paralaje recibe el nombre especial de «paralaje horizontal ecuatorial». El valor es máximo en el ecuador de la Tierra y varía con la latitud, al no ser la Tierra completamente esférica.
Paralaje trigonométrico
El paralaje trigonométrico es el ángulo bajo el cual se ve el radio de la órbita de la Tierra, desde una estrella a una distancia normalizada de una unidad astronómica. Se expresa en segundos de arco. La distancia a la estrella es el inverso del paralaje trigonométrico expresado en parsec; es decir que cuando se dice que el paralaje de Antares es de 0,019", significa que Antares se encuentra a 52,632 pársecs o 171,66 años luz.
Paralaje solar
El paralaje solar es el ángulo bajo el que se ve el radio ecuatorial de la Tierra desde el centro del Sol. Vale 8,794148".
Paralaje lunar
El paralaje lunar es el ángulo bajo el que se ve el radio ecuatorial de la Tierra desde el centro de la Luna. Vale 57'2,608".
Metrología
Resumir
Contexto

Las mediciones realizadas viendo la posición de algún marcador en relación con algo a medir están sujetas a error de paralaje si el marcador está a cierta distancia del objeto de medición y no se ve desde la posición correcta. Por ejemplo, si se mide la distancia entre dos marcas en una línea con una regla marcada en su superficie superior, el grosor de la regla separará sus marcas de las marcas. Si se mira desde una posición no exactamente perpendicular a la regla, la posición aparente se desplazará y la lectura será menos precisa de lo que la regla es capaz.
Un error similar ocurre cuando se lee la posición de un puntero contra una escala en un instrumento como un multímetro analógico. Para ayudar al usuario a evitar este problema, la escala se imprime a veces sobre una estrecha franja de espejo, y el ojo del usuario se coloca de modo que el puntero oculte su reflejo, garantizando que la línea de visión del usuario sea perpendicular al espejo y, por tanto, a la escala. El mismo efecto altera la velocidad leída en el velocímetro de un coche por un conductor situado delante y un pasajero situado a un lado, los valores leídos en un gratícula, no en contacto real con la pantalla de un osciloscopio, etc.
En fotografía
Resumir
Contexto
En fotografía el paralaje determina que lo captado por el fotógrafo a través del visor no coincide con la imagen capturada a través del objetivo de la cámara. Este desplazamiento por paralaje puede ser vertical, horizontal o ambos a la vez.

En este sentido, el «error de paralaje» se produce cuando se utiliza un visor que no está montado en el mismo eje que el objetivo. Es decir, el visor no previsualiza la propia imagen que le ofrece el objetivo.
En estos casos, cuando el visor está desplazado con respecto al objetivo la imagen que ofrece el visor no es exactamente la misma que luego se plasmará en la película (la que capta el objetivo), sino que estará mínimamente desplazada bien en su eje horizontal, bien en su eje vertical, o en ambos.
El error de paralaje se da en las cámaras compactas antiguas, en las que existe un visor independiente del objetivo para encuadrar la imagen antes de realizar la foto. En una cámara réflex de un solo objetivo no hay error de paralaje, ya que el fotógrafo observa la imagen a través del objetivo, reflejada por el espejo hacia el pentaprisma y el visor.
Este tipo de error también afecta al ojo humano; si no está a la altura del objeto observado, se pueden percibir falsas imágenes. En los laboratorios, hay que tener en cuenta este error, pues al llenar probetas u otros envases aforados, si no se observan desde la altura correcta, se aprecian mal las cantidades de materia, con los consecuentes errores en los cálculos.
El paralaje es mayor cuanto más cerca se encuentra el motivo que se va a fotografiar, mientras que a partir de varios metros el efecto se hace insignificante. Por esta razón, al encuadrar la imagen de una foto de algo que se encuentra cerca, debe tenerse en cuenta el paralaje, a fin de evitar que una parte de la imagen quede cortada en la fotografía. La mejor precaución consiste en encuadrar la fotografía con un margen adicional en todos los lados.
Espejo de paralaje
En dispositivos de medición analógicos (que usaban una aguja o manecilla) se colocaba un espejo de paralaje en forma de segmento de corona circular intercalado en el cuadrante de valores. Para la correcta lectura la aguja debía ocultar su propio reflejo (la observación se efectuaba cerrando un ojo).
Véase también
Referencias
Enlaces externos
Wikiwand - on
Seamless Wikipedia browsing. On steroids.

