En geometría, el gran dodecaedro es un poliedro de Kepler-Poinsot, con símbolo de Schläfli {5,5/2} y con diagrama de Coxeter-Dynkin de: 
.
| Gran dodecaedro | ||
|---|---|---|
| Familia: Sólido de Kepler-Poinsot | ||
 Imagen del sólido | ||
| Caras | 12 | |
| Aristas | 30 | |
| Vértices | 12 | |
| Grupo de simetría | Icosaédrico (Ih) | |
| Poliedro dual | Pequeño dodecaedro estrellado | |
Es uno de los cuatro poliedros regulares no convexos. Está compuesto de 12 caras pentagonales (seis pares de pentágonos paralelos), con cinco pentágonos que coinciden en cada vértice, que al cruzarse con cada uno de los otros genera un recorrido pentagrámico.
(Véase: Sólido de Kepler-Poinsot)
Imágenes
| Modelo transparente | Teselado Esférico |
|---|---|
 |
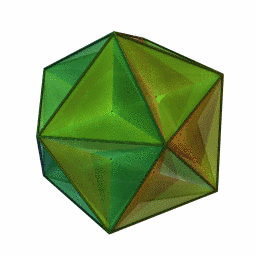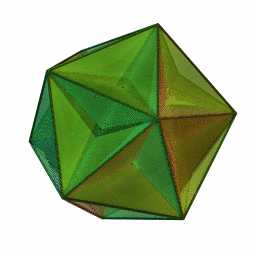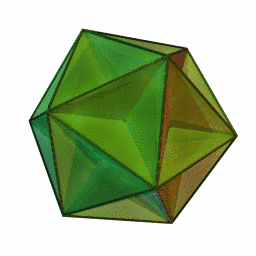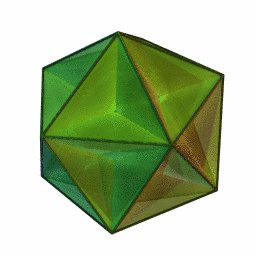Este poliedro representa un teselado esférico con una densidad de 3.
|
| Desarrollo del poliedro | Estelación |
20 x 
|
También puede ser construido como la segunda de tres estelaciones del dodecaedro, y referenciado como el modelo de Wenninger [W21]. |
Forma conjugada
La figura muestra el compuesto de pequeño dodecaedro estrellado y de gran dodecaedro, un poliedro compuesto donde el gran dodecaedro está situado en el interior de su poliedro dual, el pequeño dodecaedro estrellado.
Poliedros relacionados
Comparte la misma disposición de bordes con el icosaedro regular convexo.
Si se considera el gran dodecaedro como una superficie de intersección propiamente dicha, entonces tiene la misma topología que el triaquisicosaedro con pirámides cóncavas en vez de convexas.
Un proceso de truncado aplicado al gran dodecaedro produce una serie de poliedros uniformes no convexos. Este proceso se inicia con el gran dodecaedro truncado. Truncando los bordes por debajo de los vértices se produce el dodecadodecaedro como un gran dodecaedro rectificado. El proceso completado como una doble rectificación, reduciendo las caras originales a vértices produce el pequeño dodecaedro estrellado.
| Nombre | Pequeño dodecaedro estrellado | Dodecadodecaedro | Gran dodecaedro truncado | Gran dodecaedro |
|---|---|---|---|---|
| Diagrama de Coxeter-Dynkin |
|
|
|
|
| Figura |  |
 |
 |
|
Uso
- Esta forma es la base de la "Estrella de Alexander", rompecabezas similar al cubo de Rubik.
Véase también
Enlaces externos
- Eric W. Weisstein, Great dodecahedron (Uniform polyhedron) at MathWorld
- Weisstein, Eric W. «Three dodecahedron stellations». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Uniform polyhedra and duals
- Metal sculpture of Great Dodecahedron
Datos: Q1549165
Multimedia: Great dodecahedron / Q1549165
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
