Loading AI tools
población de asteroides que comparten elementos orbitales similares De Wikipedia, la enciclopedia libre
Una familia de asteroides es una población de asteroides con un origen común que comparten elementos orbitales similares como el semieje mayor, la excentricidad o la inclinación de la órbita.
Se cree que los miembros de las familias son fragmentos de colisiones de asteroides. La expresión familia de asteroides hace referencia a un concepto más específico que grupo de asteroides cuyos miembros, aun compartiendo algunas características orbitales, no tienen porqué tener un origen común.

Las grandes familias predominantes contienen varios centenares de asteroides reconocidos (y muchos más objetos aún más pequeños que puede ser que no se hayan analizado o incluso no descubiertos). Las familias pequeñas pueden tener del orden de unos diez miembros identificados. Se estima que alrededor del 33 % al 35 % de los objetos del cinturón de asteroides son miembros de alguna familia.
Se estima que existen alrededor de 20 a 30 familias reconocidas oficialmente o de manera fiable, así como varias decenas de grupos no definidos. La mayoría de las familias de asteroides se encuentran en el cinturón principal de asteroides, aunque varios grupos familiares como la familias de Palas, Focea o grupo de Hungaria se encuentran en un semieje mayor más pequeño o con una inclinación orbital superior al plano del cinturón principal.
Se ha identificado una familia asociada con el planeta enano Haumea.[1] Algunos estudios han tratado de encontrar evidencia de familias entre los asteroides troyanos, pero en la actualidad la evidencia no es concluyente.
En 1918, el astrónomo japonés Kiyotsugu Hirayama fue el primero en identificar familias de asteroides al plantear, analizando los elementos orbitales propios, que la similitud entre sí de las órbitas de algunos asteroides no podía deberse a la casualidad y postuló un origen común para dichos asteroides. Estableció que los miembros de una familia son los fragmentos resultantes de una colisión catastrófica.[2] En su honor, las familias que identificó son habitualmente conocidas como familias de Hirayama,[3] aunque a menudo se reserva este nombre para las cinco familias descubiertas por él.
En 1951, Dirk Brouwer reanudó los estudios de Hirayama, confirmando las familias identificadas por este y añadiendo otras nuevas.[4] Hasta 1990, diversos estudiosos propusieron sus propios catálogos de familias, basados en análisis propios y usando bases de datos diferentes, que elevaron el número de familias, pero condujeron a resultados discrepantes. Además, existió cierto grado de subjetividad en las investigaciones.[3] James R. Arnold, en 1969, suponía que los asteroides se dispersan siguiendo una distribución de Poisson.[5] B. E. Lindblad y R. B. Southworth, en 1971, calibraron su método para que se ajustara a los resultados de Brouwer,[6] mientras A. Carusi y E. Massaro, en 1978, hicieron lo propio para encontrar las familias clásicas de Hirayama.[7] J. G. Williams, en 1979, se basó en la inspección visual y una prueba estadística a posteriori.[8] Kozai, en 1979, reconoce un alto grado de arbitrariedad en su técnica. Todo esto, unido a la discrepancia en los resultados, plantearon dudas de la fiabilidad de las nuevas familias, por lo que solo las familias originales de Hirayama se tomaron en consideración para los estudios físicos.[3] Investigaciones posteriores en 1989 señalaron inconsistencias químicas en varias de las nuevas familias incompatibles con un origen común.[3]

Se cree que las familias se forman como resultado de colisiones entre asteroides. En muchos o la mayoría de los casos, el cuerpo progenitor se despedazó tras la colisión, pero también hay varias familias que resultaron de los escombros expulsados tras la formación de un cráter de impacto en el cuerpo principal (por ejemplo, las familias Vesta, Palas, Higía y Masalia). Dichas familias están constituidas por un cuerpo grande y un enjambre de pequeños asteroides. Algunas familias (por ejemplo, la familia Flora) poseen estructuras internas complejas que solo se podrían explicar si se hubieran sucedido varias colisiones en el mismo punto pero en diferentes momentos.
Debido a este proceso de formación, los miembros de las familias tienen composiciones muy similares en la mayoría de las familias. Aunque existen excepciones (como la familia Vesta) que se formó a partir de un gran cuerpo diferenciado.
Se cree que las familias de asteroides tiene una vida media del orden de mil millones de años, dependiendo de varios factores (por ejemplo, los asteroides más pequeños se pierden más rápido). Esto es significativamente un tiempo más corto que la edad del Sistema Solar, por lo que muy pocas son reliquias de la nebulosa protosolar. La progresiva desaparición de las familias ocurre tanto por la dispersión de las órbitas debido a las perturbaciones de Júpiter u otros cuerpos mayores, como por las colisiones entre los asteroides que los trituran resultando cuerpos más pequeños. Estos pequeños asteroides quedan sujetos a perturbaciones como el efecto Yarkovsky que puede empujarlos hacia resonancias gravitarorias con Júpiter con el tiempo. Una vez allí, son expulsados relativamente rápido del cinturón de asteroides. A su vez, los asteroides más grandes se van reduciendo por ulteriores colisiones. Se han obtenido estimaciones de edad para algunas familias, que van desde cientos de millones de años a menos de varios millones de años como es el caso de la familia de Karin. Se estima que las familias antiguas contienen pocos miembros pequeños, siendo esta es la base de determinación de su edad.
Se supone que algunas de las familias más antiguas han perdido a todos los miembros más pequeños y medianos, quedando solo una minoría de los más grandes, intactos. Un ejemplo sugerido de tales restos familiares antiguos son (9) Metis y (113) Amaltea. Otra evidencia de un gran número de antiguas familias (ahora dispersas o desaparecidas) proviene del análisis de la proporción de componentes químicos en meteoritos ferrosos. Estos muestran que en algún momento existieron entre 50 a 100 cuerpos progenitores lo suficientemente grandes como para diferenciarse, que tras sucesivos impactos llegaron a desintegrarse y así sus núcleos quedaron expuestos, resultando los meteoritos actuales.
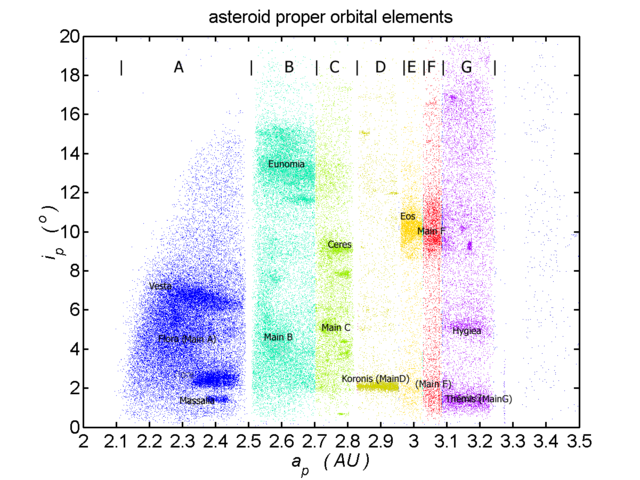
Cuando se trazan los elementos orbitales de los asteroides del cinturón principal (normalmente inclinación de la órbita frente a excentricidad o frente a semieje mayor), se observan algunas concentraciones distintas con relación a la distribución bastante uniforme del resto de asteroides en general. Estas concentraciones son las familias de asteroides.
Los intrusos son asteroides clasificados como miembros de la familia en función de sus llamados elementos orbitales, lo que sugiere que, al contrario de los verdaderos miembros de la familia, no se originaron en el mismo cuerpo parental que sufrió la colisión y fue fragmentado.

Estrictamente hablando, las familias y sus miembros se identifican por el análisis de los denominados elementos orbitales propios en vez de los actuales elementos orbitales que fluctúan en escalas de tiempo de decenas de miles de años. Los elementos propios son valores que permanecen constantes durante decenas de millones de años, y quizás más.
El empleo de técnicas asistidas por ordenador han permitido la identificación de más de cien familias. Los algorítmos más destacados en la búsqueda de nuevas familias son el método de agrupamiento jerárquico (HCM - Hierarchical Clustering Method), que busca agrupaciones a través de pequeñas distancias a los vecinos más próximos en el espacio de los elementos orbitales, y el método del análisis wavelet (WAM - Wavelet Analysis Method), que construye un mapa de densidad de los asteroides en el espacio del elemento orbital y busca picos de densidad.
Los límites de las familias son un tanto vagos porque en los bordes de las representaciones gráficas se funden con la densidad de fondo de los asteroides. Por este motivo, el número de miembros es incierto incluso entre los asteroides descubiertos, generalmente solo se conoce aproximadamente, y más para los que se encuentran en los límites de la familia.
Además, cabe la posibilidad de encontrar intrusos incluso en las regiones centrales de una familia bien delimitada. Puesto que se espera que los auténticos miembros de una familia tengan composiciones similares, la mayoría de intrusos se podrán reconocer en principio porque sus propiedades espectrales no coincidirán con las de la mayoría de los miembros de la familia. Un ejemplo notable es (1) Ceres que es intruso en la familia de Gefion que antaño llevó su nombre.
Las características espectrales también se utilizan para determinar la pertenencia o no de los asteroides de las zonas limítrofes de una familia, como se ha usado en el caso de la familia de Vesta cuyos miembros tienen una composición particular.
Los especialistas llaman a las familias de asteroides de diversas formas según su origen o constitución.
Como se mencionó anteriormente, las familias creadas a causa de un impacto que no desintegró el cuerpo del padre, sino que solo son los fragmentos expulsados del cráter, se denominan familias de cráteres. Se ha utilizado otra terminología para distinguir varios tipos de grupos que son menos distintos o menos estadísticamente ciertos de las "familias nominales" (o grupos) más prominentes.
Aquellas familias que se formaron con los restos de un impacto meteorítico se llaman cratering families.
El término grupo (cluster) se usa para describir a una familia pequeña o con pocos miembros conocidos, por ejemplo, el grupo de Karin.[9] También son conocidos como otro tipo de grupos (clumps) las familias con pocos miembros, pero claramente distintos del fondo, por ejemplo la familia de Juno. Los clanes (clans) son agrupaciones que destacan muy poco del fondo y/o tienen una estructura compleja que no permite decidir si son varias familias superpuestas o un solo grupo complejo, por ejemplo la familia de Flora. Las tribus (tribus) representan a los grupos menos seguros porque no destacan sobre la densidad de fondo o porque hay incertidumbre en los parámetros orbitales de los miembros.
| Distribución de las familias más destacadas, otras familias y resto de asteroides (hasta el número 398.000)[10] |
|---|
|
Nysa: 19,073 (4.8%) Vesta: 15,252 (3.8%) Flora: 13,786 (3.5%) Eos: 9,789 (2.5%) Coronis: 5,949 (1.5%) Eunomia: 5,670 (1.4%) Higía: 4,854 (1.2%) Temis: 4,782 (1.2%) Hungaria: 2,965 (0.7%) Resto de familias: 21,500 (5.4%) Resto de asteroides: 295,000 (74.0%) |
Entre las familias de asteroides, las familias de: Eos, Eunomia, Flora, Hungaria, Higía, Coronis, Nysa, Temis y Vesta son las que más destacan en el cinturón de asteroides.
En un estudio realizado en 2015, los investigadores concluyeron que se habían identificado 122 familias con un total de, aproximadamente, 100 000 miembros, basado en todo el catálogo de planetas menores numerados, que contaba con casi 400 000 asteroides numerados en ese momento (véase el índice del catálogo para obtener una lista actual de planetas menores numerados).[10] Los datos están accesibles en el "Small Bodies Data Ferret".[11] La primera columna de esta tabla contiene el número de identificación familiar (FIN - Family Identifier Number), que es un modo de etiquetar numéricamente a las familias identificadas, independientemente del nombre utilizado actualmente, ya que el nombre de una familia puede cambiar con observaciones refinadas, lo que lleva múltiples nombres utilizados en la literatura y para posterior confusión.[10]
| FIN | Familia | Lbl | # de Miembros | Huecos de Kirkwood | Taxonomía | media- albedo | Cuerpo principal·Resumen | Categoría | |
|---|---|---|---|---|---|---|---|---|---|
| 001 | Grupo de Hilda | HIL | 409 | rim | C | 0.04 | (153) Hilda; adj. Hildian; encabeza el grupo con el mismo nombre. (a–e–i: 3.7–4.2 AU; > 0.07; < 20°) | cat | |
| 002 | Familia de Schubart | SHU | 352 | rim | C | 0.03 | (1911) Schubart (incluida en el Grupo de Hilda) | cat | |
| 003 | Grupo de Hungaria | H | 2965 | rim | E | 0.35 | (434) Hungaria; ubicado dentro del grupo del mismo nombre. (a–e–i: 1.78–2.0 AU; < 0.18; 16°–34°) | cat | |
| 004 | Familia de Hektor | HEK | 12 | rim | – | – | (624) Hektor (troyano de Júpiter) | cat | |
| 005 | Familia de Eurybates | ERY | 218 | rim | CP | 0.06 | (3548) Eurybates (troyano de Júpiter) | cat | |
| 006 | unnamed family | 006 | 7 | rim | – | 0.06 | (9799) 1996 RJ (troyano de Júpiter) | — | |
| 007 | James Bond family[12] | 007 | 1 | inner | ASP | – | (9007) James Bond | — | |
| 008 | Familia de Arkesilaos | ARK | 37 | rim | – | – | (20961) Arkesilaos (troyano de Júpiter) | cat | |
| 009 | Familia de Ennomos | ENM | 30 | rim | – | 0.06 | (4709) Ennomos (troyano de Júpiter) | cat | |
| 010 | unnamed family | 010 | 13 | rim | – | 0.09 | (247341) 2001 UV209 (troyano de Júpiter) | — | |
| 401 | Familia de Vesta | V | 15252 | inner | V | 0.35 | (4) Vesta (adj. Vestian) | cat | |
| 402 | Familia de Flora (Ariadne family) | FLO | 13786 | inner | S | 0.30 | (8) Flora (adj. Florian), también denominada como (43) Ariadne; es lo que se conoce como clan de asteroides. No es una familia de asteroides legítima según Carruba y Milani, en cambio, la región central de Flora está etiquetada como familia de Belgica y familia de Duponta, respectivamente.[13][14] También engloba a los componentes de la anterior familia de Matterania. | cat | |
| 403 | Familia de Baptistina | BAP | 2500 | inner | X | 0.16 | (298) Baptistina, se fusiona con la Familia de Bélgica a 100 m/s según Carruba[14] | cat | |
| 404 | Familia de Massalia | MAS | 6424 | inner | S | 0.22 | (20) Massalia, adj. Massalian, a-e-i: (2.37 to 2.45; 0.12 to 0.21; 0.4 to 2.4) | cat | |
| 405 | Familia de Nysa (Familia de Herta; Familia de Eulalia) | NYS | 19073 | inner | SFC | 0.28 0.06 | (44) Nysa/(142) Polana también conocida como Familia de Herta ((135) Hertha). Incluye la Familia de Eulalia (495 Eulalia) | cat | |
| 406 | Familia de Erigone | ERI | 1776 | inner | CX | 0.06 | (163) Erigone, adj. Erigonian | cat | |
| 407 | Familia de Clarissa | CLA | 179 | inner | X | 0.05 | (302) Clarissa | cat | |
| 408 | Familia de Sulamitis | SUL | 303 | inner | C | 0.04 | (752) Sulamitis | cat | |
| 409 | Familia de Lucienne | LCI | 142 | inner | S | 0.22 | (1892) Lucienne | cat | |
| 410 | Familia de Euterpe | EUT | 474 | inner | S | 0.26 | (27) Euterpe | cat | |
| 411 | Familia de Datura | DAT | 6 | inner | S | 0.21 | (1270) Datura | cat | |
| 412 | Familia de Lucascavin | LCA | 3 | inner | S | – | (21509) Lucascavin | cat | |
| 413 | Familia de Klio | KLI | 330 | inner | C | 0.07 | (84) Klio | cat | |
| 414 | Familia de Chimaera | CIM | 108 | inner | CX | 0.06 | (623) Chimaera | cat | |
| 415 | Familia de Chaldaea | CHL | 132 | inner | C | 0.07 | (313) Chaldaea; alt. named after (1715) Salli by Masiero | cat | |
| 416 | Familia de Svea | SVE | 48 | inner | CX | 0.06 | (329) Svea | cat | |
| 417 | unnamed family | 417 | 9 | inner | – | – | (108138) 2001 GB11 | — | |
| 701 | Familia de Focea | PHO | 1989 | inner | S | 0.22 | (25) Phocaea | cat | |
| 501 | Familia de Juno | JUN | 1684 | middle | S | 0.25 | (3) Juno (adj. Junonian) | cat | |
| 502 | Familia de Eunomia | EUN | 5670 | middle | S | 0.19 | (15) Eunomia | cat | |
| 504 | Familia de Némesis | NEM | 1302 | middle | C | 0.05 | (128) Nemesis (adj. Nemesian); also named after (58) Concordia (adj. Concordian) and (3827) Zdenekhorský. Formerly Liberatrix family by Zappalà (1995) and Cellino (2002) | cat | |
| 505 | Familia de Adeona | ADE | 2236 | middle | C | 0.07 | (145) Adeona | cat | |
| 506 | Familia de María | MAR | 2940 | middle | S | 0.25 | (170) Maria; alternatively named after 472 Roma.[15] | cat | |
| 507 | Familia de Padua | PAD | 1087 | middle | X | 0.10 | (363) Padua; also known as Lydia family(110) Lydia·adj. Paduan; Lydian | cat | |
| 508 | Familia de Aeolia | AEO | 296 | middle | X | 0.17 | (396) Aeolia | cat | |
| 509 | Familia de Chloris | CLO | 424 | middle | C | 0.06 | (410) Chloris, adj. Chloridian | cat | |
| 510 | Familia de Misa | MIS | 702 | middle | C | 0.03 | (569) Misa, adj. Misian | cat | |
| 511 | Familia de Brangäne | BRG | 195 | middle | S | 0.10 | (606) Brangäne | cat | |
| 512 | Familia de Dora | DOR | 1259 | middle | C | 0.05 | (668) Dora, adj. Dorian | cat | |
| 513 | Familia de Merxia | MRX | 1215 | middle | S | 0.23 | (808) Merxia, adj. Merxian | cat | |
| 514 | Familia de Agnia | AGN | 2125 | middle | S | 0.18 | (847) Agnia | cat | |
| 515 | Familia de Astrid | AST | 489 | middle | C | 0.08 | (1128) Astrid, adj. Astridian | cat | |
| 516 | Familia de Gefion (Ceres family; Minerva family) | GEF | 2547 | middle | S | 0.20 | (1272) Gefion, adj. Gefionian; a-e-i: (2.74 to 2.82; 0.08 to 0.18; 7.4 to 10.5); also known as Ceres family (adj. Cererian) after (1) Ceres; and Minerva (adj. Minervian) family after 93 Minerva (identified interloper) | cat | |
| 517 | Familia de König | KON | 354 | middle | CX | 0.04 | (3815) König | cat | |
| 518 | Familia de Rafita | RAF | 1295 | middle | S | 0.25 | (1644) Rafita, adj. Rafitian (namesake is a suspected interloper; not listed in family) | cat | |
| 519 | Familia de Hoffmeister | HOF | 1819 | middle | CF | 0.04 | (1726) Hoffmeister | cat | |
| 520 | Familia de Iannini | IAN | 150 | middle | S | 0.32 | (4652) Iannini | cat | |
| 521 | Familia de Kazuya | KAZ | 44 | middle | S | 0.21 | (7353) Kazuya | cat | |
| 522 | Familia de Ino | INO | 463 | middle | S | 0.24 | (173) Ino | cat | |
| 523 | Familia de Emilkowalski | EMI | 4 | middle | S | 0.20 | (14627) Emilkowalski | cat | |
| 524 | Familia de Brugmansia | 524 | 3 | middle | S | – | (16598) Brugmansia | cat | |
| 525 | Familia de Schulhof | SHF | 5 | middle | S | 0.27 | (2384) Schulhof | cat | |
| 526 | unnamed family | 526 | 58 | middle | C | 0.06 | (53546) 2000 BY6 | — | |
| 527 | Familia de Lorre | LOR | 2 | middle | C | 0.05 | (5438) Lorre | cat | |
| 528 | Familia de Leonidas | LEO | 135 | middle | CX | 0.07 | (2782) Leonidas; identical to the Vibilia family: VIB (and listed as such) | cat | |
| 529 | Familia de Vibilia | VIB | 180 | middle | C | 0.06 | (144) Vibilia; namesake only listed in family by Zappalà, but not by Nesvorý; identical to the Leonidas family: LEO. | cat | |
| 530 | Familia de Phaeo | PAE | 146 | middle | X | 0.06 | (322) Phaeo | cat | |
| 531 | Familia de Mitidika | MIT | 653 | middle | C | 0.06 | (2262) Mitidika (not listed in family itself) | cat | |
| 532 | Familia de Henan | HEN | 1872 | middle | L | 0.20 | (2085) Henan | cat | |
| 533 | Familia de Hanna | HNA | 280 | middle | CX | 0.05 | (1668) Hanna | cat | |
| 534 | Familia de Karma | KRM | 124 | middle | CX | 0.05 | (3811) Karma | cat | |
| 535 | Familia de Witt | WIT | 1618 | middle | S | 0.26 | (2732) Witt | cat | |
| 536 | Familia de Xizang | XIZ | 275 | middle | – | 0.12 | (2344) Xizang | cat | |
| 537 | Familia de Watsonia | WAT | 99 | middle | L | 0.13 | (729) Watsonia | cat | |
| 538 | Familia de Jones | JNS | 22 | middle | T | 0.05 | (3152) Jones | cat | |
| 539 | Familia de Aëria | AER | 272 | middle | X | 0.17 | (369) Aeria | cat | |
| 540 | Familia de Julia | JUL | 33 | middle | S | 0.19 | (89) Julia | cat | |
| 541 | Familia de Postrema | POS | 108 | middle | CX | 0.05 | (1484) Postrema | cat | |
| 801 | Familia de Palas | PAL | 128 | middle | B | 0.16 | (2) Pallas (adj. Palladian) | cat | |
| 802 | Familia de Gallia | GAL | 182 | middle | S | 0.17 | (148) Gallia | cat | |
| 803 | Familia de Hansa | HNS | 1094 | middle | S | 0.26 | (480) Hansa adj. Hansian; a-e-i: (~2.66; ~0.06; ~22.0°)[16] | cat | |
| 804 | Familia de Gersuind | GER | 415 | middle | S | 0.15 | (686) Gersuind | cat | |
| 805 | Familia de Barcelona | BAR | 306 | middle | S | 0.25 | (945) Barcelona | cat | |
| 806 | Familia de Tina | TIN | 96 | middle | X | 0.34 | (1222) Tina | cat | |
| 807 | Familia de Brucato | BRU | 342 | middle | CX | 0.06 | (4203) Brucato | cat | |
| 601 | Familia de Higía | HYG | 4854 | outer | CB | 0.06 | (10) Hygiea | cat | |
| 602 | Familia de Temis | THM | 4782 | outer | C | 0.07 | (24) Themis (adj. Themistian) | cat | |
| 603 | Familia de Sylvia | SYL | 255 | outer | X | 0.05 | (87) Sylvia; family within Cybele group | cat | |
| 604 | Familia de Meliboea | MEL | 444 | outer | C | 0.05 | (137) Meliboea, adj. Meliboean | cat | |
| 605 | Familia de Coronis | KOR | 5949 | outer | S | 0.15 | (158) Koronis, también conocida como familia de (208) Lacrimosa | cat | |
| 606 | Familia de Eos | EOS | 9789 | outer | K | 0.13 | (221) Eos | cat | |
| 607 | Familia de Emma | EMA | 76 | outer | C | 0.05 | (283) Emma | cat | |
| 608 | Familia de Brasilia | BRA | 579 | outer | X | 0.18 | (293) Brasilia, adj. Brazilian (namesake is a suspected interloper; not listed in family) | cat | |
| 609 | Familia de Veritas | VER | 1294 | outer | CPD | 0.07 | (490) Veritas, adj. Veritasian; alt: Undina (Undinian) family after 92 Undina | cat | |
| 610 | Familia de Karin | KAR | 541 | outer | S | 0.21 | (832) Karin. Recently formed family located within the Koronis family.[10]: 8, 18 | cat | |
| 611 | Familia de Naëma | NAE | 301 | outer | C | 0.08 | (845) Naëma, adj. Naëmian | cat | |
| 612 | Familia de Tirela | TIR | 1395 | outer | S | 0.07 | (1400) Tirela (Klumpkea) | cat | |
| 613 | Familia de Lixiaohua | LIX | 756 | outer | CX | 0.04 | (3556) Lixiaohua | cat | |
| 614 | Familia de Telramund | TEL | 468 | outer | S | 0.22 | (9506) Telramund; alternatively named after (179) Klytaemnestra by Masiero and by Milani | cat | |
| 615 | unnamed family | 615 | 104 | outer | CX | 0.17 | (18405) 1993 FY12 | — | |
| 616 | Familia de Charis | CHA | 808 | outer | C | 0.08 | (627) Charis | cat | |
| 617 | Familia de Theobalda | THB | 376 | outer | CX | 0.06 | (778) Theobalda, adj. Theobaldian; a-e-i: (3.16 to 3.19; 0.24 to 0.27; 14 to 15) | cat | |
| 618 | Familia de Terentia | TRE | 79 | outer | C | 0.07 | (1189) Terentia | cat | |
| 619 | Familia de Lau | LAU | 56 | outer | S | 0.27 | (10811) Lau | cat | |
| 620 | Familia de Beagle | BGL | 148 | outer | C | 0.09 | (656) Beagle. Recently formed family is located within the Themis family (all members are also listed as Themistians). Includes (7968) Elst–Pizarro.[10]: 7, 8, 18 | cat | |
| 621 | Familia de Koronis | K-2 | 246 | outer | S | 0.14 | (158) Koronis "second family" | cat | |
| 622 | Familia de Terpsichore | TRP | 138 | outer | C | 0.05 | (81) Terpsichore | cat | |
| 623 | Familia de Fringilla | FIR | 134 | outer | X | 0.05 | (709) Fringilla | cat | |
| 624 | Familia de Durisen | DUR | 27 | outer | X | 0.04 | (5567) Durisen | cat | |
| 625 | Familia de Yakovlev | YAK | 67 | outer | C | 0.05 | (5614) Yakovlev | cat | |
| 626 | Familia de San Marcello | SAN | 144 | outer | X | 0.19 | (7481) San Marcello | cat | |
| 627 | unnamed family | 627 | 38 | outer | CX | 0.05 | (15454) 1998 YB3 | — | |
| 628 | unnamed family | 628 | 248 | outer | S | 0.10 | (15477) 1999 CG1 | — | |
| 629 | unnamed family | 629 | 58 | outer | S | 0.21 | (36256) 1999 XT17 | — | |
| 630 | Familia de Aegle | AEG | 99 | outer | CX | 0.07 | (96) Aegle | cat | |
| 631 | Familia de Ursula | URS | 1466 | outer | CX | 0.06 | (375) Ursula | cat | |
| 632 | Familia de Elfriede | ELF | 63 | outer | C | 0.05 | (618) Elfriede | cat | |
| 633 | Familia de Itha | ITH | 54 | outer | S | 0.23 | (918) Itha | cat | |
| 634 | Familia de Inarradas | INA | 38 | outer | CX | 0.07 | (3438) Inarradas | cat | |
| 635 | Familia de Anfimov | ANF | 58 | outer | S | 0.16 | (7468) Anfimov | cat | |
| 636 | Familia de Marconia | MRC | 34 | outer | CX | 0.05 | (1332) Marconia | cat | |
| 637 | unnamed family | 637 | 64 | outer | CX | 0.05 | (106302) 2000 UJ87 | — | |
| 638 | Familia de Croatia | CRO | 93 | outer | X | 0.07 | (589) Croatia | cat | |
| 639 | Familia de Imhilde | IMH | 43 | outer | CX | 0.05 | (926) Imhilde | cat | |
| 640 | Familia de Gibbs | GBS | 8 | outer | – | – | 331P/Gibbs "P/2012 F5 (Gibbs)" | — | – |
| 641 | Familia de Juliana | JLI | 76 | outer | CX | 0.05 | (816) Juliana | cat | |
| 901 | Familia de Euphrosyne | EUP | 2035 | outer | C | 0.06 | (31) Euphrosyne | cat | |
| 902 | Familia de Alauda | ALA | 1294 | outer | B | 0.07 | (702) Alauda | cat | |
| 903 | Familia de Ulla | ULA | 26 | outer | X | 0.05 | (909) Ulla; family within Cybele group | cat | |
| 904 | Familia de Luthera | LUT | 163 | outer | X | 0.04 | (1303) Luthera; fam. is also named after 781 Kartvelia | cat | |
| 905 | Familia de Armenia | ARM | 40 | outer | C | 0.05 | (780) Armenia | cat |
En las siguientes tablas se muestran datos estadísticos de algunas familias de asteroides.[17]
| Familia asteroidal | Semieje mayor (ua) | Excentricidad | Inclinación (seno) | ||||
|---|---|---|---|---|---|---|---|
| Nombre | Miembros | Mínimo | Máximo | Mínima | Máxima | Mínimo | Máximo |
| (4) Vesta | 7865 | 2,256 | 2,482 | 0,080 | 0,127 | 0,100 | 0,132 |
| (5) Astraea | 2120 | 2,552 | 2,610 | 0,146 | 0,236 | 0,054 | 0,095 |
| (10) Hygiea | 2402 | 3,067 | 3,241 | 0,100 | 0,166 | 0,073 | 0,105 |
| (15) Eunomia | 6845 | 2,521 | 2,731 | 0,117 | 0,181 | 0,203 | 0,256 |
| (20) Massalia | 4758 | 2,335 | 2,474 | 0,145 | 0,175 | 0,019 | 0,033 |
| (24) Themis | 3950 | 3,062 | 3,240 | 0,114 | 0,192 | 0,009 | 0,048 |
| (93) Minerva | 1833 | 2,720 | 2,816 | 0,115 | 0,155 | 0,147 | 0,169 |
| (135) Hertha | 11 428 | 2,288 | 2,478 | 0,134 | 0,206 | 0,032 | 0,059 |
| (145) Adeona | 1399 | 2,573 | 2,714 | 0,153 | 0,181 | 0,193 | 0,213 |
| (158) Koronis | 5601 | 2,816 | 2,985 | 0,016 | 0,101 | 0,029 | 0,047 |
| (170) Maria | 2030 | 2,523 | 2,673 | 0,067 | 0,128 | 0,231 | 0,269 |
| (221) Eos | 10 336 | 2,950 | 3,146 | 0,022 | 0,133 | 0,148 | 0,212 |
| (434) Hungaria | 1117 | 1,883 | 1,988 | 0,051 | 0,097 | 0,344 | 0,378 |
| (490) Veritas | 1136 | 3,143 | 3,196 | 0,049 | 0,079 | 0,151 | 0,172 |
| (668) Dora | 1101 | 2,744 | 2,811 | 0,188 | 0,204 | 0,129 | 0,143 |
| (847) Agnia | 2033 | 2,713 | 2,819 | 0,063 | 0,083 | 0,056 | 0,076 |
| (1040) Klumpkea | 1096 | 3,083 | 3,174 | 0,176 | 0,217 | 0,279 | 0,298 |
| (1726) Hoffmeister | 1315 | 2,754 | 2,818 | 0,041 | 0,053 | 0,066 | 0,088 |
| (2076) Levin | 1145 | 2,254 | 2,323 | 0,130 | 0,153 | 0,088 | 0,106 |
| Familia asteroidal | Semieje mayor (ua) | Excentricidad | Inclinación (seno) | ||||
|---|---|---|---|---|---|---|---|
| Nombre | Miembros | Mínimo | Máximo | Mínima | Máxima | Mínimo | Máximo |
| (25) Phocaea | 944 | 2,261 | 2,415 | 0,160 | 0,265 | 0,366 | 0,425 |
| (31) Euphrosyne | 968 | 3,082 | 3,225 | 0,150 | 0,231 | 0,431 | 0,459 |
| (87) Sylvia | 139 | 3,459 | 3,564 | 0,046 | 0,073 | 0,162 | 0,179 |
| (110) Lydia | 729 | 2,696 | 2,779 | 0,026 | 0,061 | 0,084 | 0,106 |
| (163) Erigone | 392 | 2,332 | 2,374 | 0,200 | 0,218 | 0,081 | 0,098 |
| (173) Ino | 154 | 2,708 | 2,770 | 0,159 | 0,180 | 0,229 | 0,239 |
| (179) Klytaemnestra | 366 | 2,955 | 3,015 | 0,053 | 0,080 | 0,148 | 0,159 |
| (194) Prokne | 252 | 2,522 | 2,691 | 0,154 | 0,196 | 0,293 | 0,315 |
| (283) Emma | 369 | 3,029 | 3,084 | 0,107 | 0,124 | 0,155 | 0,166 |
| (293) Brasilia | 443 | 2,832 | 2,872 | 0,119 | 0,133 | 0,256 | 0,264 |
| (298) Baptistina | 131 | 2,261 | 2,288 | 0,146 | 0,161 | 0,100 | 0,114 |
| (302) Clarissa | 143 | 2,385 | 2,418 | 0,104 | 0,111 | 0,056 | 0,060 |
| (375) Ursula | 502 | 3,096 | 3,241 | 0,059 | 0,130 | 0,264 | 0,299 |
| (396) Aeolia | 242 | 2,731 | 2,750 | 0,164 | 0,170 | 0,057 | 0,062 |
| (480) Hansa | 839 | 2,538 | 2,721 | 0,008 | 0,101 | 0,364 | 0,385 |
| (507) Laodica | 149 | 3,124 | 3,207 | 0,049 | 0,075 | 0,181 | 0,198 |
| (569) Misa | 389 | 2,623 | 2,693 | 0,169 | 0,183 | 0,035 | 0,045 |
| (606) Brangäne | 153 | 2,573 | 2,594 | 0,179 | 0,183 | 0,166 | 0,168 |
| (752) Sulamitis | 158 | 2,421 | 2,484 | 0,084 | 0,095 | 0,085 | 0,092 |
| (778) Theobalda | 229 | 3,158 | 3,191 | 0,240 | 0,261 | 0,243 | 0,253 |
| (808) Merxia | 805 | 2,705 | 2,805 | 0,125 | 0,143 | 0,080 | 0,093 |
| (845) Naëma | 253 | 2,917 | 2,953 | 0,029 | 0,041 | 0,205 | 0,209 |
| (883) Matterania | 132 | 2,213 | 2,259 | 0,140 | 0,151 | 0,092 | 0,102 |
| (945) Barcelona | 219 | 2,599 | 2,659 | 0,190 | 0,289 | 0,506 | 0,521 |
| (1128) Astrid | 389 | 2,754 | 2,817 | 0,045 | 0,053 | 0,008 | 0,018 |
| (1298) Nocturna | 143 | 3,088 | 3,220 | 0,105 | 0,123 | 0,104 | 0,123 |
| (1303) Luthera | 179 | 3,193 | 3,236 | 0,106 | 0,144 | 0,310 | 0,337 |
| (1338) Duponta | 104 | 2,259 | 2,302 | 0,119 | 0,130 | 0,075 | 0,091 |
| (1547) Nele | 108 | 2,641 | 2,650 | 0,267 | 0,270 | 0,211 | 0,212 |
| (1658) Innes | 558 | 2,546 | 2,626 | 0,165 | 0,185 | 0,123 | 0,142 |
| (1911) Schubart | 280 | 3,964 | 3,967 | 0,159 | 0,222 | 0,041 | 0,055 |
| (3330) Gantrisch | 600 | 3,123 | 3,174 | 0,184 | 0,212 | 0,171 | 0,184 |
| (3815) König | 283 | 2,563 | 2,583 | 0,138 | 0,143 | 0,145 | 0,164 |
| (3827) Zdeněkhorský | 671 | 2,705 | 2,768 | 0,082 | 0,096 | 0,080 | 0,094 |
| (5026) Martes | 346 | 2,368 | 2,415 | 0,200 | 0,217 | 0,082 | 0,096 |
| (10955) Harig | 428 | 2,671 | 2,739 | 0,005 | 0,026 | 0,100 | 0,113 |
| (12739) 1992 DY7 | 240 | 2,682 | 2,746 | 0,047 | 0,060 | 0,031 | 0,041 |
| (13314) 1998 RH71 | 146 | 2,756 | 2,801 | 0,170 | 0,183 | 0,069 | 0,078 |
| (18466) Hakodate | 155 | 2,763 | 2,804 | 0,171 | 0,182 | 0,229 | 0,236 |
| (19466) Darcydiegel | 125 | 2,724 | 2,761 | 0,007 | 0,020 | 0,103 | 0,111 |
| Familia asteroidal | Semieje mayor (ua) | Excentricidad | Inclinación (seno) | ||||
|---|---|---|---|---|---|---|---|
| Nombre | Miembros | Mínimo | Máximo | Mínima | Máxima | Mínimo | Máximo |
| (2) Pallas | 38 | 2,756 | 2,791 | 0,254 | 0,283 | 0,531 | 0,550 |
| (63) Ausonia | 70 | 2,383 | 2,401 | 0,118 | 0,127 | 0,107 | 0,118 |
| (96) Aegle | 100 | 3,036 | 3,070 | 0,176 | 0,189 | 0,280 | 0,289 |
| (148) Gallia | 95 | 2,712 | 2,812 | 0,116 | 0,150 | 0,420 | 0,430 |
| (159) Aemilia | 45 | 3,091 | 3,131 | 0,111 | 0,117 | 0,084 | 0,090 |
| (410) Chloris | 93 | 2,713 | 2,761 | 0,238 | 0,265 | 0,146 | 0,160 |
| (618) Elfriede | 46 | 3,177 | 3,200 | 0,056 | 0,059 | 0,270 | 0,277 |
| (729) Watsonia | 75 | 2,720 | 2,814 | 0,110 | 0,144 | 0,294 | 0,305 |
| (780) Armenia | 41 | 3,085 | 3,129 | 0,060 | 0,074 | 0,310 | 0,314 |
| (1118) Hanskya | 77 | 3,145 | 3,246 | 0,035 | 0,059 | 0,252 | 0,266 |
| (1189) Terentia | 38 | 2,904 | 2,936 | 0,071 | 0,075 | 0,192 | 0,194 |
| (1222) Tina | 68 | 2,769 | 2,803 | 0,068 | 0,113 | 0,350 | 0,359 |
| (2782) Leonidas | 92 | 2,657 | 2,701 | 0,185 | 0,197 | 0,061 | 0,072 |
| (2967) Vladisvyat | 52 | 3,150 | 3,224 | 0,092 | 0,124 | 0,295 | 0,303 |
| (3110) Wagman | 86 | 2,554 | 2,592 | 0,134 | 0,145 | 0,049 | 0,065 |
| (3438) Inarradas | 34 | 3,036 | 3,067 | 0,176 | 0,186 | 0,249 | 0,255 |
| (3460) Ashkova | 52 | 3,159 | 3,218 | 0,187 | 0,209 | 0,016 | 0,028 |
| (3489) Lottie | 57 | 2,390 | 2,413 | 0,090 | 0,096 | 0,103 | 0,109 |
| (3811) Karma | 49 | 2,547 | 2,579 | 0,101 | 0,110 | 0,185 | 0,190 |
| (4945) Ikenozenni | 71 | 2,570 | 2,596 | 0,235 | 0,244 | 0,087 | 0,096 |
| (5651) Traversa | 42 | 3,097 | 3,166 | 0,112 | 0,128 | 0,231 | 0,241 |
| (6124) Mecklenburg | 57 | 3,966 | 3,967 | 0,186 | 0,212 | 0,146 | 0,159 |
| (6138) Hutton | 48 | 2,343 | 2,357 | 0,204 | 0,215 | 0,039 | 0,045 |
| (6769) Brokoff | 45 | 2,398 | 2,431 | 0,148 | 0,155 | 0,051 | 0,056 |
| (7220) Philnicholson | 49 | 2,418 | 2,424 | 0,183 | 0,195 | 0,026 | 0,036 |
| (7468) Anfimov | 45 | 3,031 | 3,075 | 0,087 | 0,091 | 0,060 | 0,061 |
| (7744) 1986 QA1 | 78 | 2,635 | 2,670 | 0,069 | 0,075 | 0,042 | 0,049 |
| (8737) Takehiro | 37 | 3,116 | 3,141 | 0,112 | 0,121 | 0,207 | 0,211 |
| (8905) Bankakuko | 49 | 2,599 | 2,620 | 0,181 | 0,190 | 0,084 | 0,091 |
| (11882) 1990 RA3 | 66 | 2,683 | 2,708 | 0,059 | 0,066 | 0,031 | 0,040 |
| (16286) 4057 P-L | 68 | 2,846 | 2,879 | 0,038 | 0,047 | 0,102 | 0,111 |
| (17392) 1981 EY40 | 75 | 2,645 | 2,679 | 0,059 | 0,070 | 0,036 | 0,042 |
| (18405) 1993 FY12 | 85 | 2,832 | 2,858 | 0,103 | 0,110 | 0,158 | 0,162 |
| (21344) 1997 EM | 62 | 2,709 | 2,741 | 0,150 | 0,159 | 0,046 | 0,050 |
| (21885) 1999 UY27 | 42 | 3,079 | 3,112 | 0,026 | 0,035 | 0,184 | 0,188 |
| (22241) 4072 T-3 | 40 | 3,082 | 3,096 | 0,126 | 0,133 | 0,087 | 0,096 |
| (25315) 1999 AZ8 | 53 | 2,575 | 2,596 | 0,243 | 0,251 | 0,090 | 0,096 |
| (28804) 2000 HC81 | 46 | 2,589 | 2,601 | 0,146 | 0,156 | 0,063 | 0,070 |
| (29841) 1999 FO14 | 53 | 2,639 | 2,668 | 0,052 | 0,059 | 0,033 | 0,040 |
| (31811) 1999 NA41 | 90 | 3,096 | 3,138 | 0,060 | 0,075 | 0,178 | 0,188 |
| (32418) 2000 RD33 | 48 | 2,763 | 2,795 | 0,255 | 0,261 | 0,152 | 0,156 |
| (43176) 1999 XM196 | 47 | 3,109 | 3,152 | 0,065 | 0,074 | 0,174 | 0,183 |
| (53546) 2000 BY6 | 47 | 2,709 | 2,735 | 0,170 | 0,174 | 0,247 | 0,251 |
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.