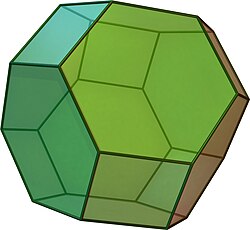
Truncated octahedron

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron G_IV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron.

Truncated octahedron
Type	Archimedean solid, Parallelohedron, Permutohedron, Plesiohedron, Zonohedron
Faces	14
Edges	36
Vertices	24
Symmetry group	octahedral symmetry ${\displaystyle \mathrm {O} _{\mathrm {h} }}$
Dual polyhedron	tetrakis hexahedron
Vertex figure
Net

The truncated octahedron was called the "mecon" by Buckminster Fuller.^[1]

Its dual polyhedron is the tetrakis hexahedron. If the original truncated octahedron has unit edge length, its dual tetrakis hexahedron has edge lengths ⁠9/8⁠√2 and ⁠3/2⁠√2.

Classifications

As an Archimedean solid

A truncated octahedron is constructed from a regular octahedron by cutting off all vertices. This resulting polyhedron has six squares and eight hexagons, leaving out six square pyramids. Setting the edge length of the regular octahedron equal to ${\displaystyle 3a}$, it follows that the length of each edge of a square pyramid (to be removed) is ${\displaystyle a}$ (the square pyramid has four equilateral triangles as faces, the first Johnson solid). From the equilateral square pyramid's property, its volume is ${\textstyle {\tfrac {\sqrt {2}}{6}}a^{3}}$. Because six equilateral square pyramids are removed by truncation, the volume of a truncated octahedron ${\displaystyle V}$ is obtained by subtracting the volume of those six from that of a regular octahedron:^[2] $${\displaystyle V={\frac {\sqrt {2}}{3}}(3a)^{3}-6\cdot {\frac {\sqrt {2}}{6}}a^{3}=8{\sqrt {2}}a^{3}\approx 11.3137a^{3}.}$$ The surface area of a truncated octahedron ${\displaystyle A}$ can be obtained by summing all polygonals' area, six squares and eight hexagons. Considering the edge length ${\displaystyle a}$, this is:^[2] $${\displaystyle A=(6+12{\sqrt {3}})a^{2}\approx 26.7846a^{2}.}$$

3D model of a truncated octahedron

The truncated octahedron is one of the thirteen Archimedean solids. In other words, it has a highly symmetric and semi-regular polyhedron with two or more different regular polygonal faces that meet in a vertex.^[3] The dual polyhedron of a truncated octahedron is the tetrakis hexahedron. They both have the same three-dimensional symmetry group as the regular octahedron does, the octahedral symmetry ${\displaystyle \mathrm {O} _{\mathrm {h} }}$.^[4] A square and two hexagons surround each of its vertex, denoting its vertex figure as ${\displaystyle 4\cdot 6^{2}}$.^[5]

The dihedral angle of a truncated octahedron between square-to-hexagon is ${\textstyle \arccos(-1/{\sqrt {3}})\approx 125.26^{\circ }}$, and that between adjacent hexagonal faces is ${\textstyle \arccos(-1/3)\approx 109.47^{\circ }}$.^[6]

The Cartesian coordinates of the vertices of a truncated octahedron with edge length 1 are all permutations of^[7] $${\displaystyle {\bigl (}\pm {\sqrt {2}},\pm {\tfrac {\sqrt {2}}{2}},0{\bigr )}.}$$

As a space-filling polyhedron

Truncated octahedron as a permutahedron of order 4

Truncated octahedra tiling space

The truncated octahedron can be described as a permutohedron of order 4 or 4-permutohedron, meaning it can be represented with even more symmetric coordinates in four dimensions: all permutations of ${\displaystyle (1,2,3,4)}$ form the vertices of a truncated octahedron in the three-dimensional subspace ${\displaystyle x+y+z+w=10}$.^[8] Therefore, each vertex corresponds to a permutation of ${\displaystyle (1,2,3,4)}$ and each edge represents a single pairwise swap of two elements.^[9] With this labeling, the swaps are of elements whose values differ by one. If, instead, the truncated octahedron is labeled by the inverse permutations, the edges correspond to swaps of elements whose positions differ by one. With this alternative labeling, the edges and vertices of the truncated octahedron form the Cayley graph of the symmetric group ${\displaystyle S_{4}}$, the group of four-element permutations, as generated by swaps of consecutive positions.^[10]

The truncated octahedron can tile space. It is classified as plesiohedron, meaning it can be defined as the Voronoi cell of a symmetric Delone set.^[11] Plesiohedra, translated without rotating, can be repeated to fill space. There are five three-dimensional primary parallelohedrons, one of which is the truncated octahedron. This polyhedron is generated from six line segments with four triples of coplanar segments, with the most symmetric form being generated from six line segments parallel to the face diagonals of a cube;^[12] an example of the honeycomb is the bitruncated cubic honeycomb.^[13] More generally, every permutohedron and parallelohedron is a zonohedron, a polyhedron that is centrally symmetric and can be defined by a Minkowski sum.^[14]

Applications

The structure of the faujasite framework

First Brillouin zone of FCC lattice, showing symmetry labels for high symmetry lines and points.

In chemistry, the truncated octahedron is the sodalite cage structure in the framework of a faujasite-type of zeolite crystals.^[15]

In solid-state physics, the first Brillouin zone of the face-centered cubic lattice is a truncated octahedron.^[16]

The truncated octahedron (in fact, the generalized truncated octahedron) appears in the error analysis of quantization index modulation (QIM) in conjunction with repetition coding.^[17]

Dissection

The truncated octahedron can be dissected into a central octahedron, surrounded by 8 triangular cupolae on each face, and 6 square pyramids above the vertices.^[18]

Second and third genus toroids

Removing the central octahedron and 2 or 4 triangular cupolae creates two Stewart toroids, with dihedral and tetrahedral symmetry:

It is possible to slice a tesseract by a hyperplane so that its sliced cross-section is a truncated octahedron.^[19]

The cell-transitive bitruncated cubic honeycomb can also be seen as the Voronoi tessellation of the body-centered cubic lattice. The truncated octahedron is one of five three-dimensional primary parallelohedra.

Objects

Jungle gym nets often include truncated octahedra.

• 
  ancient Chinese die
• 
  sculpture in Bonn
• 
  Rubik's Cube variant
• 
  model made with Polydron construction set
• 
  Pyrite crystal
• 
  Boleite crystal

Truncated octahedral graph

Truncated octahedral graph
3-fold symmetric Schlegel diagram
Vertices	24
Edges	36
Automorphisms	48
Chromatic number	2
Book thickness	3
Queue number	2
Properties	Cubic, Hamiltonian, regular, zero-symmetric
Table of graphs and parameters

In the mathematical field of graph theory, a truncated octahedral graph is the graph of vertices and edges of the truncated octahedron. It has 24 vertices and 36 edges, and is a cubic Archimedean graph.^[20] It has book thickness 3 and queue number 2.^[21]

As a Hamiltonian cubic graph, it can be represented by LCF notation in multiple ways: [3, −7, 7, −3]⁶, [5, −11, 11, 7, 5, −5, −7, −11, 11, −5, −7, 7]², and [−11, 5, −3, −7, −9, 3, −5, 5, −3, 9, 7, 3, −5, 11, −3, 7, 5, −7, −9, 9, 7, −5, −7, 3].^[22]

Three different Hamiltonian cycles described by the three different LCF notations for the truncated octahedral graph