Steric 5-cubes
From Wikipedia, the free encyclopedia
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cube
| Steric 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 480 |
| Faces | 720 |
| Edges | 400 |
| Vertices | 80 |
| Vertex figure | {3,3}-t1{3,3} antiprism |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
Alternate names
- Steric penteract, runcinated demipenteract
- Small prismated hemipenteract (siphin) (Jonathan Bowers)[1]: (x3o3o *b3o3x - siphin)
Cartesian coordinates
The Cartesian coordinates for the 80 vertices of a steric 5-cube centered at the origin are the permutations of
- (±1,±1,±1,±1,±3)
with an odd number of plus signs.
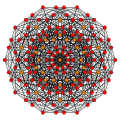
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph |  |
 |
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph |  |
 |
| Dihedral symmetry | [4] | [4] |
Related polytopes
Stericantic 5-cube
| Stericantic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 720 |
| Faces | 1840 |
| Edges | 1680 |
| Vertices | 480 |
| Vertex figure | |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
Alternate names
- Prismatotruncated hemipenteract (pithin) (Jonathan Bowers)[1]: (x3x3o *b3o3x - pithin)
Cartesian coordinates
The Cartesian coordinates for the 480 vertices of a stericantic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±3,±3,±5)
with an odd number of plus signs.
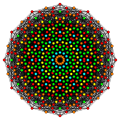
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph |  |
 |
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph |  |
 |
| Dihedral symmetry | [4] | [4] |
Steriruncic 5-cube
| Steriruncic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 560 |
| Faces | 1280 |
| Edges | 1120 |
| Vertices | 320 |
| Vertex figure | |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
Alternate names
- Prismatorhombated hemipenteract (pirhin) (Jonathan Bowers)[1]: (x3o3o *b3x3x - pirhin)
Cartesian coordinates
The Cartesian coordinates for the 320 vertices of a steriruncic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±3,±5)
with an odd number of plus signs.
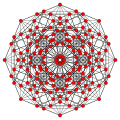
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph |  |
 |
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph |  |
 |
| Dihedral symmetry | [4] | [4] |
Steriruncicantic 5-cube
| Steriruncicantic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 720 |
| Faces | 2080 |
| Edges | 2400 |
| Vertices | 960 |
| Vertex figure | |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
Alternate names
- Great prismated hemipenteract (giphin) (Jonathan Bowers)[1]: (x3x3o *b3x3x - giphin)
Cartesian coordinates
The Cartesian coordinates for the 960 vertices of a steriruncicantic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±3,±5,±7)
with an odd number of plus signs.
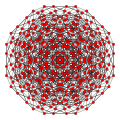
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph |  |
 |
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph |  |
 |
| Dihedral symmetry | [4] | [4] |
Related polytopes
This polytope is based on the 5-demicube, a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
There are 23 uniform polytera (uniform 5-polytope) that can be constructed from the D5 symmetry of the 5-demicube, of which are unique to this family, and 15 are shared within the 5-cube family.
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.