Scalar projection

In mathematics, the scalar projection of a vector ${\displaystyle \mathbf {a} }$ on (or onto) a vector ${\displaystyle \mathbf {b} ,}$ also known as the scalar resolute of ${\displaystyle \mathbf {a} }$ in the direction of ${\displaystyle \mathbf {b} ,}$ is given by:

${\displaystyle s=\left\|\mathbf {a} \right\|\cos \theta =\mathbf {a} \cdot \mathbf {\hat {b}} ,}$

If 0° ≤ θ ≤ 90°, as in this case, the scalar projection of a on b coincides with the length of the vector projection.

Vector projection of a on b (a₁), and vector rejection of a from b (a₂).

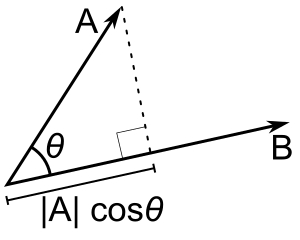
where the operator ${\displaystyle \cdot }$ denotes a dot product, ${\displaystyle {\hat {\mathbf {b} }}}$ is the unit vector in the direction of ${\displaystyle \mathbf {b} ,}$ ${\displaystyle \left\|\mathbf {a} \right\|}$ is the length of ${\displaystyle \mathbf {a} ,}$ and ${\displaystyle \theta }$ is the angle between ${\displaystyle \mathbf {a} }$ and ${\displaystyle \mathbf {b} }$.^[1]

The term scalar component refers sometimes to scalar projection, as, in Cartesian coordinates, the components of a vector are the scalar projections in the directions of the coordinate axes.

The scalar projection is a scalar, equal to the length of the orthogonal projection of ${\displaystyle \mathbf {a} }$ on ${\displaystyle \mathbf {b} }$, with a negative sign if the projection has an opposite direction with respect to ${\displaystyle \mathbf {b} }$.

Multiplying the scalar projection of ${\displaystyle \mathbf {a} }$ on ${\displaystyle \mathbf {b} }$ by ${\displaystyle \mathbf {\hat {b}} }$ converts it into the above-mentioned orthogonal projection, also called vector projection of ${\displaystyle \mathbf {a} }$ on ${\displaystyle \mathbf {b} }$.

Definition based on angle θ

If the angle ${\displaystyle \theta }$ between ${\displaystyle \mathbf {a} }$ and ${\displaystyle \mathbf {b} }$ is known, the scalar projection of ${\displaystyle \mathbf {a} }$ on ${\displaystyle \mathbf {b} }$ can be computed using

${\displaystyle s=\left\|\mathbf {a} \right\|\cos \theta .}$ (${\displaystyle s=\left\|\mathbf {a} _{1}\right\|}$ in the figure)

The formula above can be inverted to obtain the angle, θ.

Definition in terms of a and b

When ${\displaystyle \theta }$ is not known, the cosine of ${\displaystyle \theta }$ can be computed in terms of ${\displaystyle \mathbf {a} }$ and ${\displaystyle \mathbf {b} ,}$ by the following property of the dot product ${\displaystyle \mathbf {a} \cdot \mathbf {b} }$:

${\displaystyle {\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|}}=\cos \theta }$

By this property, the definition of the scalar projection ${\displaystyle s}$ becomes:

${\displaystyle s=\left\|\mathbf {a} _{1}\right\|=\left\|\mathbf {a} \right\|\cos \theta =\left\|\mathbf {a} \right\|{\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|}}={\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {b} \right\|}}\,}$

Properties

The scalar projection has a negative sign if ${\displaystyle 90^{\circ }<\theta \leq 180^{\circ }}$. It coincides with the length of the corresponding vector projection if the angle is smaller than 90°. More exactly, if the vector projection is denoted ${\displaystyle \mathbf {a} _{1}}$ and its length ${\displaystyle \left\|\mathbf {a} _{1}\right\|}$:

${\displaystyle s=\left\|\mathbf {a} _{1}\right\|}$ if ${\displaystyle 0^{\circ }\leq \theta \leq 90^{\circ },}$

${\displaystyle s=-\left\|\mathbf {a} _{1}\right\|}$ if ${\displaystyle 90^{\circ }<\theta \leq 180^{\circ }.}$

See also

• Scalar product
• Cross product
• Vector projection

Sources

• Dot products - www.mit.org
• Scalar projection - Flexbooks.ck12.org
• Scalar Projection & Vector Projection - medium.com
• Lesson Explainer: Scalar Projection | Nagwa

References

1. Strang, Gilbert (2016). Introduction to linear algebra (5th ed.). Wellesley: Cambridge press. ISBN 978-0-9802327-7-6.