Square tiling honeycomb

See also: Order-4 square tiling honeycomb

In the geometry of hyperbolic 3-space, the square tiling honeycomb is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells, whose vertices exist on horospheres and converge to a single ideal point at infinity. Given by Schläfli symbol {4,4,3}, it has three square tilings, {4,4}, around each edge, and six square tilings around each vertex, in a cubic {4,3} vertex figure.^[1]

Square tiling honeycomb
Type	Hyperbolic regular honeycomb Paracompact uniform honeycomb
Schläfli symbols	{4,4,3} r{4,4,4} {41,1,1}
Coxeter diagrams	↔ ↔ ↔
Cells	{4,4}
Faces	square {4}
Edge figure	triangle {3}
Vertex figure	cube, {4,3}
Dual	Order-4 octahedral honeycomb
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3] ${\displaystyle {\overline {N}}_{3}}$, [43] ${\displaystyle {\overline {M}}_{3}}$, [41,1,1]
Properties	Regular

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

Rectified order-4 square tiling

It is also seen as a rectified order-4 square tiling honeycomb, r{4,4,4}:

{4,4,4}	r{4,4,4} = {4,4,3}
	=

Symmetry

The square tiling honeycomb has three reflective symmetry constructions: as a regular honeycomb, a half symmetry construction ↔ , and lastly a construction with three types (colors) of checkered square tilings ↔ .

It also contains an index 6 subgroup [4,4,3^*] ↔ [4^1,1,1], and a radial subgroup [4,(4,3)^*] of index 48, with a right dihedral-angled octahedral fundamental domain, and four pairs of ultraparallel mirrors: .

This honeycomb contains that tile 2-hypercycle surfaces, which are similar to the paracompact order-3 apeirogonal tiling :

Related polytopes and honeycombs

The square tiling honeycomb is a regular hyperbolic honeycomb in 3-space. It is one of eleven regular paracompact honeycombs.

11 paracompact regular honeycombs
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

There are fifteen uniform honeycombs in the [4,4,3] Coxeter group family, including this regular form, and its dual, the order-4 octahedral honeycomb, {3,4,4}.

[4,4,3] family honeycombs

{4,4,3}	r{4,4,3}	t{4,4,3}	rr{4,4,3}	t0,3{4,4,3}	tr{4,4,3}	t0,1,3{4,4,3}	t0,1,2,3{4,4,3}
{3,4,4}	r{3,4,4}	t{3,4,4}	rr{3,4,4}	2t{3,4,4}	tr{3,4,4}	t0,1,3{3,4,4}	t0,1,2,3{3,4,4}

The square tiling honeycomb is part of the order-4 square tiling honeycomb family, as it can be seen as a rectified order-4 square tiling honeycomb.

[4,4,4] family honeycombs
{4,4,4}	r{4,4,4}	t{4,4,4}	rr{4,4,4}	t0,3{4,4,4}	2t{4,4,4}	tr{4,4,4}	t0,1,3{4,4,4}	t0,1,2,3{4,4,4}

It is related to the 24-cell, {3,4,3}, which also has a cubic vertex figure. It is also part of a sequence of honeycombs with square tiling cells:

{4,4,p} honeycombs v t e
Space	E3	H3
Form	Affine	Paracompact		Noncompact
Name	{4,4,2}	{4,4,3}	{4,4,4}	{4,4,5}	{4,4,6}	...{4,4,∞}
Coxeter
Image
Vertex figure	{4,2}	{4,3}	{4,4}	{4,5}	{4,6}	{4,∞}

Rectified square tiling honeycomb

Rectified square tiling honeycomb
Type	Paracompact uniform honeycomb Semiregular honeycomb
Schläfli symbols	r{4,4,3} or t1{4,4,3} 2r{3,41,1} r{41,1,1}
Coxeter diagrams	↔ ↔ ↔
Cells	{4,3} r{4,4}
Faces	square {4}
Vertex figure	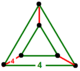triangular prism
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3] ${\displaystyle {\overline {O}}_{3}}$, [3,41,1] ${\displaystyle {\overline {M}}_{3}}$, [41,1,1]
Properties	Vertex-transitive, edge-transitive

The rectified square tiling honeycomb, t₁{4,4,3}, has cube and square tiling facets, with a triangular prism vertex figure.

It is similar to the 2D hyperbolic uniform triapeirogonal tiling, r{∞,3}, with triangle and apeirogonal faces.

Truncated square tiling honeycomb

Truncated square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	t{4,4,3} or t0,1{4,4,3}
Coxeter diagrams	↔ ↔
Cells	{4,3} t{4,4}
Faces	square {4} octagon {8}
Vertex figure	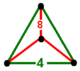triangular pyramid
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3] ${\displaystyle {\overline {N}}_{3}}$, [43] ${\displaystyle {\overline {M}}_{3}}$, [41,1,1]
Properties	Vertex-transitive

The truncated square tiling honeycomb, t{4,4,3}, has cube and truncated square tiling facets, with a triangular pyramid vertex figure. It is the same as the cantitruncated order-4 square tiling honeycomb, tr{4,4,4}, .

Bitruncated square tiling honeycomb

Bitruncated square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	2t{4,4,3} or t1,2{4,4,3}
Coxeter diagram
Cells	t{4,3} t{4,4}
Faces	triangle {3} square {4} octagon {8}
Vertex figure	digonal disphenoid
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Properties	Vertex-transitive

The bitruncated square tiling honeycomb, 2t{4,4,3}, has truncated cube and truncated square tiling facets, with a digonal disphenoid vertex figure.

Cantellated square tiling honeycomb

Cantellated square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	rr{4,4,3} or t0,2{4,4,3}
Coxeter diagrams	↔
Cells	r{4,3} rr{4,4} {}x{3}
Faces	triangle {3} square {4}
Vertex figure	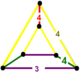isosceles triangular prism
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Properties	Vertex-transitive

The cantellated square tiling honeycomb, rr{4,4,3}, has cuboctahedron, square tiling, and triangular prism facets, with an isosceles triangular prism vertex figure.

Cantitruncated square tiling honeycomb

Cantitruncated square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	tr{4,4,3} or t0,1,2{4,4,3}
Coxeter diagram
Cells	t{4,3} tr{4,4} {}x{3}
Faces	triangle {3} square {4} octagon {8}
Vertex figure	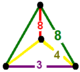isosceles triangular pyramid
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Properties	Vertex-transitive

The cantitruncated square tiling honeycomb, tr{4,4,3}, has truncated cube, truncated square tiling, and triangular prism facets, with an isosceles triangular pyramid vertex figure.

Runcinated square tiling honeycomb

Runcinated square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,3{4,4,3}
Coxeter diagrams	↔
Cells	{3,4} {4,4} {}x{4} {}x{3}
Faces	triangle {3} square {4}
Vertex figure	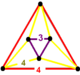irregular triangular antiprism
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Properties	Vertex-transitive

The runcinated square tiling honeycomb, t_0,3{4,4,3}, has octahedron, triangular prism, cube, and square tiling facets, with an irregular triangular antiprism vertex figure.

Runcitruncated square tiling honeycomb

Runcitruncated square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	t0,1,3{4,4,3} s2,3{3,4,4}
Coxeter diagrams
Cells	rr{4,3} t{4,4} {}x{3} {}x{8}
Faces	triangle {3} square {4} octagon {8}
Vertex figure	isosceles-trapezoidal pyramid
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Properties	Vertex-transitive

The runcitruncated square tiling honeycomb, t_0,1,3{4,4,3}, has rhombicuboctahedron, octagonal prism, triangular prism and truncated square tiling facets, with an isosceles-trapezoidal pyramid vertex figure.

Runcicantellated square tiling honeycomb

The runcicantellated square tiling honeycomb is the same as the runcitruncated order-4 octahedral honeycomb.

Omnitruncated square tiling honeycomb

Omnitruncated square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,1,2,3{4,4,3}
Coxeter diagram
Cells	tr{4,4} {}x{6} {}x{8} tr{4,3}
Faces	square {4} hexagon {6} octagon {8}
Vertex figure	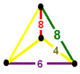irregular tetrahedron
Coxeter groups	${\displaystyle {\overline {R}}_{3}}$, [4,4,3]
Properties	Vertex-transitive

The omnitruncated square tiling honeycomb, t_0,1,2,3{4,4,3}, has truncated square tiling, truncated cuboctahedron, hexagonal prism, and octagonal prism facets, with an irregular tetrahedron vertex figure.

Omnisnub square tiling honeycomb

Omnisnub square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	h(t0,1,2,3{4,4,3})
Coxeter diagram
Cells	sr{4,4} sr{2,3} sr{2,4} sr{4,3}
Faces	triangle {3} square {4}
Vertex figure	irregular tetrahedron
Coxeter group	[4,4,3]+
Properties	Non-uniform, vertex-transitive

The alternated omnitruncated square tiling honeycomb (or omnisnub square tiling honeycomb), h(t_0,1,2,3{4,4,3}), has snub square tiling, snub cube, triangular antiprism, square antiprism, and tetrahedron cells, with an irregular tetrahedron vertex figure.

Alternated square tiling honeycomb

Alternated square tiling honeycomb
Type	Paracompact uniform honeycomb Semiregular honeycomb
Schläfli symbol	h{4,4,3} hr{4,4,4} {(4,3,3,4)} h{41,1,1}
Coxeter diagrams	↔ ↔ ↔ ↔ ↔ ↔
Cells	{4,4} {4,3}
Faces	square {4}
Vertex figure	cuboctahedron
Coxeter groups	${\displaystyle {\overline {O}}_{3}}$, [3,41,1] [4,1+,4,4] ↔ [∞,4,4,∞] ${\displaystyle {\widehat {BR}}_{3}}$, [(4,4,3,3)] [1+,41,1,1] ↔ [∞[6]]
Properties	Vertex-transitive, edge-transitive, quasiregular

The alternated square tiling honeycomb, h{4,4,3}, is a quasiregular paracompact uniform honeycomb in hyperbolic 3-space. It has cube and square tiling facets in a cuboctahedron vertex figure.

Cantic square tiling honeycomb

Cantic square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	h2{4,4,3}
Coxeter diagrams	↔
Cells	t{4,4} r{4,3} t{4,3}
Faces	triangle {3} square {4} octagon {8}
Vertex figure	rectangular pyramid
Coxeter groups	${\displaystyle {\overline {O}}_{3}}$, [3,41,1]
Properties	Vertex-transitive

The cantic square tiling honeycomb, h₂{4,4,3}, is a paracompact uniform honeycomb in hyperbolic 3-space. It has truncated square tiling, truncated cube, and cuboctahedron facets, with a rectangular pyramid vertex figure.

Runcic square tiling honeycomb

Runcic square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	h3{4,4,3}
Coxeter diagrams	↔
Cells	{4,4} r{4,3} {3,4}
Faces	triangle {3} square {4}
Vertex figure	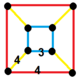square frustum
Coxeter groups	${\displaystyle {\overline {O}}_{3}}$, [3,41,1]
Properties	Vertex-transitive

The runcic square tiling honeycomb, h₃{4,4,3}, is a paracompact uniform honeycomb in hyperbolic 3-space. It has square tiling, rhombicuboctahedron, and octahedron facets in a square frustum vertex figure.

Runcicantic square tiling honeycomb

Runcicantic square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	h2,3{4,4,3}
Coxeter diagrams	↔
Cells	t{4,4} tr{4,3} t{3,4}
Faces	square {4} hexagon {6} octagon {8}
Vertex figure	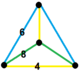mirrored sphenoid
Coxeter groups	${\displaystyle {\overline {O}}_{3}}$, [3,41,1]
Properties	Vertex-transitive

The runcicantic square tiling honeycomb, h_2,3{4,4,3}, ↔ , is a paracompact uniform honeycomb in hyperbolic 3-space. It has truncated square tiling, truncated cuboctahedron, and truncated octahedron facets in a mirrored sphenoid vertex figure.

Alternated rectified square tiling honeycomb

Alternated rectified square tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	hr{4,4,3}
Coxeter diagrams	↔
Cells
Faces
Vertex figure	triangular prism
Coxeter groups	[4,1+,4,3] = [∞,3,3,∞]
Properties	Nonsimplectic, vertex-transitive

The alternated rectified square tiling honeycomb is a paracompact uniform honeycomb in hyperbolic 3-space.

See also

• Convex uniform honeycombs in hyperbolic space
• Regular tessellations of hyperbolic 3-space
• Paracompact uniform honeycombs