Runcic 7-cubes

In seven-dimensional geometry, a runcic 7-cube is a convex uniform 7-polytope, related to the uniform 7-demicube. There are 2 unique forms.

7-demicube	Runcic 7-cube	Runcicantic 7-cube
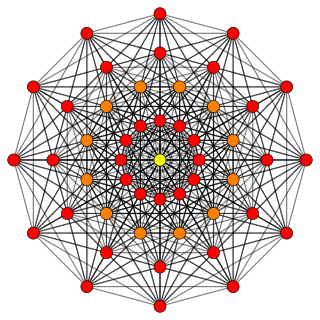
Orthogonal projections in D7 Coxeter plane

Runcic 7-cube

Runcic 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,2{3,34,1} h3{4,35}
Coxeter-Dynkin diagram
5-faces
4-faces
Cells
Faces
Edges	16800
Vertices	2240
Vertex figure
Coxeter groups	D7, [34,1,1]
Properties	convex

A runcic 7-cube, h₃{4,3⁵}, has half the vertices of a runcinated 7-cube, t_0,3{4,3⁵}.

Alternate names

• Small rhombated hemihepteract (Acronym sirhesa) (Jonathan Bowers)^[1]

Cartesian coordinates

The Cartesian coordinates for the vertices of a cantellated demihepteract centered at the origin are coordinate permutations:

(±1,±1,±1,±3,±3,±3,±3)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B7	D7	D6
Graph
Dihedral symmetry	[14/2]	[12]	[10]
Coxeter plane	D5	D4	D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Runcicantic 7-cube

Runcicantic 7-cube
Type	uniform 7-polytope
Schläfli symbol	t0,1,2{3,34,1} h2,3{4,35}
Coxeter-Dynkin diagram
5-faces
4-faces
Cells
Faces
Edges	23520
Vertices	6720
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

A runcicantic 7-cube, h_2,3{4,3⁵}, has half the vertices of a runcicantellated 7-cube, t_0,1,3{4,3⁵}.

Alternate names

• Great rhombated hemihepteract (Acronym girhesa) (Jonathan Bowers)^[2]

Cartesian coordinates

The Cartesian coordinates for the vertices of a runcicantic 7-cube centered at the origin are coordinate permutations:

(±1,±1,±1,±1,±3,±5,±5)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B7	D7	D6
Graph
Dihedral symmetry	[14/2]	[12]	[10]
Coxeter plane	D5	D4	D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Related polytopes

This polytope is based on the 7-demicube, a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.

There are 95 uniform polytopes with D₇ symmetry, 63 are shared by the BC₆ symmetry, and 32 are unique:

D7 polytopes
t0(141)	t0,1(141)	t0,2(141)	t0,3(141)	t0,4(141)	t0,5(141)	t0,1,2(141)	t0,1,3(141)
t0,1,4(141)	t0,1,5(141)	t0,2,3(141)	t0,2,4(141)	t0,2,5(141)	t0,3,4(141)	t0,3,5(141)	t0,4,5(141)
t0,1,2,3(141)	t0,1,2,4(141)	t0,1,2,5(141)	t0,1,3,4(141)	t0,1,3,5(141)	t0,1,4,5(141)	t0,2,3,4(141)	t0,2,3,5(141)
t0,2,4,5(141)	t0,3,4,5(141)	t0,1,2,3,4(141)	t0,1,2,3,5(141)	t0,1,2,4,5(141)	t0,1,3,4,5(141)	t0,2,3,4,5(141)	t0,1,2,3,4,5(141)