Hexic 7-cubes
From Wikipedia, the free encyclopedia
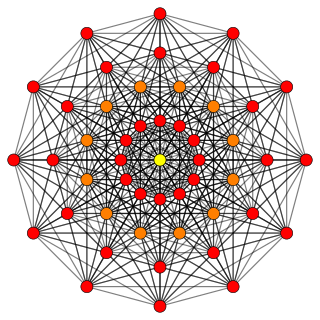
In seven-dimensional geometry, a hexic 7-cube is a convex uniform 7-polytope, constructed from the uniform 7-demicube. There are 16 unique forms.
 7-demicube |
 Hexic 7-cube |
 Hexicantic 7-cube |
 Hexiruncic 7-cube |
 Hexiruncicantic 7-cube |
 Hexisteric 7-cube |
 Hexistericantic 7-cube |
 Hexisteriruncic 7-cube |
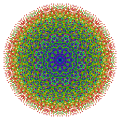 Hexisteriruncicantic 7-cube |
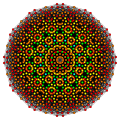 Hexipentic 7-cube |
 Hexipenticantic 7-cube |
 Hexipentiruncic 7-cube |
 Hexipentiruncicantic 7-cube |
 Hexipentisteric 7-cube |
 Hexipentistericantic 7-cube |
 Hexipentisteriruncic 7-cube |
 Hexipentisteriruncicantic 7-cube |
|||
| Orthogonal projections in D7 Coxeter plane | ||||
|---|---|---|---|---|
Hexic 7-cube
| Hexic 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,5{3,34,1} h6{4,35} |
| Coxeter-Dynkin diagram | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 4704 |
| Vertices | 448 |
| Vertex figure | |
| Coxeter groups | D7, [34,1,1] |
| Properties | convex |
Cartesian coordinates
The Cartesian coordinates for the vertices of a hexic 7-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±1,±1,±1,±3)
with an odd number of plus signs.
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph | 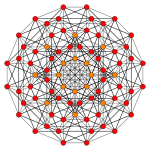 |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexicantic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
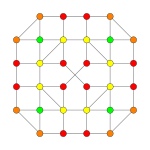 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexiruncic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexisteric 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexipentic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexiruncicantic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexistericantic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexipenticantic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexisteriruncic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexipentiruncic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexipentisteric 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexisteriruncicantic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
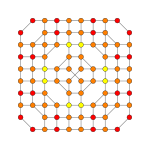
Hexipentiruncicantic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexipentisteriruncic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexipentistericantic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Hexipentisteriruncicantic 7-cube
Images
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph |  |
 |
 |
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph |  |
 | |
| Dihedral symmetry |
[6] | [4] |
Related polytopes
This polytope is based on the 7-demicube, a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
There are 95 uniform polytopes with D7 symmetry, 63 are shared by the BC7 symmetry, and 32 are unique:
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.