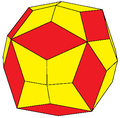
Rectified truncated octahedron

In geometry, the rectified truncated octahedron is a convex polyhedron, constructed as a rectified, truncated octahedron. It has 38 faces: 24 isosceles triangles, 6 squares, and 8 hexagons.

Rectified truncated octahedron
Faces	38: 24 isosceles triangles 6 squares 8 hexagons
Edges	72
Vertices	12+24
Schläfli symbol	rt{3,4}
Conway notation	atO
Symmetry group	Oh, [4,3], (*432), order 48
Rotation group	O, [4,3]+, (432), order 24
Dual polyhedron	Joined truncated octahedron
Properties	convex
Net

Topologically, the squares corresponding to the octahedron's vertices are always regular, although the hexagons, while having equal edge lengths, do not have the same edge lengths with the squares, having different but alternating angles, causing the triangles to be isosceles instead.

Related polyhedra

The rectified truncated octahedron can be seen in sequence of rectification and truncation operations from the octahedron. Further truncation, and alternation creates two more polyhedra:

Name	Truncated octahedron	Rectified truncated octahedron	Truncated rectified truncated octahedron	Snub rectified truncated octahedron
Coxeter	tO	rtO	trtO	srtO
Conway		atO	btO	stO
Image
Conway	dtO = kC	jtO	mtO	mtO
Dual

See also

• Rectified truncated tetrahedron
• Rectified truncated cube
• Rectified truncated dodecahedron
• Rectified truncated icosahedron