Pythagorean interval

In musical tuning theory, a Pythagorean interval is a musical interval with a frequency ratio equal to a power of two divided by a power of three, or vice versa.^[1] For instance, the perfect fifth with ratio 3/2 (equivalent to 3¹/ 2¹) and the perfect fourth with ratio 4/3 (equivalent to 2²/ 3¹) are Pythagorean intervals.

Pythagorean perfect fifth on C Play^ⓘ: C-G (3/2 ÷ 1/1 = 3/2).

All the intervals between the notes of a scale are Pythagorean if they are tuned using the Pythagorean tuning system. However, some Pythagorean intervals are also used in other tuning systems. For instance, the above-mentioned Pythagorean perfect fifth and fourth are also used in just intonation.

Interval table

Name	Short	Other name(s)	Ratio	Factors	Derivation	Cents	ET Cents	MIDI file	Fifths
diminished second	d2		524288/531441	219/312		−23.460	0	playⓘ	−12
(perfect) unison	P1		1/1	30/20	1/1	0.000	0	playⓘ	0
Pythagorean comma			531441/524288	312/219		23.460	0	playⓘ	12
minor second	m2	limma, diatonic semitone, minor semitone	256/243	28/35		90.225	100	playⓘ	−5
augmented unison	A1	apotome, chromatic semitone, major semitone	2187/2048	37/211		113.685	100	playⓘ	7
diminished third	d3	tone, whole tone, whole step	65536/59049	216/310		180.450	200	playⓘ	−10
major second	M2		9/8	32/23	3·3/2·2	203.910	200	playⓘ	2
semiditone	m3	(Pythagorean minor third)	32/27	25/33		294.135	300	playⓘ	−3
augmented second	A2		19683/16384	39/214		317.595	300	playⓘ	9
diminished fourth	d4		8192/6561	213/38		384.360	400	playⓘ	−8
ditone	M3	(Pythagorean major third)	81/64	34/26	27·3/32·2	407.820	400	playⓘ	4
perfect fourth	P4	diatessaron, sesquitertium	4/3	22/3	2·2/3	498.045	500	playⓘ	−1
augmented third	A3		177147/131072	311/217		521.505	500	playⓘ	11
diminished fifth	d5	tritone	1024/729	210/36		588.270	600	playⓘ	−6
augmented fourth	A4		729/512	36/29		611.730	600	playⓘ	6
diminished sixth	d6		262144/177147	218/311		678.495	700	playⓘ	−11
perfect fifth	P5	diapente, sesquialterum	3/2	31/21	3/2	701.955	700	playⓘ	1
minor sixth	m6		128/81	27/34		792.180	800	playⓘ	−4
augmented fifth	A5		6561/4096	38/212		815.640	800	playⓘ	8
diminished seventh	d7		32768/19683	215/39		882.405	900	playⓘ	−9
major sixth	M6		27/16	33/24	9·3/8·2	905.865	900	playⓘ	3
minor seventh	m7		16/9	24/32		996.090	1000	playⓘ	−2
augmented sixth	A6		59049/32768	310/215		1019.550	1000	playⓘ	10
diminished octave	d8		4096/2187	212/37		1086.315	1100	playⓘ	−7
major seventh	M7		243/128	35/27	81·3/64·2	1109.775	1100	playⓘ	5
diminished ninth	d9	(octave − comma)	1048576/531441	220/312		1176.540	1200	playⓘ	−12
(perfect) octave	P8	diapason	2/1		2/1	1200.000	1200	playⓘ	0
augmented seventh	A7	(octave + comma)	531441/262144	312/218		1223.460	1200	playⓘ	12

Notice that the terms ditone and semiditone are specific for Pythagorean tuning, while tone and tritone are used generically for all tuning systems. Despite its name, a semiditone (3 semitones, or about 300 cents) can hardly be viewed as half of a ditone (4 semitones, or about 400 cents).

Frequency ratio of the 144 intervals in D-based Pythagorean tuning. Interval names are given in their shortened form. Pure intervals are shown in bold font. Wolf intervals are highlighted in red. Numbers larger than 999 are shown as powers of 2 or 3. Other versions of this table are provided here and here.

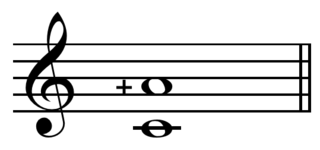
12-tone Pythagorean scale

The table shows from which notes some of the above listed intervals can be played on an instrument using a repeated-octave 12-tone scale (such as a piano) tuned with D-based symmetric Pythagorean tuning. Further details about this table can be found in Size of Pythagorean intervals.

Pythagorean perfect fifth on D Play^ⓘ: D-A+ (27/16 ÷ 9/8 = 3/2).

Just perfect fourth Play^ⓘ, one perfect fifth inverted (4/3 ÷ 1/1 = 4/3).

Major tone on C Play^ⓘ: C-D (9/8 ÷ 3/2 = 3/2), two Pythagorean perfect fifths.

Pythagorean small minor seventh (1/1 - 16/9) Play^ⓘ, two perfect fifths inverted.

Pythagorean major sixth on C (1/1 - 27/16) Play^ⓘ, three Pythagorean perfect fifths.

Semiditone on C (1/1 - 32/27) Play^ⓘ, three Pythagorean perfect fifths inverted.

Ditone on C (1/1 - 81/64) Play^ⓘ, four Pythagorean perfect fifths.

Pythagorean minor sixth on C (1/1 - 128/81) Play^ⓘ, four Pythagorean perfect fifths inverted.

Pythagorean major seventh on C (1/1 - 243/128) Play^ⓘ, five Pythagorean perfect fifths.

Pythagorean augmented fourth tritone on C (1/1 - 729/512) Play^ⓘ, six Pythagorean perfect fifths.

Pythagorean diminished fifth tritone on C (1/1 - 1024/729) Play^ⓘ, six Pythagorean perfect fifths inverted.

Fundamental intervals

The fundamental intervals are the superparticular ratios 2/1, 3/2, and 4/3. 2/1 is the octave or diapason (Greek for "across all"). 3/2 is the perfect fifth, diapente ("across five"), or sesquialterum. 4/3 is the perfect fourth, diatessaron ("across four"), or sesquitertium. These three intervals and their octave equivalents, such as the perfect eleventh and twelfth, are the only absolute consonances of the Pythagorean system. All other intervals have varying degrees of dissonance, ranging from smooth to rough.

The difference between the perfect fourth and the perfect fifth is the tone or major second. This has the ratio 9/8, also known as epogdoon and it is the only other superparticular ratio of Pythagorean tuning, as shown by Størmer's theorem.

Two tones make a ditone, a dissonantly wide major third, ratio 81/64. The ditone differs from the just major third (5/4) by the syntonic comma (81/80). Likewise, the difference between the tone and the perfect fourth is the semiditone, a narrow minor third, 32/27, which differs from 6/5 by the syntonic comma. These differences are "tempered out" or eliminated by using compromises in meantone temperament.

The difference between the minor third and the tone is the minor semitone or limma of 256/243. The difference between the tone and the limma is the major semitone or apotome ("part cut off") of 2187/2048. Although the limma and the apotome are both represented by one step of 12-pitch equal temperament, they are not equal in Pythagorean tuning, and their difference, 531441/524288, is known as the Pythagorean comma.

Contrast with modern nomenclature

There is a one-to-one correspondence between interval names (number of scale steps + quality) and frequency ratios. This contrasts with equal temperament, in which intervals with the same frequency ratio can have different names (e.g., the diminished fifth and the augmented fourth); and with other forms of just intonation, in which intervals with the same name can have different frequency ratios (e.g., 9/8 for the major second from C to D, but 10/9 for the major second from D to E).

Pythagorean diatonic scale on C Play^ⓘ.

See also

• Generated collection
• Just intonation
• List of meantone intervals
• List of intervals in 5-limit just intonation
• Shí-èr-lǜ
• Whole-tone scale