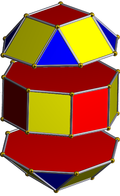
Elongated square gyrobicupola

In geometry, the elongated square gyrobicupola is a polyhedron constructed by two square cupolas attaching onto the bases of octagonal prism, with one of them rotated. It was once mistakenly considered a rhombicuboctahedron by many mathematicians. It is not considered to be an Archimedean solid because it lacks a set of global symmetries that map every vertex to every other vertex, unlike the 13 Archimedean solids. It is also a canonical polyhedron. For this reason, it is also known as pseudo-rhombicuboctahedron, Miller solid,^[1] or Miller–Askinuze solid.^[2]

Elongated square gyrobicupola
Type	Canonical, Johnson J36 – J37 – J38
Faces	8 triangles 18 squares
Edges	48
Vertices	24
Vertex configuration	${\displaystyle 8+16(3\cdot 4^{3})}$
Symmetry group	${\displaystyle D_{4\mathrm {d} }}$
Properties	convex, singular vertex figure
Net

Construction

The elongated square gyrobicupola can be constructed similarly to the rhombicuboctahedron, by attaching two regular square cupolas onto the bases of an octagonal prism, a process known as elongation. The difference between these two polyhedrons is that one of the two square cupolas is twisted by 45 degrees, a process known as gyration, making the triangular faces staggered vertically.^[3][1] The resulting polyhedron has 8 equilateral triangles and 18 squares.^[3] A convex polyhedron in which all of the faces are regular polygons is a Johnson solid, and the elongated square gyrobicupola is among them, enumerated as the 37th Johnson solid ${\displaystyle J_{37}}$.^[4]

Process of the construction of the elongated square gyrobicupola

The elongated square gyrobicupola may have been discovered by Johannes Kepler in his enumeration of the Archimedean solids, but its first clear appearance in print appears to be the work of Duncan Sommerville in 1905.^[5] It was independently rediscovered by J. C. P. Miller in 1930 by mistake while attempting to construct a model of the rhombicuboctahedron. This solid was discovered again by V. G. Ashkinuse in 1957.^[1][6][7]

Properties

An elongated square gyrobicupola with edge length ${\displaystyle a}$ has a surface area:^[3] $${\displaystyle \left(18+2{\sqrt {3}}\right)a^{2}\approx 21.464a^{2},}$$ by adding the area of 8 equilateral triangles and 10 squares. Its volume can be calculated by slicing it into two square cupolas and one octagonal prism:^[3] $${\displaystyle {\frac {12+10{\sqrt {2}}}{3}}a^{3}\approx 8.714a^{3}.}$$

3D model of an elongated square gyrobicupola

The elongated square gyrobicupola possesses three-dimensional symmetry group ${\displaystyle D_{4\mathrm {d} }}$ of order 16. It is locally vertex-regular – the arrangement of the four faces incident on any vertex is the same for all vertices; this is unique among the Johnson solids. However, the manner in which it is "twisted" gives it a distinct "equator" and two distinct "poles", which in turn divides its vertices into 8 "polar" vertices (4 per pole) and 16 "equatorial" vertices. It is therefore not vertex-transitive, and consequently not usually considered to be the 14th Archimedean solid.^[1][7][8]

The dihedral angle of an elongated square gyrobicupola can be ascertained in a similar way as the rhombicuboctahedron, by adding the dihedral angle of a square cupola and an octagonal prism:^[2]

• the dihedral angle of a rhombicuboctahedron between two adjacent squares on both the top and bottom is that of a square cupola 135°. The dihedral angle of an octagonal prism between two adjacent squares is the internal angle of a regular octagon 135°. The dihedral angle between two adjacent squares on the edge where a square cupola is attached to an octagonal prism is the sum of the dihedral angle of a square cupola square-to-octagon and the dihedral angle of an octagonal prism square-to-octagon 45° + 90° = 135°. Therefore, the dihedral angle of a rhombicuboctahedron for every two adjacent squares is 135°.
• the dihedral angle of a rhombicuboctahedron square-to-triangle is that of a square cupola between those, 144.7°. The dihedral angle between square-to-triangle, on the edge where a square cupola is attached to an octagonal prism is the sum of the dihedral angle of a square cupola triangle-to-octagon and the dihedral angle of an octagonal prism square-to-octagon 54.7° + 90° = 144.7°. Therefore, the dihedral angle of a rhombicuboctahedron for every square-to-triangle is 144.7°.

Related polyhedra and honeycombs

The elongated square gyrobicupola can form a space-filling honeycomb with the regular tetrahedron, cube, and cuboctahedron. It can also form another honeycomb with the tetrahedron, square pyramid and various combinations of cubes, elongated square pyramids, and elongated square bipyramids.^[9]

The pseudo great rhombicuboctahedron

The pseudo great rhombicuboctahedron is a nonconvex analog of the pseudo-rhombicuboctahedron, constructed in a similar way from the nonconvex great rhombicuboctahedron.

In chemistry

The polyvanadate ion [V₁₈O₄₂]¹²⁻ has a pseudo-rhombicuboctahedral structure, where each square face acts as the base of a VO₅ pyramid.^[10]

References

1. Cromwell, Peter R. (1997), Polyhedra, Cambridge University Press, p. 91, ISBN 978-0-521-55432-9.
2. Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, S2CID 122006114, Zbl 0132.14603.
3. Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
4. Francis, Darryl (August 2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177.
5. Sommerville, D. M. Y. (1905), "Semi-regular networks of the plane in absolute geometry", Transactions of the Royal Society of Edinburgh, 41: 725–747, doi:10.1017/s0080456800035560. As cited by Grünbaum (2009).
6. Ball, Rouse (1939), Coxeter, H. S. M. (ed.), Mathematical recreations and essays (11 ed.), p. 137.
7. Grünbaum, Branko (2009), "An enduring error" (PDF), Elemente der Mathematik, 64 (3): 89–101, doi:10.4171/EM/120, MR 2520469 Reprinted in Pitici, Mircea, ed. (2011). The Best Writing on Mathematics 2010. Princeton University Press. pp. 18–31..
8. Lando, Sergei K.; Zvonkin, Alexander K. (2004), Graphs on Surfaces and Their Applications, Springer, p. 114, doi:10.1007/978-3-540-38361-1, ISBN 978-3-540-38361-1.
9. "J37 honeycombs", Gallery of Wooden Polyhedra, retrieved 2016-03-21
10. Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. p. 986. ISBN 978-0-08-037941-8.

Further reading

• Anthony Pugh (1976), Polyhedra: A visual approach, California: University of California Press Berkeley, ISBN 0-520-03056-7 Chapter 2: Archimedean polyhedra, prisma and antiprisms, p. 25 Pseudo-rhombicuboctahedron

External links

• Weisstein, Eric W., "Elongated square gyrobicupola" ("Johnson solid") at MathWorld.
• George Hart: pseudo-rhombicuboctahedra