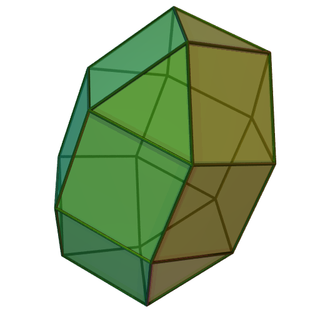
Elongated triangular gyrobicupola

In geometry, the elongated triangular gyrobicupola is a polyhedron constructed by attaching two regular triangular cupolas to the base of a regular hexagonal prism, with one of them rotated in ${\displaystyle 60^{\circ }}$. It is an example of Johnson solid.

Elongated triangular gyrobicupola
Type	Johnson J35 – J36 – J37
Faces	8 triangles 12 squares
Edges	36
Vertices	18
Vertex configuration	${\displaystyle {\begin{aligned}&6\times (3\times 4\times 3\times 4)+\\&12\times (3\times 4^{3})\end{aligned}}}$
Symmetry group	${\displaystyle D_{3h}}$
Properties	convex
Net

Construction

The elongated triangular gyrobicupola is similarly can be constructed as the elongated triangular orthobicupola, started from a hexagonal prism by attaching two regular triangular cupolae onto its base, covering its hexagonal faces.^[1] This construction process is known as elongation, giving the resulting polyhedron has 8 equilateral triangles and 12 squares.^[2] The difference between those two polyhedrons is one of two triangular cupolas in the elongated triangular gyrobicupola is rotated in ${\displaystyle 60^{\circ }}$. A convex polyhedron in which all faces are regular is Johnson solid, and the elongated triangular gyrobicupola is one among them, enumerated as 36th Johnson solid ${\displaystyle J_{36}}$.^[3]

Properties

An elongated triangular gyrobicupola with a given edge length ${\displaystyle a}$ has a surface area by adding the area of all regular faces:^[2] $${\displaystyle \left(12+2{\sqrt {3}}\right)a^{2}\approx 15.464a^{2}.}$$ Its volume can be calculated by cutting it off into two triangular cupolae and a hexagonal prism with regular faces, and then adding their volumes up:^[2] $${\displaystyle \left({\frac {5{\sqrt {2}}}{3}}+{\frac {3{\sqrt {3}}}{2}}\right)a^{3}\approx 4.955a^{3}.}$$

Its three-dimensional symmetry groups is the prismatic symmetry, the dihedral group ${\displaystyle D_{3d}}$ of order 12.^{[clarification needed]} Its dihedral angle can be calculated by adding the angle of the triangular cupola and hexagonal prism. The dihedral angle of a hexagonal prism between two adjacent squares is the internal angle of a regular hexagon ${\displaystyle 120^{\circ }=2\pi /3}$, and that between its base and square face is ${\displaystyle \pi /2=90^{\circ }}$. The dihedral angle of a regular triangular cupola between each triangle and the hexagon is approximately ${\displaystyle 70.5^{\circ }}$, that between each square and the hexagon is ${\displaystyle 54.7^{\circ }}$, and that between square and triangle is ${\displaystyle 125.3^{\circ }}$. The dihedral angle of an elongated triangular orthobicupola between the triangle-to-square and square-to-square, on the edge where the triangular cupola and the prism is attached, is respectively:^[4] $${\displaystyle {\begin{aligned}{\frac {\pi }{2}}+70.5^{\circ }&\approx 160.5^{\circ },\\{\frac {\pi }{2}}+54.7^{\circ }&\approx 144.7^{\circ }.\end{aligned}}}$$

Related polyhedra and honeycombs

The elongated triangular gyrobicupola forms space-filling honeycombs with tetrahedra and square pyramids.^[5]