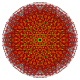
Pentic 6-cubes

In six-dimensional geometry, a pentic 6-cube is a convex uniform 6-polytope.

6-demicube (half 6-cube) =	Pentic 6-cube 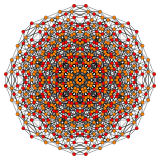=	Penticantic 6-cube =
Pentiruncic 6-cube =	Pentiruncicantic 6-cube =	Pentisteric 6-cube =
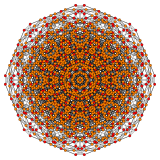Pentistericantic 6-cube =	Pentisteriruncic 6-cube =	Pentisteriruncicantic 6-cube =
Orthogonal projections in D6 Coxeter plane

There are 8 pentic forms of the 6-cube.

Pentic 6-cube

Pentic 6-cube
Type	uniform 6-polytope
Schläfli symbol	t0,4{3,34,1} h5{4,34}
Coxeter-Dynkin diagram	=
5-faces
4-faces
Cells
Faces
Edges	1440
Vertices	192
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

The pentic 6-cube, , has half of the vertices of a pentellated 6-cube, .

Alternate names

• Stericated 6-demicube/demihexeract
• Small cellated hemihexeract (Acronym: sochax) (Jonathan Bowers)^[1]

Cartesian coordinates

The Cartesian coordinates for the vertices, centered at the origin are coordinate permutations:

(±1,±1,±1,±1,±1,±3)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph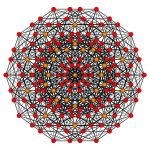
Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph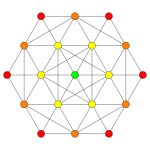
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Penticantic 6-cube

Penticantic 6-cube
Type	uniform 6-polytope
Schläfli symbol	t0,1,4{3,34,1} h2,5{4,34}
Coxeter-Dynkin diagram	=
5-faces
4-faces
Cells
Faces
Edges	9600
Vertices	1920
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

The penticantic 6-cube, , has half of the vertices of a penticantellated 6-cube, .

Alternate names

• Steritruncated 6-demicube/demihexeract
• cellitruncated hemihexeract (Acronym: cathix) (Jonathan Bowers)^[2]

Cartesian coordinates

The Cartesian coordinates for the vertices, centered at the origin are coordinate permutations:

(±1,±1,±3,±3,±3,±5)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph
Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph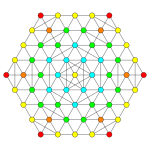
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentiruncic 6-cube

Pentiruncic 6-cube
Type	uniform 6-polytope
Schläfli symbol	t0,2,4{3,34,1} h3,5{4,34}
Coxeter-Dynkin diagram	=
5-faces
4-faces
Cells
Faces
Edges	10560
Vertices	1920
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

The pentiruncic 6-cube, , has half of the vertices of a pentiruncinated 6-cube (penticantellated 6-orthoplex), .

Alternate names

• Stericantellated 6-demicube/demihexeract
• cellirhombated hemihexeract (Acronym: crohax) (Jonathan Bowers)^[3]

Cartesian coordinates

The Cartesian coordinates for the vertices, centered at the origin are coordinate permutations:

(±1,±1,±1,±3,±3,±5)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph
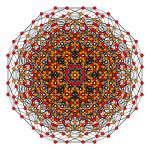Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph
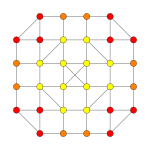Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentiruncicantic 6-cube

Pentiruncicantic 6-cube
Type	uniform 6-polytope
Schläfli symbol	t0,1,2,4{3,32,1} h2,3,5{4,34}
Coxeter-Dynkin diagram	=
5-faces
4-faces
Cells
Faces
Edges	20160
Vertices	5760
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

The pentiruncicantic 6-cube, , has half of the vertices of a pentiruncicantellated 6-cube or (pentiruncicantellated 6-orthoplex),

Alternate names

• Stericantitruncated demihexeract, stericantitruncated 7-demicube
• Great cellated hemihexeract (Acronym: cagrohax) (Jonathan Bowers)^[4]

Cartesian coordinates

The Cartesian coordinates for the vertices, centered at the origin are coordinate permutations:

(±1,±1,±3,±3,±5,±7)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph
Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph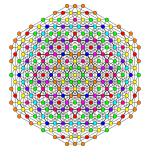
Dihedral symmetry	[6]	[4]

Pentisteric 6-cube

Pentisteric 6-cube
Type	uniform 6-polytope
Schläfli symbol	t0,3,4{3,34,1} h4,5{4,34}
Coxeter-Dynkin diagram	=
5-faces
4-faces
Cells
Faces
Edges	5280
Vertices	960
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

The pentisteric 6-cube, , has half of the vertices of a pentistericated 6-cube (pentitruncated 6-orthoplex),

Alternate names

• Steriruncinated 6-demicube/demihexeract
• Small cellipriamated hemihexeract (Acronym: cophix) (Jonathan Bowers)^[5]

Cartesian coordinates

The Cartesian coordinates for the vertices, centered at the origin are coordinate permutations:

(±1,±1,±1,±1,±3,±5)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph
Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph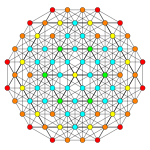
Dihedral symmetry	[6]	[4]

Pentistericantic 6-cube

Pentistericantic 6-cube
Type	uniform 6-polytope
Schläfli symbol	t0,1,3,4{3,34,1} h2,4,5{4,34}
Coxeter-Dynkin diagram	=
5-faces
4-faces
Cells
Faces
Edges	23040
Vertices	5760
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

The pentistericantic 6-cube, , has half of the vertices of a pentistericantellated 6-cube (pentiruncitruncated 6-orthoplex), .

Alternate names

• Steriruncitruncated demihexeract/7-demicube
• cellitruncated hemihexeract (Acronym: capthix) (Jonathan Bowers)^[6]

Cartesian coordinates

The Cartesian coordinates for the vertices, centered at the origin are coordinate permutations:

(±1,±1,±3,±3,±5,±7)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph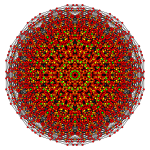
Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentisteriruncic 6-cube

Pentisteriruncic 6-cube
Type	uniform 6-polytope
Schläfli symbol	t0,2,3,4{3,34,1} h3,4,5{4,34}
Coxeter-Dynkin diagram	=
5-faces
4-faces
Cells
Faces
Edges	15360
Vertices	3840
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

The pentisteriruncic 6-cube, , has half of the vertices of a pentisteriruncinated 6-cube (penticantitruncated 6-orthoplex), .

Alternate names

• Steriruncicantellated 6-demicube/demihexeract
• Celliprismatorhombated hemihexeract (Acronym: caprohax) (Jonathan Bowers)^[7]

Cartesian coordinates

The Cartesian coordinates for the vertices, centered at the origin are coordinate permutations:

(±1,±1,±1,±3,±5,±7)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph
Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentisteriruncicantic 6-cube

Pentisteriruncicantic 6-cube
Type	uniform 6-polytope
Schläfli symbol	t0,1,2,3,4{3,32,1} h2,3,4,5{4,34}
Coxeter-Dynkin diagram	=
5-faces
4-faces
Cells
Faces
Edges	34560
Vertices	11520
Vertex figure
Coxeter groups	D6, [33,1,1]
Properties	convex

The pentisteriruncicantic 6-cube, , has half of the vertices of a pentisteriruncicantellated 6-cube (pentisteriruncicantitruncated 6-orthoplex), .

Alternate names

• Steriruncicantitruncated 6-demicube/demihexeract
• Great cellated hemihexeract (Acronym: gochax) (Jonathan Bowers)^[8]

Cartesian coordinates

The Cartesian coordinates for the vertices, centered at the origin are coordinate permutations:

(±1,±1,±3,±3,±5,±7)

with an odd number of plus signs.

Images

orthographic projections

Coxeter plane	B6
Graph
Dihedral symmetry	[12/2]
Coxeter plane	D6	D5
Graph
Dihedral symmetry	[10]	[8]
Coxeter plane	D4	D3
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Related polytopes

There are 47 uniform polytopes with D₆ symmetry, 31 are shared by the B₆ symmetry, and 16 are unique:

D6 polytopes
h{4,34}	h2{4,34}	h3{4,34}	h4{4,34}	h5{4,34}	h2,3{4,34}	h2,4{4,34}	h2,5{4,34}
h3,4{4,34}	h3,5{4,34}	h4,5{4,34}	h2,3,4{4,34}	h2,3,5{4,34}	h2,4,5{4,34}	h3,4,5{4,34}	h2,3,4,5{4,34}